
- •Р астяжение, сжатие
- •1.1. Построение эпюры продольных сил.
- •1.2. Вычисление размеров поперечного сечения.
- •1.3. Определение перемещения свободного конца стержня.
- •Г еометрические характеристики плоских сечений
- •2.1. Нахождение центра тяжести составного сечения.
- •2.2. Нахождение момента инерции относительно центральных осей.
- •Р асчет прочно-плотного заклепочного шва
- •3.1 Определение толщины δ стенки котла.
- •3.2. Определение диаметра d заклепок и шага заклепочного шва p.
- •3.3. Проверочный расчет.
- •3 .4. Расчет параметров шва.
- •3 .5. Определение напряжений на наклонной площадке.
- •К ручение
- •4.1. Построение эпюры крутящих моментов.
- •4.2. Вычисление диаметра вала.
- •4.3. Построение эпюры углов поворота.
- •5.1. Построение эпюр поперечных сил и изгибающих моментов.
- •5.2. Нахождение размера сечения балки.
- •5.3. Проверка сечения по касательным напряжениям.
- •5.4. Построение эпюр напряжений.
- •5.5. Определение прогиба.
- •П роектный расчет вала при совместном действии кручения и изгиба
- •Список использованной литературы
2.1. Нахождение центра тяжести составного сечения.
Выберем произвольную систему координат x0y0 (пусть она совпадает с собственными осями бруса), относительно которой будем искать центр тяжести сечения. Координаты центра тяжести определяются по формулам
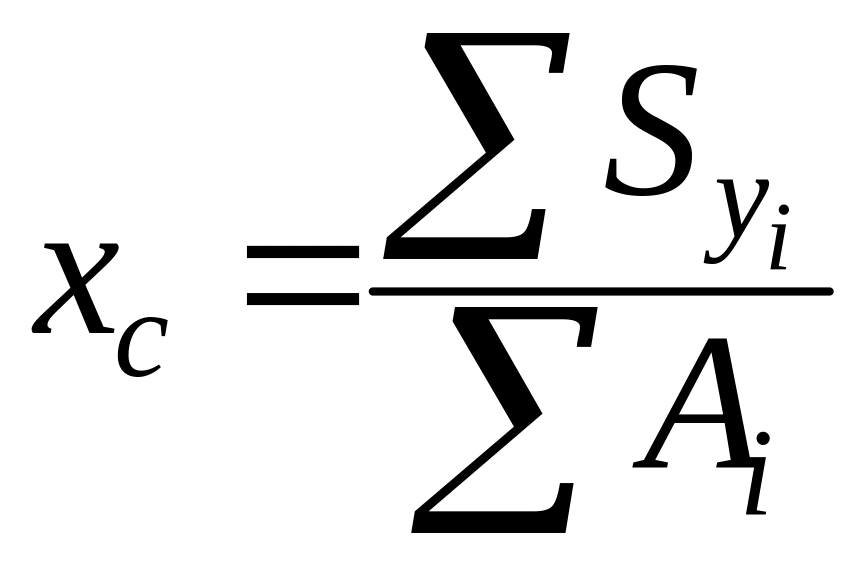 ;
; 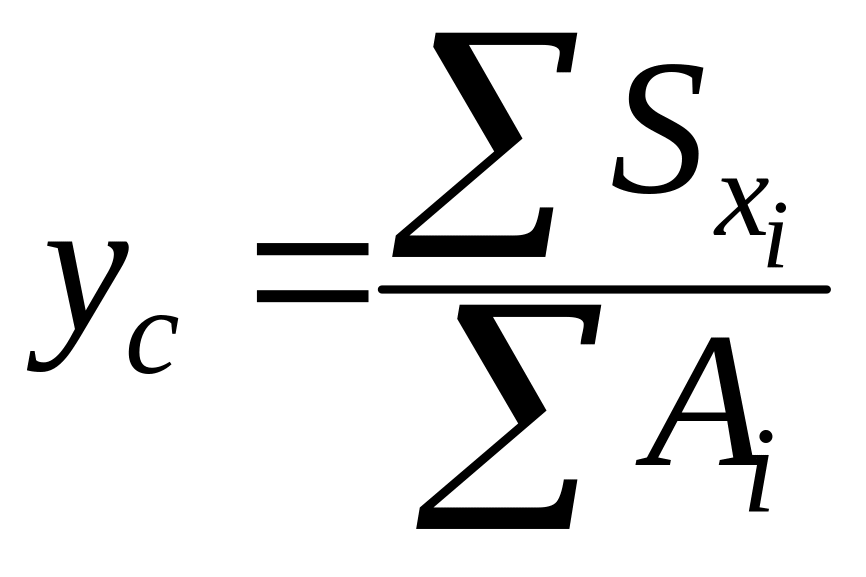 ,
,
где
![]() ,
,
![]() – статические моменты относительно
осей x0
и y0
соответственно каждой фигуры, входящей
в сечение;
– статические моменты относительно
осей x0
и y0
соответственно каждой фигуры, входящей
в сечение;
![]() –
площадь отдельной фигуры.
–
площадь отдельной фигуры.
Площади сечений неравнобокого уголка, швеллера и двутавра взяты из таблиц сортаментов ([3], с.342-354, табл. 1, 2, 4).
Таблица 2.2
Номер фигуры |
Тип сечения |
А, см2 |
|
|
1. |
Неравнобокий уголок |
22,2 |
444 |
146 |
2. |
Швеллер |
13,3 |
304 |
31,2 |
3. |
Двутавр |
14,7 |
350 |
27,9 |
Длина бруса
![]() мм.
мм.
Площадь сечения бруса найдем по формуле
![]() см2
см2 .
.
Статические моменты фигуры вычисляются по формулам
![]() ;
; ![]() ,
,
где А
– площадь фигуры;
![]() ,
,
![]() – расстояния от центра тяжести фигуры
до осей x0
и y0
соответственно.
– расстояния от центра тяжести фигуры
до осей x0
и y0
соответственно.
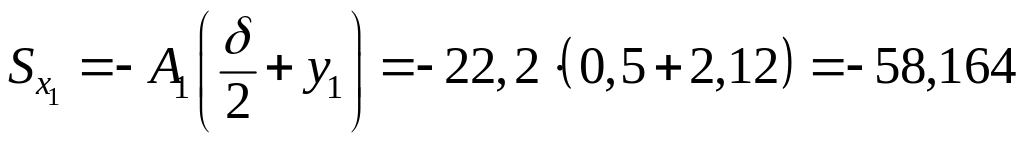 см3;
см3;
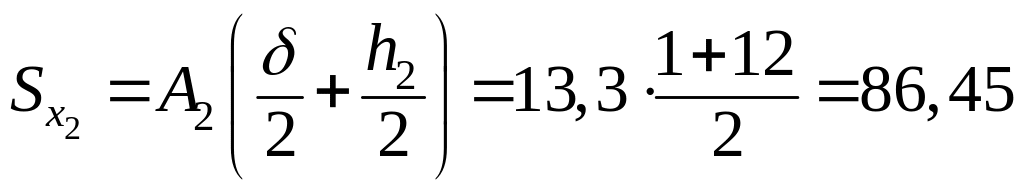 см3;
см3;
 см3;
см3;
![]() см3;
см3;

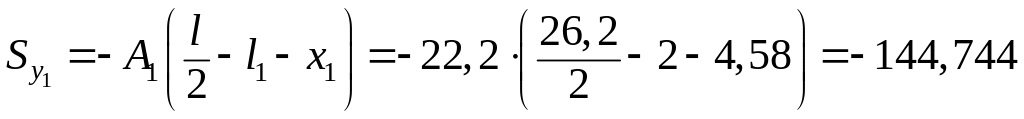 см3;
см3;
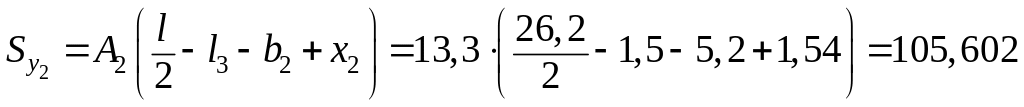 см3;
см3;
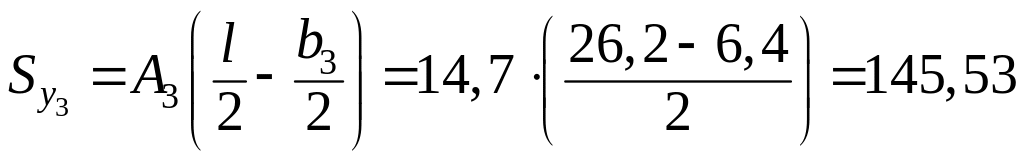 см3;
см3;
![]() см3.
см3.
Таким образом, координаты центра тяжести равны:
![]() см;
см;
![]() см.
см.
2.2. Нахождение момента инерции относительно центральных осей.
Вычислим моменты инерции относительно осей, проходящих через центр тяжести сечения. Введем центральные оси составного сечения x и y. Согласно теореме о переносе осей (теореме Гюйгенса-Штейнера) момент инерции каждой фигуры относительно центральной оси будет складываться из собственного и переносного моментов инерции:
![]() ;
; ![]() ,
,
где
![]() ,
,
![]() – моменты инерции относительно
собственных осей фигуры; А
– площадь фигуры; a,
b
– расстояние между собственной осью
фигуры и центральной осью составного
сечения (соответственно x
и y).
– моменты инерции относительно
собственных осей фигуры; А
– площадь фигуры; a,
b
– расстояние между собственной осью
фигуры и центральной осью составного
сечения (соответственно x
и y).
Собственные моменты инерции неравнобокого уголка, швеллера и двутавра взяты по сортаменту (см. табл. 2.2).
Собственные моменты инерции бруса определяются по формулам
![]() см4;
см4;
![]() см4.
см4.
Таким образом, моменты инерции фигур в составе сечения относительно центральных осей составного сечения будут иметь вид:
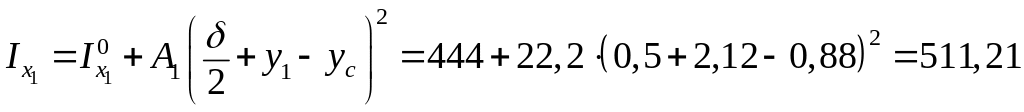
 см4;
см4;
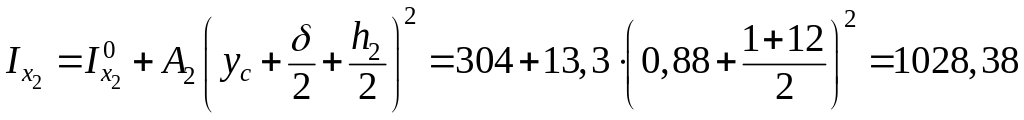 см4;
см4;
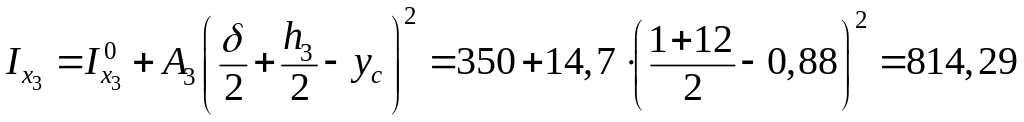 см4;
см4;
![]() см4;
см4;
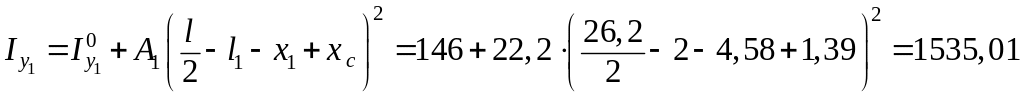
 см4;
см4;
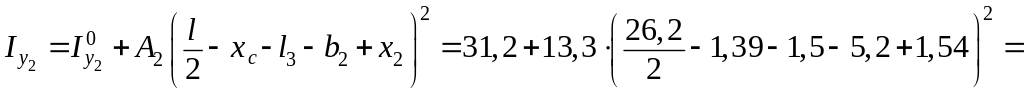
![]() см4;
см4;
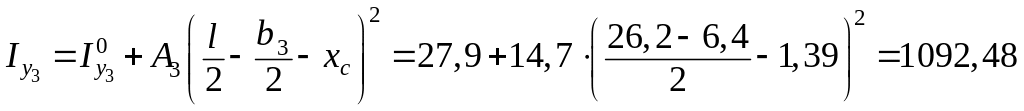 см4;
см4;
![]() см4;
см4;
Момент инерции составного сечения относительно оси x:
![]() см4;
см4;
относительно оси y:
![]() см4.
см4.
Задача 3
Р асчет прочно-плотного заклепочного шва
Рассчитать продольный прочно-плотный шов для котла с внутренним давлением q, диаметром D, выполненного из стали, а также определить напряжения на наклонной площадке элемента стенки котла. Исходные данные указаны в табл. 3.1.
Таблица 3.1
№ п/п |
Диаметр котла D, м |
Температура нагрева стенки котла, град. |
Внутреннее давление в котле q, МПа |
Материал листов для стенок котла, сталь ГОСТ 19903-74 |
Угол наклона площадки, град. |
Вид элемента |
14 |
1,2 |
180 |
0,8 |
Сталь 15пс |
15 |
|
Рис. 3.1.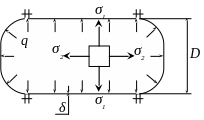
Решение
3.1 Определение толщины δ стенки котла.
Условие прочности на растяжение для тонкостенного сосуда имеет вид:
![]() ,
,
где ![]() – допускаемое напряжение при растяжении;
– допускаемое напряжение при растяжении;
[S] – допускаемый коэффициент прочности шва.
Температура нагрева стенки котла 180°С < 250°С, поэтому вычислим по формуле:
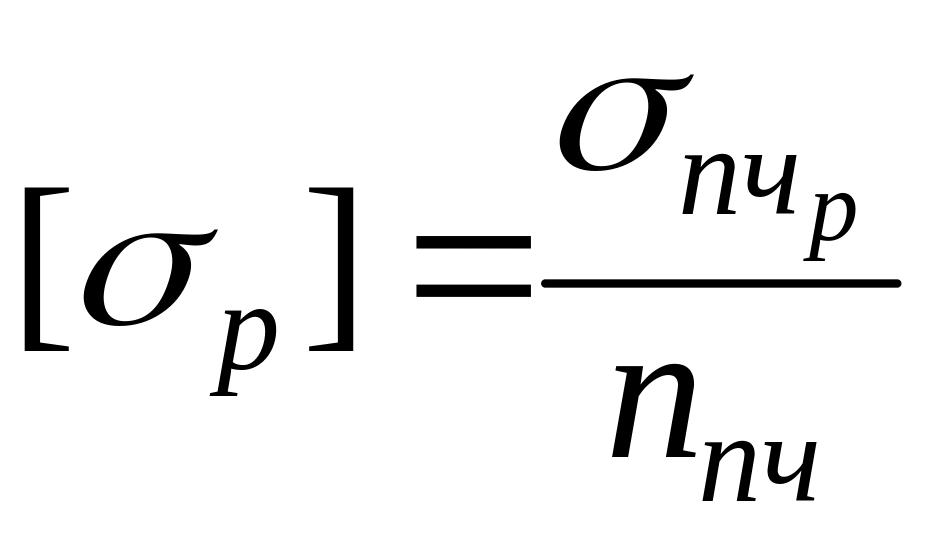 ,
,
где ![]() – предел прочности при растяжении
материала листов стенки котла;
– предел прочности при растяжении
материала листов стенки котла;
![]() – коэффициент запаса прочности,
соответствующий
;
– коэффициент запаса прочности,
соответствующий
;
![]() .
.
Для стали марки
15пс
![]() МПа ([2], с.
50).
МПа ([2], с.
50).
Исходя из соотношения
![]() МПа∙м, примем тип шва – двухрядный
стыковой. Допускаемый коэффициент
прочности для такого типа шва ([м.у.],
табл. 2.1):
МПа∙м, примем тип шва – двухрядный
стыковой. Допускаемый коэффициент
прочности для такого типа шва ([м.у.],
табл. 2.1):
![]() .
.
В качестве
максимального напряжения примем
![]() как наиболее опасное:
как наиболее опасное:
![]() .
.
Таким образом, условие прочности примет вид:
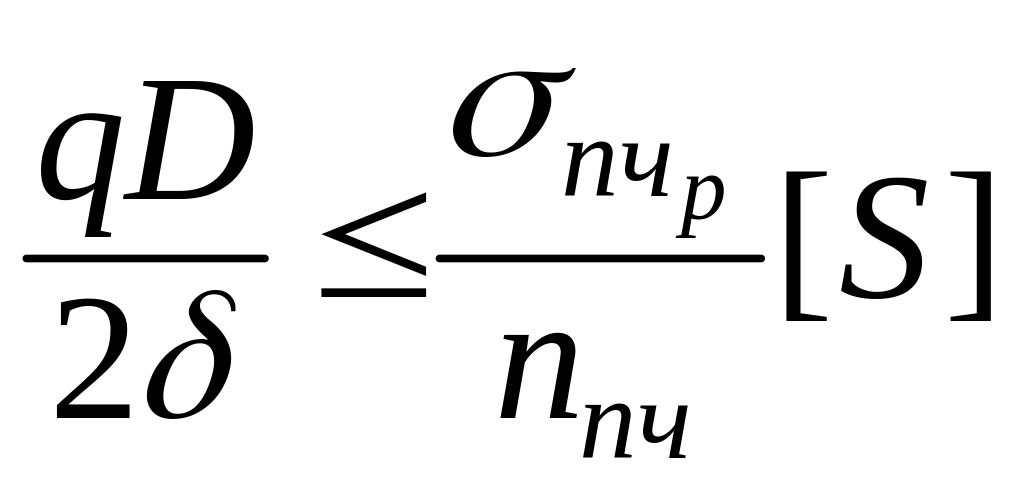 ;
; 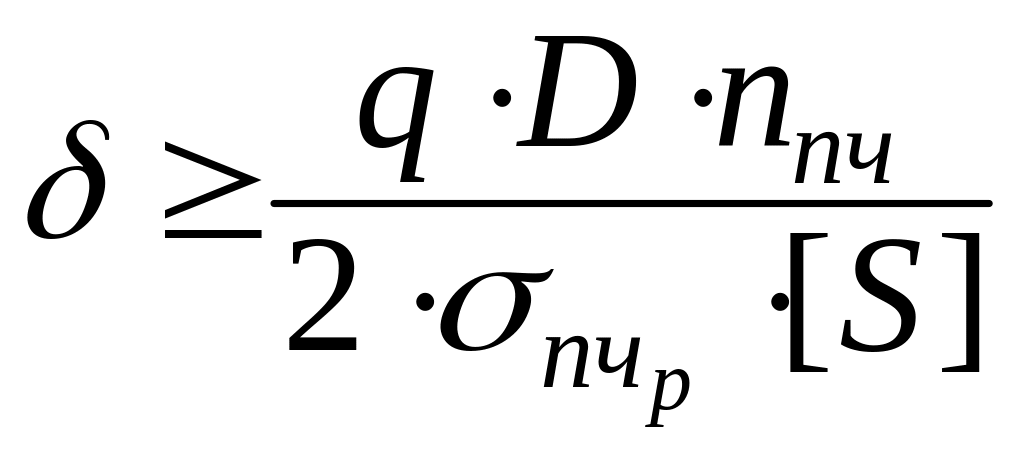 .
.

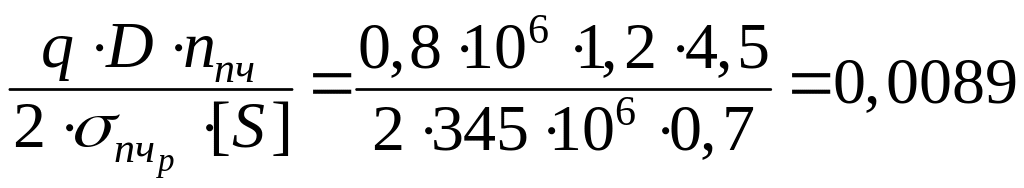 м
м
![]() мм.
мм.
С учетом добавки
на коррозию металла
![]() мм принимаем значение:
мм принимаем значение:
![]() мм.
мм.
