20.Частотные характеристики статических систем.
Системы в которых в своей структуре не содержится последовательно присоединенного интегрирующего звена называют статическими. Примером статических систем служат последовательно соединенные звенья с передаточными функциями:
Система в структуре которой имеется последовательное соединённое интегрирующее звено называется астатической.
Если
к данному примеру прибавить 
В
знаменателе появляется множитель в
компл. переменной «р». Последовательное
присоединение еще одного интегр. Звена
изменит множитель на «
».
Пример.
Передаточная функция неизменяемой части САР:
Переведем
передаточную функцию разомкнутой
системы в комплексные числа, то есть
выделим действительную и мнимую части.
– действительная часть:
– мнимая часть:
.
Амплитудно-частотная характеристика описывается выражением:
.
Рисунок 2 - Амплитудно-частотная характеристика
Фазовая частотная характеристика описывается выражением:
.
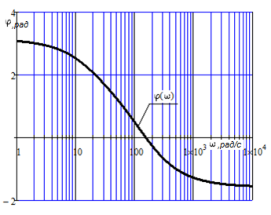
Рисунок 3 - Фазовая частотная характеристика
21. Применение изодромных устройств
Существует путь повышения порядка ас-татизма системы без заметного или недопустимого ухудшения ее запаса устойчивости. Этот путь заключается в применении изодромных устройств, например таких, как изображенные па рис. 4.19. Структурная схема системы при введении изодром-ного устройства изображена па рис. 9.4. Передаточная функция изодромного устройства может быть представлена в виде
22.Чх систем с обратной связью
Обратная связь может быть как положительной, так и отрицательной. Отрицательная обратная связь (ООС) действует в сторону уменьшения отклонений текущих значений координат объекта от их предшествующих значений, а положительная обратная связь (ПОС) действует в сторону увеличения. Следовательно, ООС позволяет строить наиболее точные САУ, так как несёт в себе информацию обо всех изменениях регулируемой величины; ПОС служит для изменения внутренних свойств отдельных звеньев САУ.
Соединение обратной связью
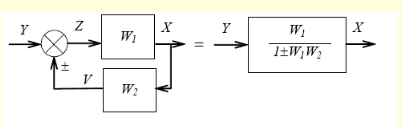
Если задана передаточная Функция W(S), то путём подставки S=jw получаем частотную передаточную функцию W (jw), которая является комплексным выражением т.е.
А(w) – вещественная составляющая
К(w) – мнимая составляющая.
Частотная передаточная функция может быть представлена в показательной форме
Функция М(w), представленная при изменении частоты от 0 до Ґ получило название амплитудной частотной характеристики (АЧХ).Функция j(w), представленная при изменении частоты от 0 до Ґ называется фазовой частотной характеристикой (ФЧХ). Для анализа поведения системы в большом диапазоне частот удобно в качестве аргумента частотных характеристик рассматривать не частоту ω, а ее десятичный логарифм ω 10 log.
23. Типовые временные характеристики
Для оценки динамических свойств системы и отдельных звеньев принято исследовать их реакцию на типовые входные воздействия, которые наиболее полно отражают особенности реальных возмущений. Во-первых, это позволяет сравнивать отдельные элементы между собой с точки зрения их динамических свойств. Во-вторых, зная реакцию системы на типовые воздействия, можно судить о том, как она будет вести себя при сложных изменениях входной величины.
Наиболее распространенными типовыми воздействиями являются: ступенчатое, импульсное и рамповое воздействия. Любой сигнал u(t), имеющий сложную форму, можно разложить на сумму типовых воздействий ui(t) и исследовать реакцию системы на каждую из составляющих, а затем, пользуясь принципом суперпозиции, получить результирующее изменение выходной величины y(t)суммируя полученные таким образом составляющие выходного сигнала yi(t).
Единичное ступенчатое воздействие (функция Хевисайда).
Аналитическое выражение x=1(τ). Его изображение L[1(τ)] = 1/s
Единичное импульсное воздействие (дельта-функция Дирака).
Аналитическое выражение x = δ(τ). Его изображение L[δ(τ)] = 1
Единичное рамповое воздействие (воздействие с постоянной скоростью). Аналитическое выражение x = τ·1(τ). Его изображение L[τ·1(τ)] = 1/s2
Изменения во времени выходной величины звена (системы) называют
временными характеристиками звена (системы) или кривыми отклика.
