16.Соединения динамических звеньев.

Поскольку исследуемый объект в целях упрощения анализа функционирования разбит нами на звенья, то после определения передаточных функций для каждого звена встает задача объединения их в одну передаточную функцию объекта. Вид передаточной функции объекта зависит от последовательности соединения звеньев:

1) Последовательное соединение.

W_об = W₁^.W₂^.W₃…

При последовательном соединении звеньев их передаточные функции перемножаются.

2) Параллельное соединение.

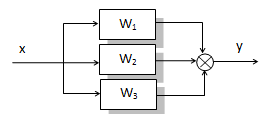
W_об = W₁ + W₂ + W₃ + …

При параллельном соединении звеньевих передаточные функции складываются.

3) Обратная связь

Передаточная функция по заданию (х):

«+» соответствует отрицательной ОС,

«-» - положительной.

Для определения передаточных функций объектов, имеющих более сложные соединения звеньев, используют либо последовательное укрупнение схемы, либо преобразуют по формуле Мезона.

17.Характеристический полином и характеристическое уравнение.

Поскольку передаточная функция разомкнутой системы является в общем случае дробно-рациональной функцией вида W_ = , то передаточные функции замкнутой системы могут быть преобразованы:

гдеD = A + B.

Как видно, эти передаточные функции отличаются только выражениями числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как D_з(s) = A(s) + B(s), в то время как выражение, находящееся в знаменателе передаточной функции разомкнутой системы W_, называется характеристическим выражением разомкнутой системыА(s).

19.Частотные характеристики интегрирующих систем.

Идеальное интегрирующее звено.

Звено описывается дифференциальным уравнением:

.

Его кривая разгона:

,

передаточная функция:

,

амплитудно-фазовая характеристика:

,

амплитудно-частотная характеристика:

,

фазочастотная характеристика:

.

На рис. 47 и 48 приведены временные, а на рис. 49, 50, 51 – частотные характеристики идеального интегрирующего звена.

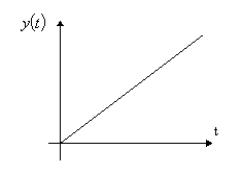
Рис.47. Кривая разгона

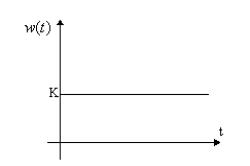
Рис.48. Импульсная переходная функция

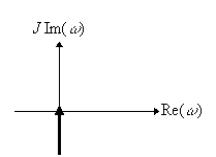
Рис. 49. Амплитудно-фазовая характеристика

Рис. 50. Амплитудно-частотная характеристика

Рис. 51. Фазочастотная характеристика

Реальное интегрирующее звено

Звено описывается дифференциальным уравнением:

.

Его кривая разгона:

,

импульсная переходная функция:

,

передаточная функция:

,

амплитудно-фазовая характеристика:

,

амплитудно-частотная характеристика:

,

фазочастотная характеристика:

.

На рис. 53, 54, 55, 56, 57 приведены соответственно кривая разгона, импульсная переходная функция, АФХ, АЧХ и ФЧХ идеального интегрирующего звена.

Примером такого звена является двигатель (рис. 58).

Уравнение двигателя, приведенного на рис. 58, можно записать в виде:

,

где T– постоянная времени двигателя,

k – коэффициент передачи.

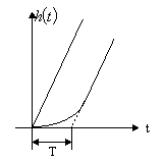
Рис. 53. Кривая разгона

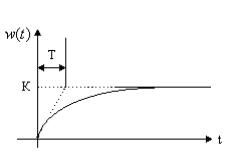
Рис. 54. Импульсная переходная функция

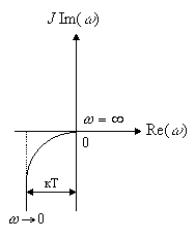
Рис. 55. Амплитудно-фазовая характеристика

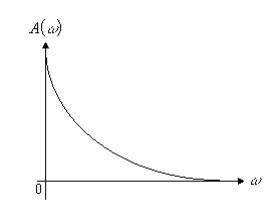
Рис. 56. Амплитудно-частотная характеристика

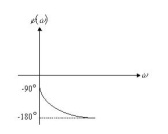
Рис. 57. Фазочастотная характеристика

Рис. 58. Реальное интегрирующее звено:

X – управляющее воздействие (например, подводимое напряжение  в двигателе), Y – угол поворота вала двигателя

где  – коэффициент пропорциональности между управляющим воздействием X и выдающим моментом M;

Y – приведенный к валу двигателя суммарный момент инерции;

 – соответственно пусковой момент и скорость холостого хода двигателя при некотором значении управляющего воздействия.