46. Выпуклые множества, выпуклые и вогнутые функции. Теорема Куна-Таккера.

Определение: Функция , заданная на выпуклом множестве , называется выпуклой, если для любых двух точек и из и любо­го выполняется соотношение

(49.1)

Определение: Функция , заданная на выпуклом множестве , называется вогнутой, если для любых двух точек и из и любо­го выполняется соотношение

(49.2)

Если неравенства (49.1) и (49.2) считать строгими и они выполняются при , то функция является строго выпуклой (строго вогнутой). Выпуклость и вогнутость функций определяется только относительно выпуклых множеств.

Если 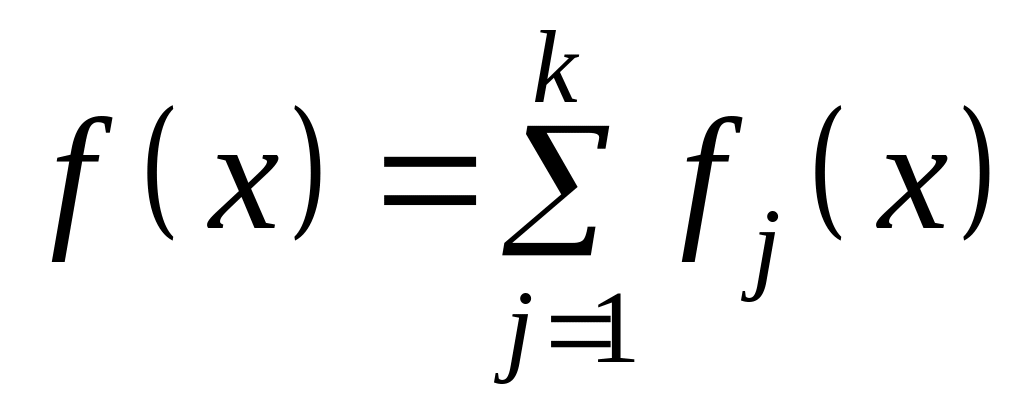, где , - выпуклые (вогнутые) функции на некотором выпуклом множестве , то функция - также выпуклая (вогнутая) на .

Основные свойства выпуклых и вогнутых функций:

1. Множество точек минимума выпуклой функции, заданной на выпук­лом множестве, выпукло.

2. Пусть - выпуклая функция, заданная на замкнутом выпуклом множестве . Тогда локальный минимум на является и глобальным.

3. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.

4. Если - строго выпуклая функция, то ее глобальный минимум на выпуклом множестве достигается в единственной точке.

5. Пусть функция - выпуклая функция, заданная на выпуклом множестве , и, кроме того, она непрерывна вместе со своими частными производными первого порядка во всех внутренних точках . Пусть - точка, в которой . Тогда в точке достигается локальный минимум, совпадающий с глобальным минимумом.

6. Множество точек глобальных (следовательно, и локальных) мини­мумов выпуклой функции , заданной на ограниченном замкнутом вы­пуклом множестве , включает хотя бы одну крайнюю точку; если множест­во локальных минимумов включает в себя хотя бы одну внутреннюю точку множества , то является функцией-константой.

Рассмотрим задачу нелинейного программирования:

(49.3)

при ограничениях

, (49.4)

(49.5)

Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функ­ций и , разработаны эффективные методы их решения.

Говорят, что множество допустимых решений задачи (49.3) - (49.5) удов­летворяет условию регулярности, или условию Слейтера, если существует, по крайней мере, одна точка , принадлежащая области допустимых ре­шений такая, что .

Задача (49.3) - (49.5) называется задачей выпуклого программирования, если функция является во­гнутой (выпуклой), а функции - выпуклыми.

Функцией Лагранжа задачи выпуклого программирования (49.3) - (49.5) называется функция:

, (49.6)

где - множители Лагранжа.

Точка называется седловой точкой функции Лагранжа, если

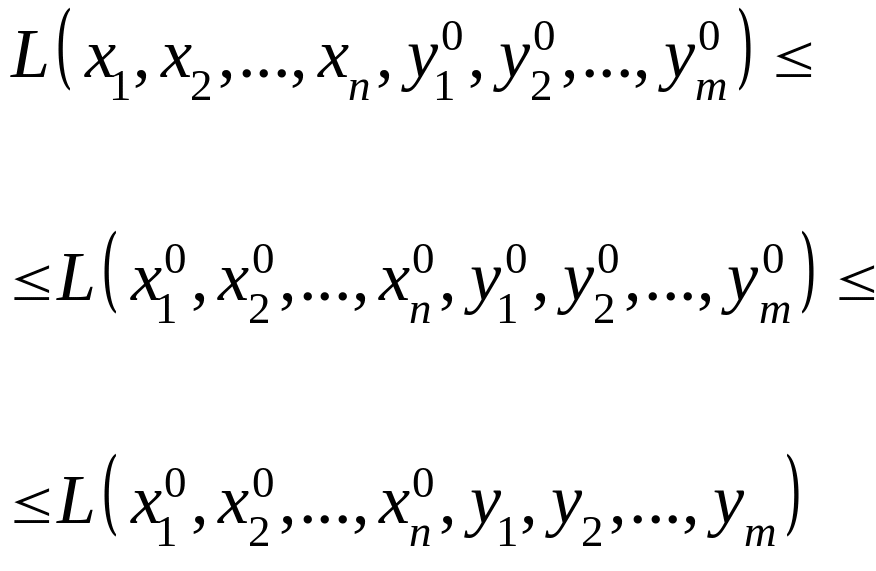(49.7)

для всех и .

Теорема (Куна - Таккера): Для задачи выпуклого програм­мирования (49.3) - (49.5), множество допустимых решений которой обладает свойством регулярности, является опти­мальным решением тогда и только тогда, когда существует такой вектор , , что - седловая точка функции Лагранжа.

_{На доп. вопрос: Что есть свойство регулярности?}