46. Множители Лагранжа.

Другой способ определения условного экстремума начинается с построения вспомогательной функции Лагранжа, которая в области допустимых решений достигает максимума для тех же значений переменных , что и целевая функция .

Пусть решается задача определения условного экстремума функции при ограничениях , .

Составим функцию: , (47.1) которая называется функцией Лагранжа. Где - постоянные множители Лагранжа.

Отметим, что множителям Лагранжа можно придать экономический смысл. Если — доход, соответствующий плану , а функция — издержки i-го ресурса, соответствующие этому плану, то , — цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (маргинальная оценка – равновесная, действительная цена).

функция n + m переменных .

Определение стационарных точек этой функции приводит к решению системы уравнений: (47.2)

Легко заметить, что , т.е. в (47.1) входят уравнения связи. Таким образом, задача нахождения условного экстремума функции сводится к нахождению локального экстремума функции .

Таким образом, определение экстремальных точек методом Лагранжа включает следующие этапы:

1. Составляют функцию Лагранжа.

2. Находят частные производные от функции Лагранжа и приравнивают их нулю.

3. Решая систему уравнений (47.2), находят точки, в которых целевая функция задачи может иметь экстремум.

4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычисляют значение функции в этих точках.

Пример.  Определить точки экстремума , если уравнение связи .

Решение.  

Составим .

линейная система уравнений. Применяя метод Крамера, получим: и т.  — т. условного максимума

Функция обладает условным экстремумом .

46. Задача о потребительском выборе.

В теории потребления предполагается, что потребитель всегда стремится максимизировать свою полезность и ограничением для него является величина дохода , которую он может потратить на приобретение набора товаров.

В общем, задача потребительского выбора (задача рационального поведения потребителя на рынке) записывается следующим образом: найти такой потребительский набор , который максимизирует его функцию полезности при заданном бюджетном ограничении.

_{Задачу потребительского выбора (для n-мерного набора) можно записать в виде:}

, (48.1)

Задача потребительского выбора (для случая набора из двух товаров): найти такой набор , для которого

, (48.2)

.

Решение:

Рис. 48.1

Поиск оптимального набора графически можно изобразить как последовательный переход на кривые безразличия более высокого уровня полезности (см. рис. 48.1) вправо и вверх до тех пор, пока эти кривые имеют общие точки с бюджетным множеством. Из рисунка следует, что искомая точка лежит на границе G, т.е. на прямой .

Таким образом, задача потребительского выбора сводится к задаче на условный экстремум функций двух переменных: найти точку , для которой: .

Второе уравнение выражения называется уравнением связи.

Для решения задачи используем метод Лагранжа. Составим функцию Лагранжа:

, (48.3)

где l - множитель Лагранжа.

Из (48.3) следует экономический смысл множителя Лагранжа: если цены и доход меняются в одно и то же число раз l, то функция полезности и решение задачи потребительского выбора не изменятся. Для нахождения максимума функции приравняем к нулю все три частные производные этой функции, получим систему уравнений:

(48.4)

Исключив из этих уравнений l, получим систему двух уравнений с неизвестными , : (48.5)

Из системы находится точка - решение задачи потребительского выбора.

Вернемся к n-мерному набору. Итак, точка лежит на границе G и удовлетворяет условию . Поэтому задача потребительского выбора формулируется аналогично в виде задачи на условный экстремум: при заданных функции , векторе и величине найти такую точку, что:

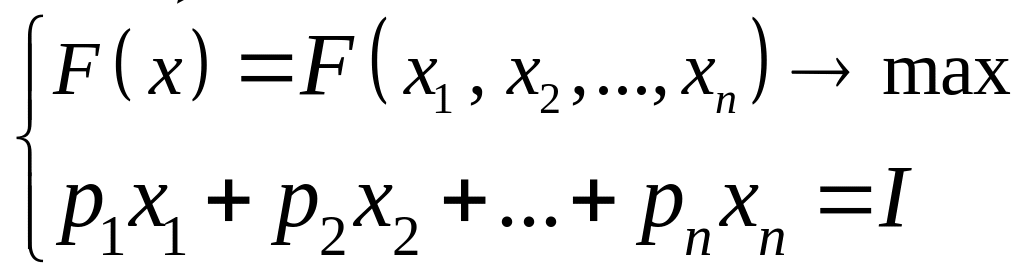(48.6)

Составим функцию Лагранжа:

(48.7)

Для нахождения максимума функции приравняем к нулю все частные производные этой функции, получим систему уравнений:

(48.8)

Исключив из уравнений множитель l, получим систему:

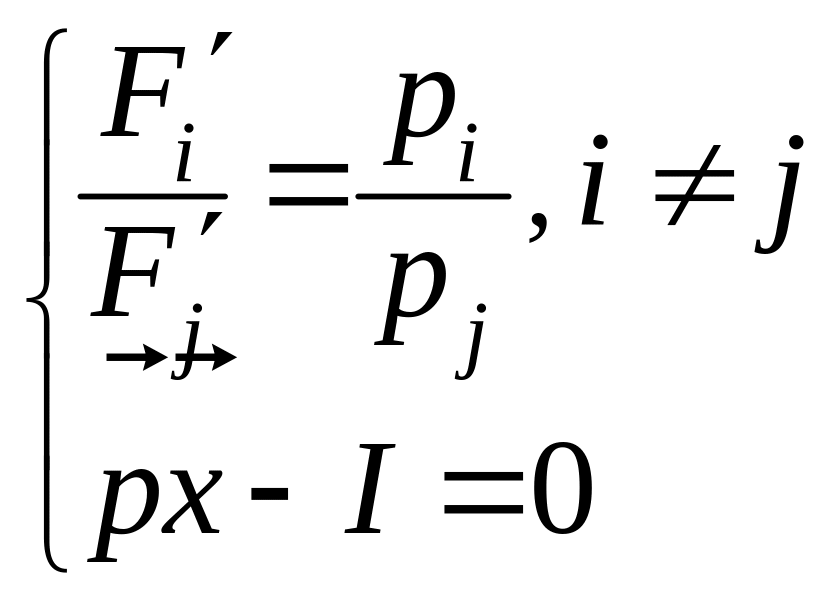(48.9)

Решение системы - точка условного экстремума. Это решение общей задачи потребительского выбора.

Точка называется точкой локального рыночного равновесия. Первое выражение системы (48.9) показывает, что отношение предельных полезностей продуктов в точке локального рыночного равновесия, или предельная норма замены i-го продукта j-м продуктом , равно отношению рыночных цен на эти продукты.