35. Двойственность задач линейного программирования. Таблица соответствий.

Определение: двойственная задача – это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной задачи, которая в этом случае называется прямой задачей линейного программирования.

Таблица 36.1

Прямая задача	Двойственная задача
Максимизация	Минимизация
Коэффициенты в целевой функции	Константы в правых частях ограничений
Константы в правых частях ограничений	Коэффициенты в целевой функции
i-я строка, составленная из коэффициентов при неизвестных в ограничениях	i-й столбец, составленный из коэффициентов при неизвестных в ограничениях
j-й столбец, составленный из коэффициентов при неизвестных в ограничениях	j-я строка, составленная из коэффициентов при неизвестных в ограничениях
i-е неравенство вида (этот знак неравенства согласован с целевой функцией на максимум)	i-я неотрицательная переменная:
i-е соотношение в виде равенства	i-я переменная , не имеющая ограничения в знаке
j-я неотрицательная переменная:	j-е неравенство вида (этот знак неравенства согласован с целевой функцией на минимум)
i-я переменная , не имеющая ограничения в знаке	i-е соотношение в виде равенства

Трудности в решении задач линейного программирования зависят не от количества переменных n, а от количества ограничений m, определяющих число итераций симплекс-метода. Поэтому, если прямая задача линейного программирования, еще не приведенная к стандартной форме, содержит большое количество ограничений (m>n), то в этом случае целесообразно перейти к двойственной задаче. Сформированная двойственная задача линейного программирования будет иметь m переменных и n ограничений, т.е. количество итераций при этом уменьшится.

Рассмотрим пару задач ЛП вида:

Таблица 36.2

Прямая задача (I)	Двойственная ей задача (II)
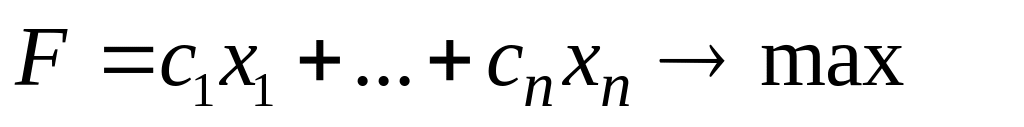
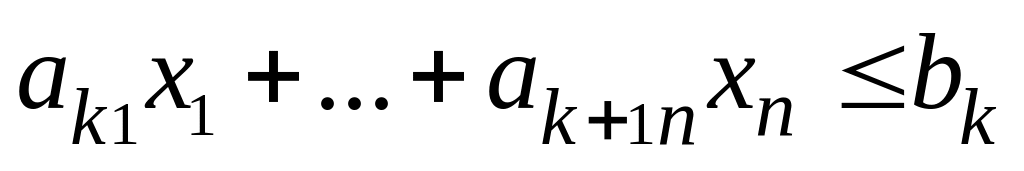
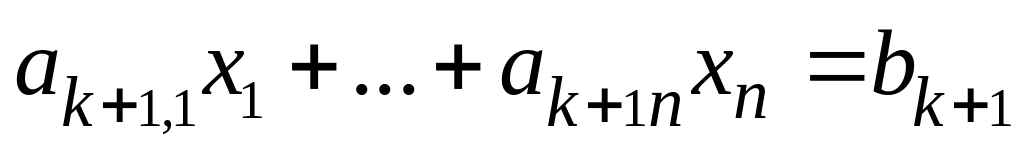
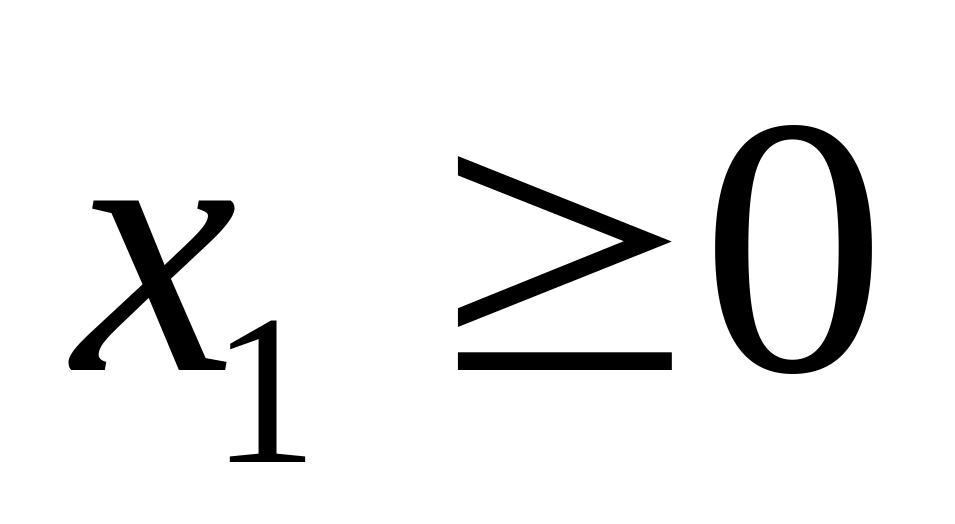
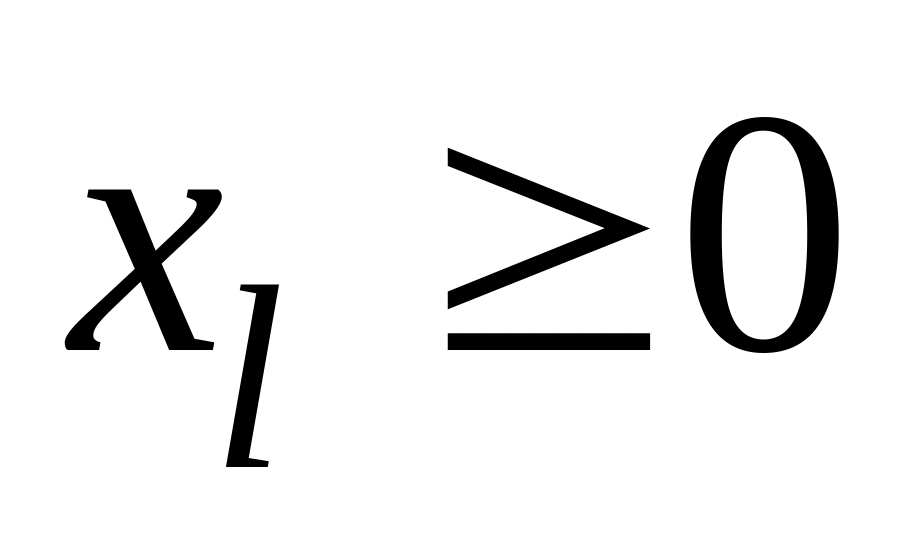
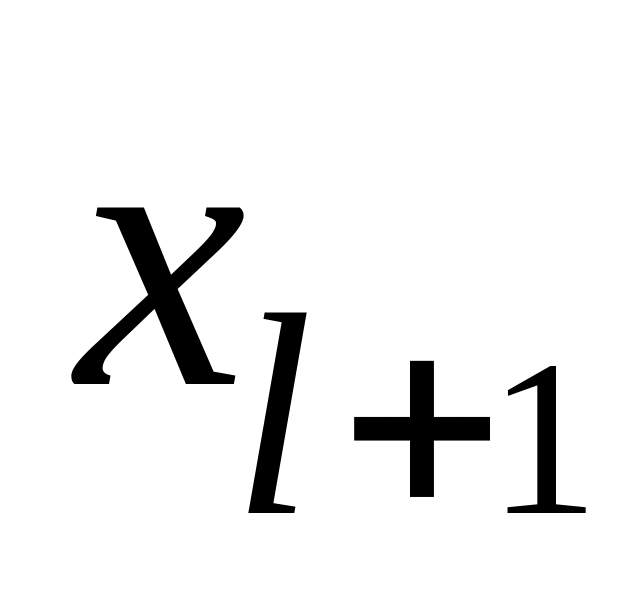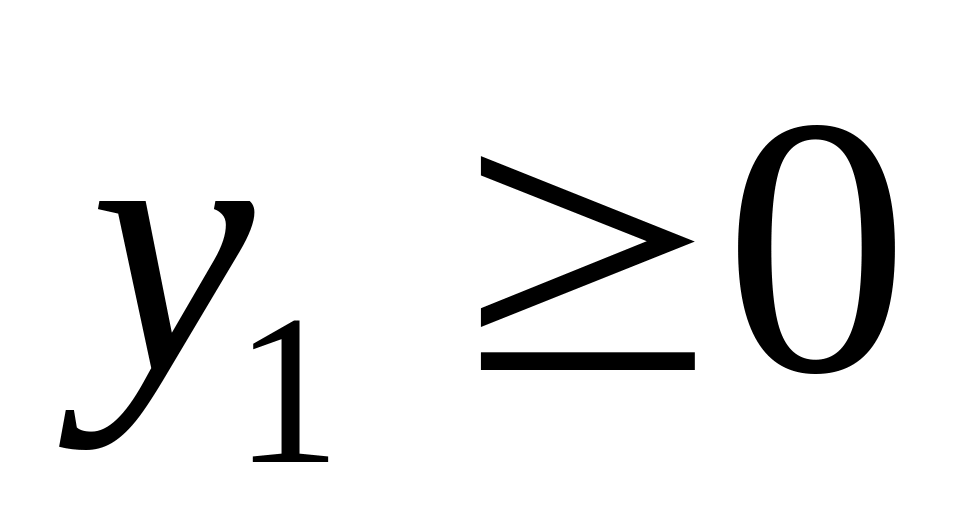
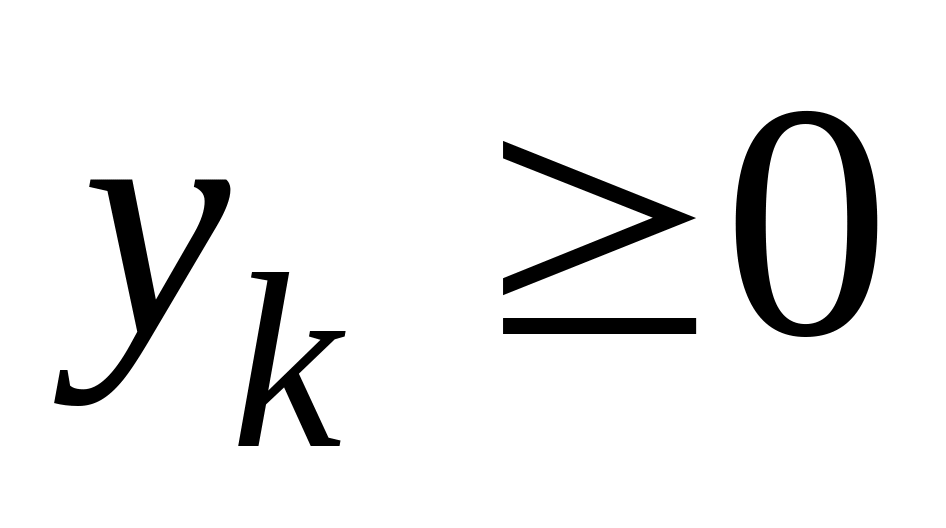
……………………… ……… - любое ……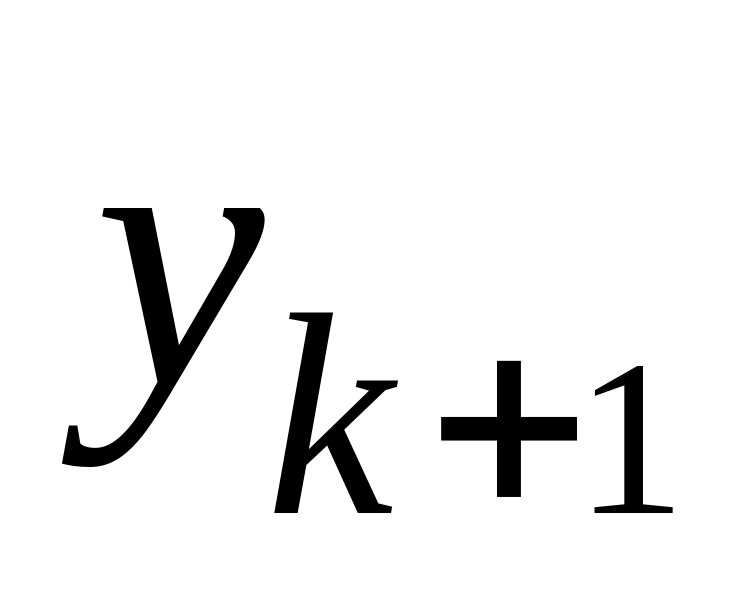.. - любое	……… - любое …….. - любое ……………………………..

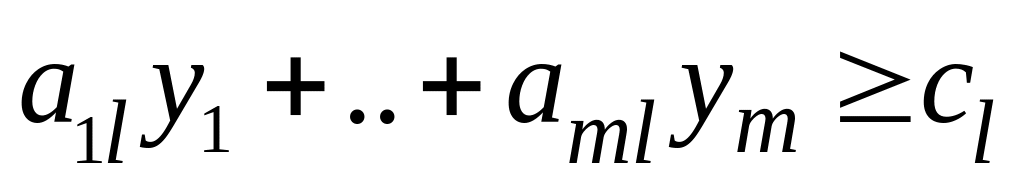
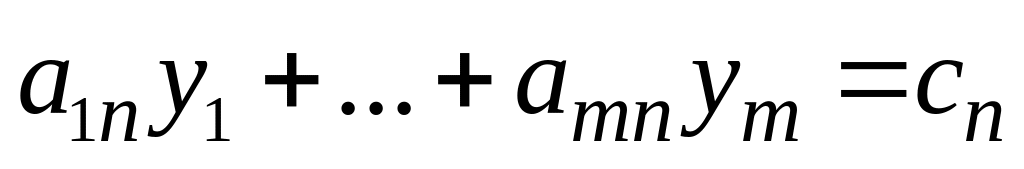
Задачу (I) называют прямой задачей ЛП, а (II) - двойственной. Ограничения задач (I) и (II), соответствующие друг другу, называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую - двойственной.

Грубо говоря, двойственная задача - это на 90⁰ повернутая исходная прямая задача. В этой связи полезно усвоить следующую схему соответствия.

Задача 36.1: построить двойственную задачу к следующей задаче ЛП:

Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях задачи с целевой функцией. Так как целевая функция минимизируется, то неравенства должны быть записаны с помощью знака Для этого второе неравенство умножим на -1:

Теперь, вводя двойственные переменные , , , запишем в соответствии с указанным правилом пару двойственных задач:

Таблица 36.3

Прямая задача (I)	Двойственная ей задача (II)
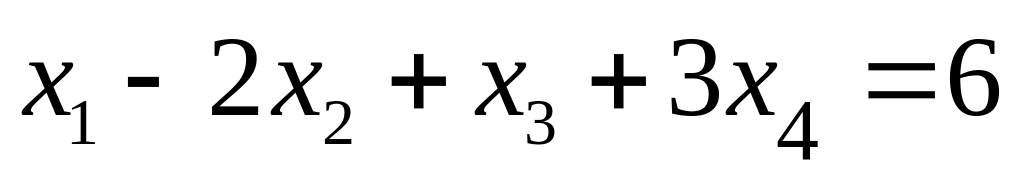
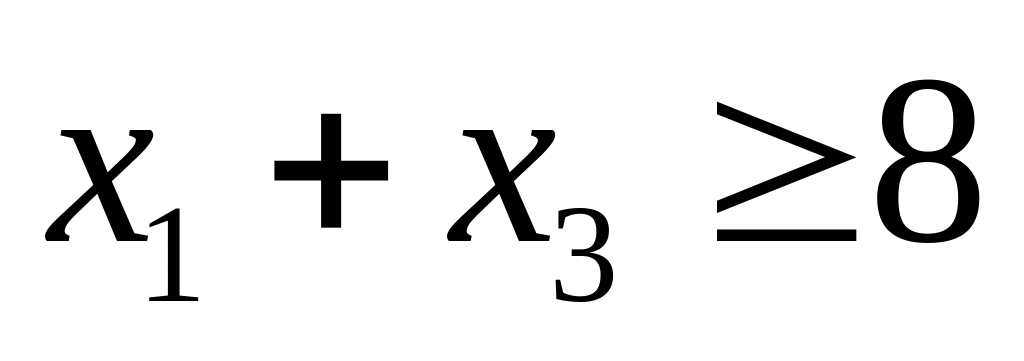
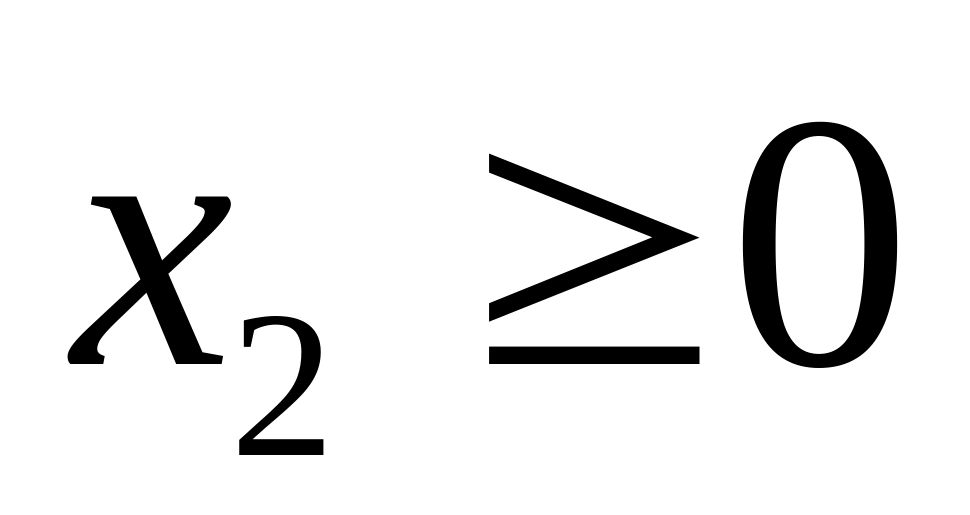
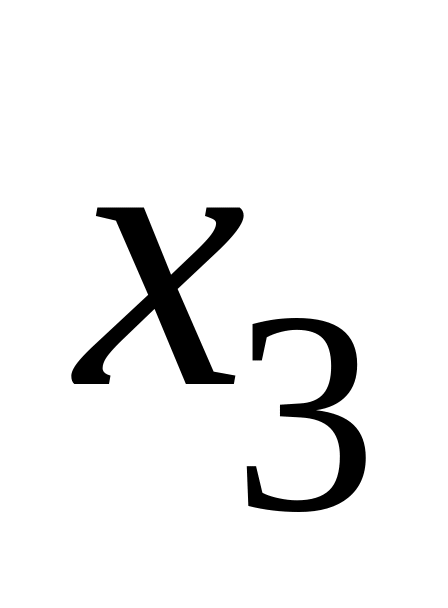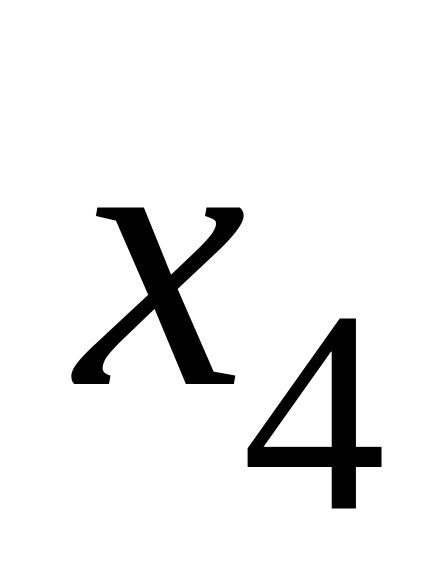- любое - любое	- любое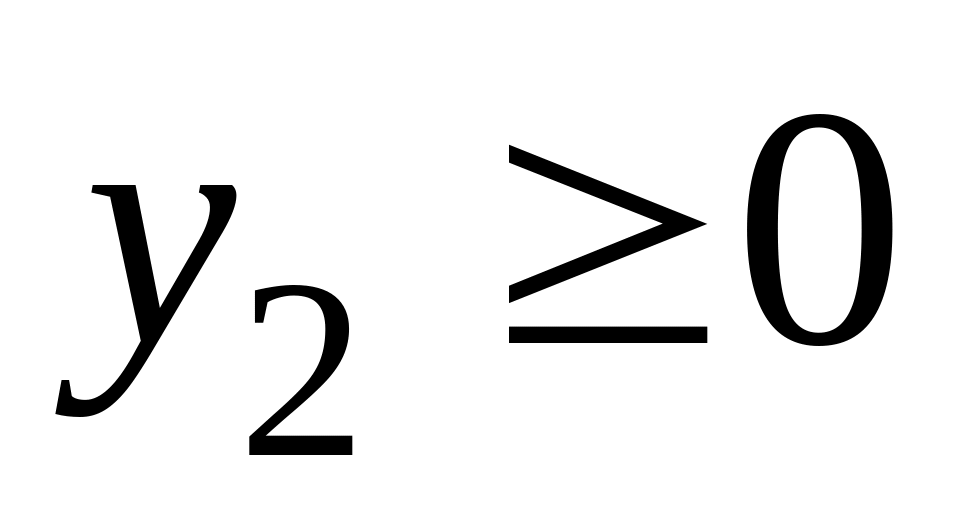

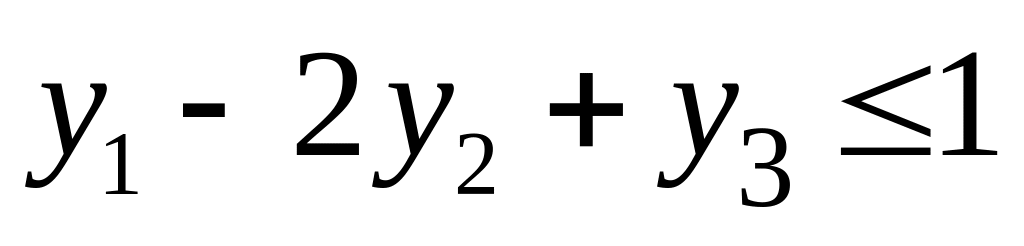
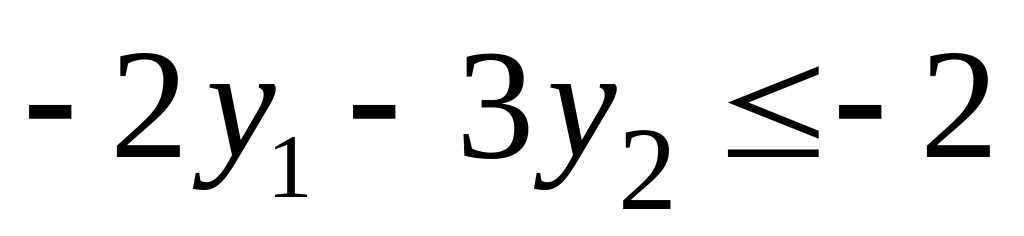
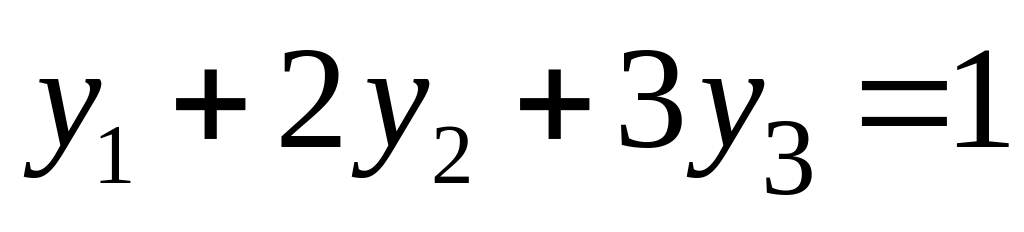
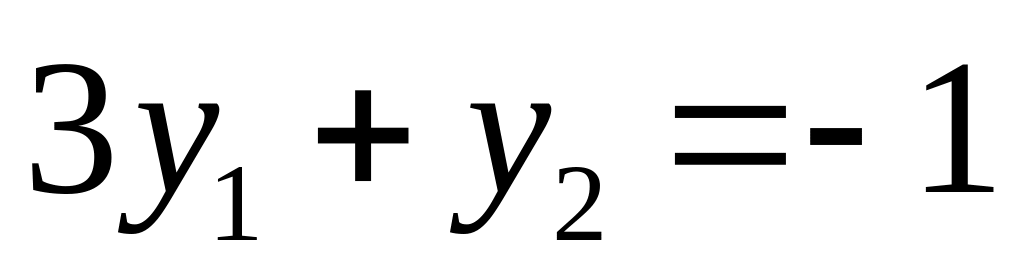
Итак, задача слева - исходная прямая задача, задача справа - двойственная к исходной задаче.