35. Локальный экстремум. Необходимое и достаточное условия.

Понятие экстремума вводится для случая, когда число переменных . Будем полагать, что функция дважды дифференцируема в точке , ( ) и в некоторой ее окрестности.

Определение: если для всех точек этой окрестности или , то говорят, что функция имеет экстремум в (соответственно максимум или минимум).

Определение: точка , в которой все частные производные функции равны нулю, называется стационарной точкой.

Необходимое условие экстремума: если в точке функция имеет экстремум, то частные производные функции в этой точке равны нулю: .

Следовательно, точки экстремума функции удовлетворяют системе уравнений:

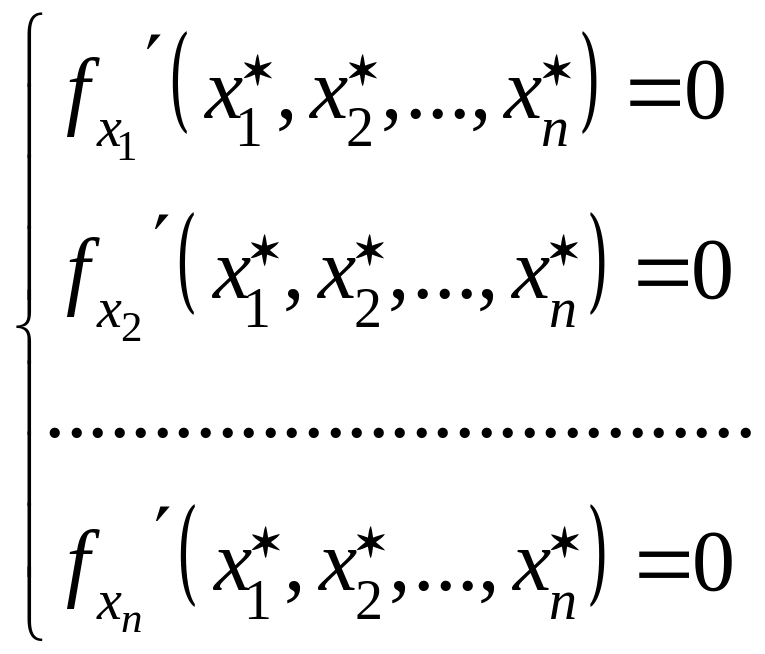(45.1)

Для получения достаточных условий следует определить в стационарной точке знак дифференциала второго порядка. Дифференциала второго порядка обозначается . Если найти частную производную по переменной х_j, то получим частную производную второго порядка по переменным х_i , х_j , которая обозначается .

В этом случае: 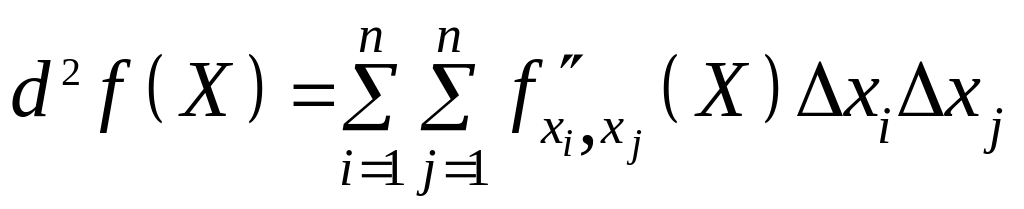. (45.2)

Достаточные условия экстремума (двух переменных):

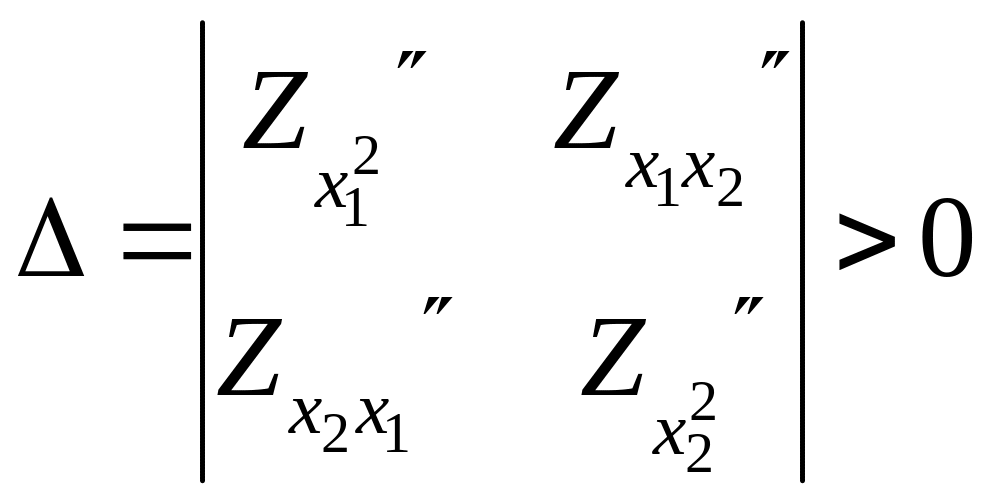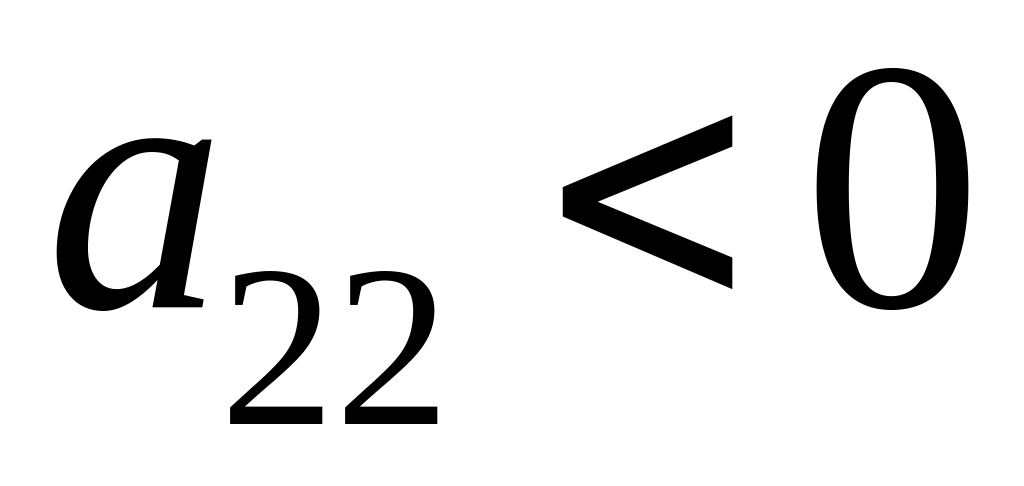• если и ( ), то в точке функция имеет максимум;

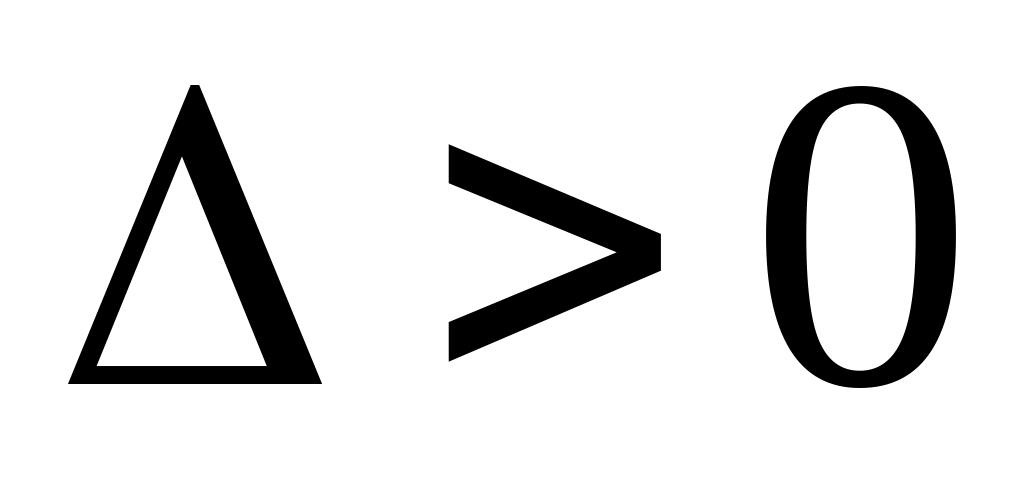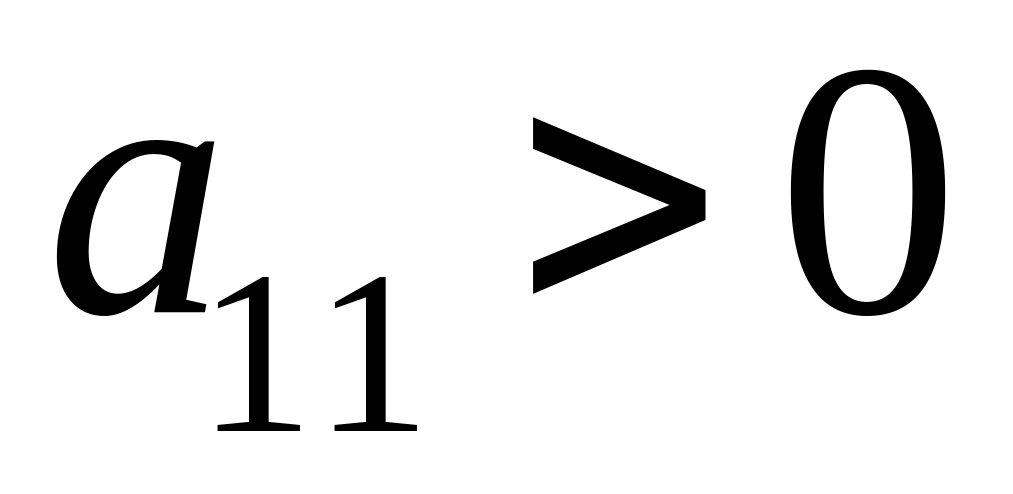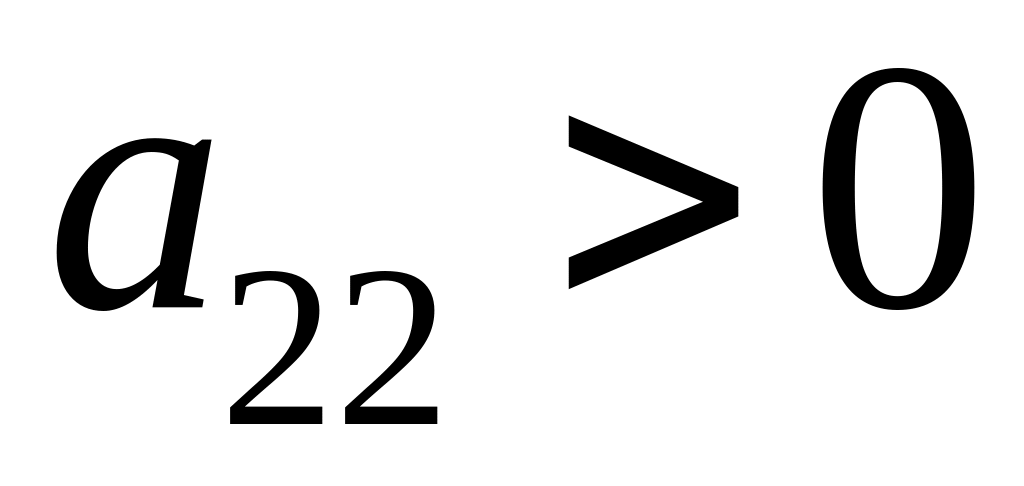• если и ( ), то в точке – минимум;

• если 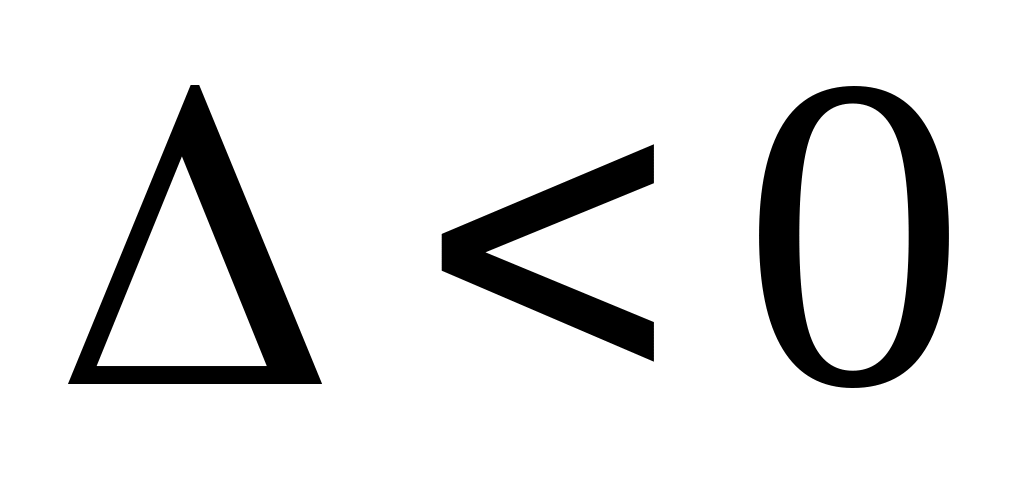, то экстремума нет;

• если 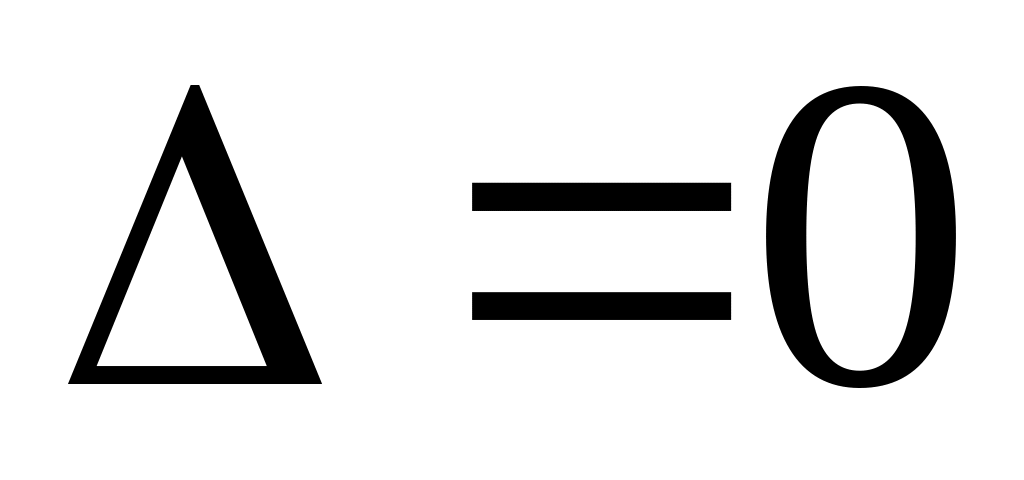, то вопрос об экстремуме остается открытым, а такая точка называется седловой.

_{Пример: исследовать на экстремум функцию} .

Решение: находим частные производные:

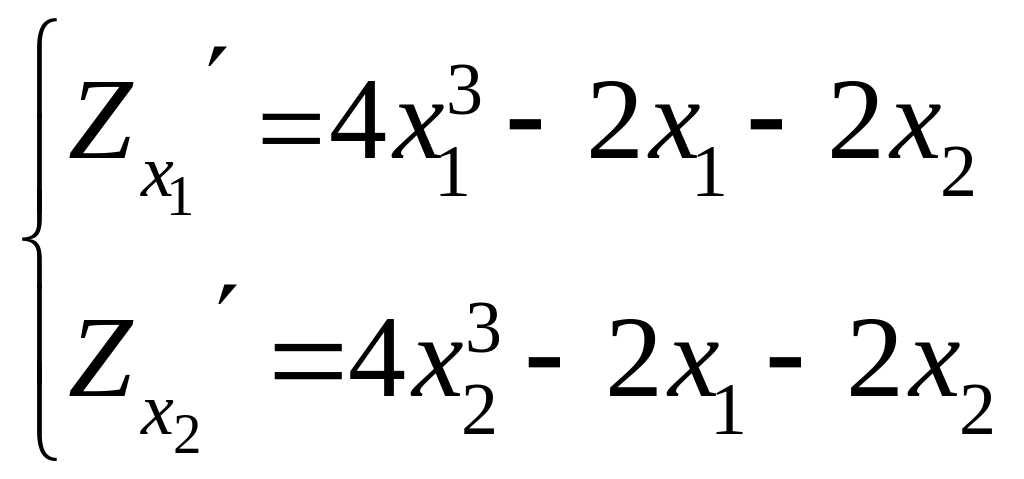
Приравниваем частные производные нулю:

Решаем систему уравнений.

Вычитая из первого уравнения второе, получим , поэтому и из первого уравнения найдем , откуда или .

Имеем три стационарные точки: ; ; .

Найдем вторые частные производные:

Вычисляем значения вторых частных производных в каждой стационарной точке, составляем определитель и применяем достаточные условия экстремума. В точке :

Вопрос об экстремуме остается открытым.

В точке , а также и в точке и :

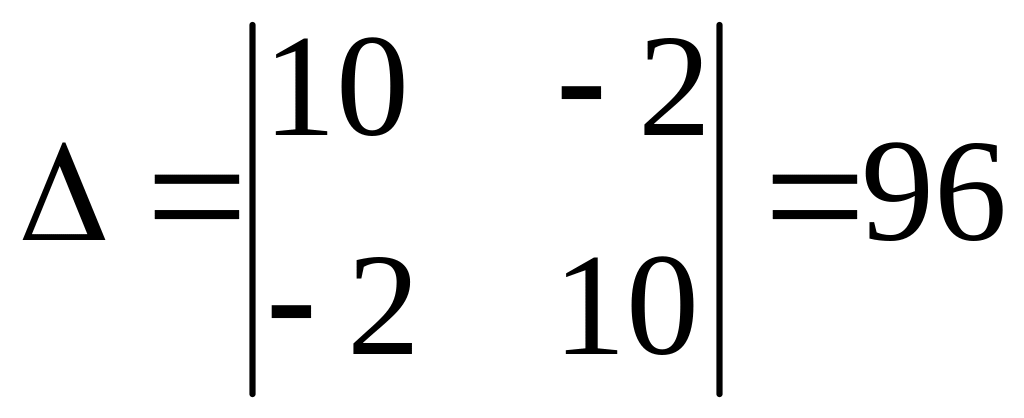
Функция в этих точках имеет минимум, так как и .