5. Скалярное, векторное, смешанное произведение векторов.

Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

 =   cos

Обозначение: (причем ).

Свойства скалярного произведения.

1.  =  ²;

2.  = 0, если  или = 0 или = 0.

3.  =  ;

4. ( + ) =  +  ;

5. (m ) = (m ) = m(  ); m=const

Если рассматривать векторы в декартовой прямоугольной системе координат, то  = x_a x_b + y_a y_b + z_a z_b;

Определение. Векторным произведением векторов и называется вектор , удовлетворяющий следующим условиям:

1) , где  - угол между векторами и ,

2) вектор ортогонален векторам и

3) , и образуют правую тройку векторов.

Обозначается: или .



Свойства векторного произведения векторов.

1) ;

2) , если  или = 0 или = 0;

3) (m ) = (m ) = m(  );

4) ( + ) =  +  ;

5) Если заданы векторы (x_a, y_a, z_a) и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами , то

 =

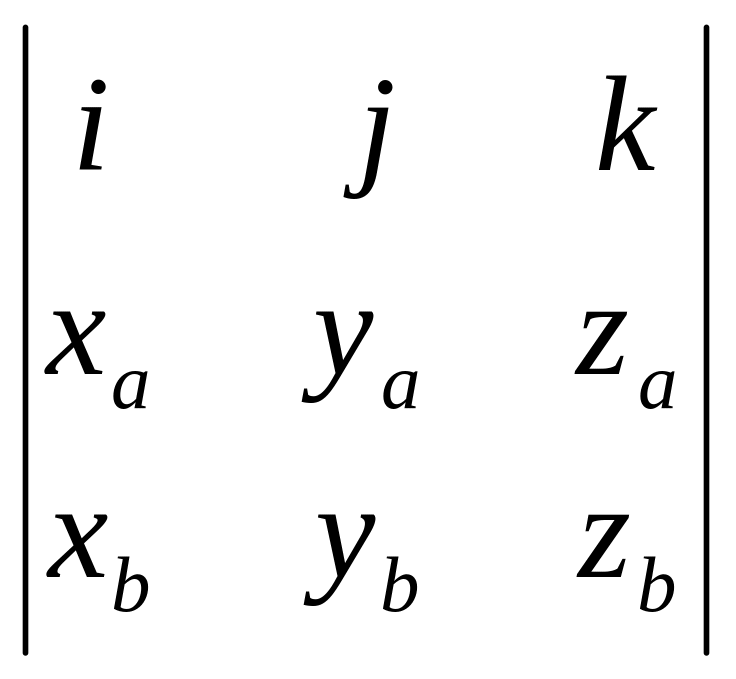
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

Определение. Смешанным произведением векторов , и называется число, равное скалярному произведению вектора на вектор, равный векторному произведению векторов и .

Обозначается или ( , , ).

Смешанное произведение по модулю равно объему параллелепипеда, построенного на векторах , и .

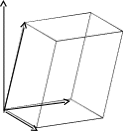
Свойства смешанного произведения.

1)Смешанное произведение равно нулю, если:

а) хоть один из векторов равен нулю;

б) два из векторов коллинеарны;

в) векторы компланарны.

2)

3)

4)

5) Объем треугольной пирамиды, образованной векторами , и , равен

6)Если , , то .

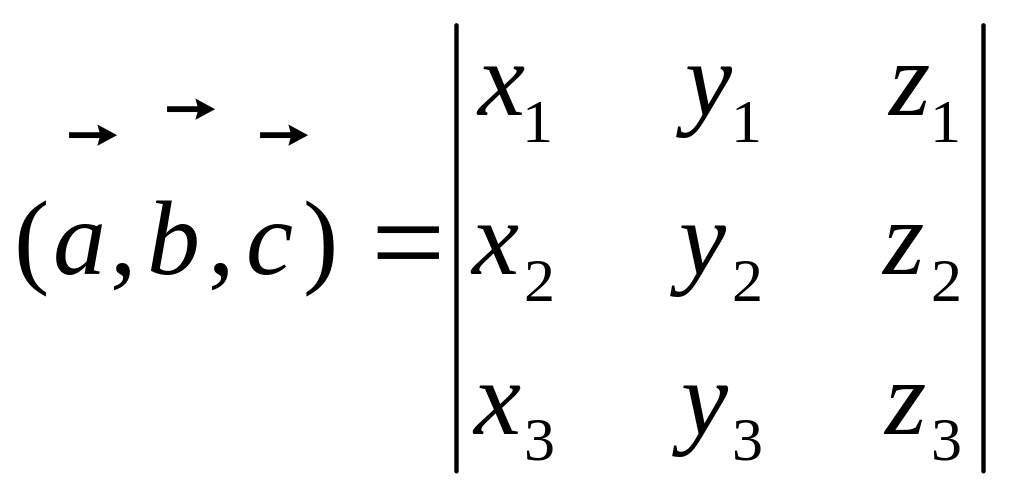6. Линейные операторы и матрицы. Собственные векторы линейных операторов.

Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.

Рассмотрим два линейных пространства: размерности n и размерности m.

Определение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор у пространства , то говорят, что задан оператор (преобразование, отображение) Ã(х), действующий из в , и записывают y=Ã(х).

Определение. Оператор (преобразование) называют линейным, если для любых векторов х и y пространства и любого числа ʎ выполняются соотношения:

1. Ã(x+y) = Ã(x) + Ã(y) -свойство адаптивности оператора;

2. Ã( ʎх) = ʎÃ(х) — свойство однородности оператора.

Вектор y=Ã(х) называется образом вектора х, а сам вектор х - прообразом вектора y.

Если пространства и совпадают, то оператор А отображает пространство в себя.

Выберем в пространстве базис . Запишем разложение произвольного вектора х по данному базису:

В силу линейности оператора Ã получаем

Поскольку ( l= 1,2,...,n) — также вектор из , то его можно разложить по базису .

Пусть (i = 1,2,…,n) (6.1)

Тогда

С другой стороны вектор y=Ã(х), имеющий в том же базисе координаты можно записать так:

Ввиду единственности разложения вектора по базису равны правые части равенства , откуда:

Определение. Матрица ( i,j =1,2,...,n) называется матрицей оператора Ã в базисе ,а ранг r матрицы А – рангом оператора Ã.

Таким образом, каждому линейному оператору соответствует матрица в данном базисе.

Справедливо и обратное: всякой матрице т-ого порядка соответствует линейный оператор т-мерного пространства.

Связь между вектором х и его образом y=Ã(х) можно выразить в матричной форме уравнением

Y=AX,

где А — матрица линейного оператора, , -матрицы-столбцы из координат векторов х и y.

Определение: Вектор ,называется собственным вектором линейного оператора Ā, если найдется такое число ʎ,что Ã(х)= ʎх (6.2)

Число ʎ называется собственным значением оператора Ã (матрицы А),соответствующим вектору х.

Из определения следует, что собственный вектор под действием линейного оператора А переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.

Равенство (6.2) можно записать в матричной форме:

АХ= ʎХ (6.3)

где Х — матрица-столбец из координат вектора х. Или в развернутом виде