22. Формула включений-исключений и ее применения к комбинаторике и теории чисел. Бином Ньютона.

Теорема 22.1. (формула включений-исключений) Если и конечные подмножества некоторого множества, – число элементов множества , – число элементов множества , число элементов множества , то

(22.1)

Установим общую формулу для определения числа элементов объединения конечного числа конечных множеств.

Теорема 22.2. Если конечные подмножества множества, то

.

или

(22.2)

где есть сумма чисел по всем возможным пересечениям ровно различных множеств из множеств .

Бином Ньютона (полиномиальная формула) - это формула, выражающая выражение в виде многочлена. Эта формула имеет вид:

,

- число сочетаний из элементов по k.

Широко известные формулы сокращенного умножения квадрата суммы и разности, куба суммы и разности являются частными случаями бинома Ньютона.

Когда степень бинома невысока, коэффициенты многочлена могут быть найдены не расчетом по формуле количества сочетаний, а с помощью треугольника Паскаля.

Формула бинома Ньютона может быть обобщена для произвольного числа слагаемых.

,

Применение формулы включений-исключений надо бы найти!!!!

23. Рекуррентные уравнения.

Определение. Если каждый последующий член числовой последовательности выражается через предыдущие , ,…, и при этом определены первые k ее членов, то говорят, что последовательность задана рекуррентно. Само число k назвается степенью, либо глубиной рекуррентности.

Простейшими примерами таких последовательностей являются хорошо знакомые со школы арифметическая и геометрическая прогрессии.

Если задано рекуррентное соотношение k-го порядка, то ему удовлетворяет бесконечно много последовательностей.

Дело в том, что первые k элементов последовательности можно задать совершенно произвольно - между ними нет никаких соотношений. Но если первые k элементов заданы, то все остальные элементы определяются совершенно однозначно - элемент выражается в силу рекуррентного соотношения через ; элемент - через и т.д.

Пользуясь рекуррентным соотношением и начальными членами, можно один за другим выписывать члены последовательности, причем рано или поздно получим любой ее член. Однако при этом придется выписать и все предыдущие члены - ведь не узнав их, мы не узнаем и последующих членов. Но во многих случаях нужно узнать только один определенный член последовательности, а остальные не нужны. В этих случаях удобнее иметь явную формулу для -го члена последовательности. И когда ставится задача нахождения формулы общего члена последовательности, заданной рекуррентным соотношением, употребляется термин рекуррентное уравнение. Явно заданная последовательность, удовлетворяющая рекуррентному уравнению, называется решением этого уравнения.

Для решения рекуррентных уравнений общих правил, вообще говоря, нет. Однако существует весьма часто встречающийся класс уравнений, решаемый единообразным методом. Это - рекуррентные уравнения вида

, (23.1)

где - некоторые числа. Такие уравнения называют линейными однородными рекуррентными уравнениями с постоянными коэффициентами.

Ограничимся подробным изучением линейных рекуррентных уравнений второго порядка, так как все существенные черты данной теории могут быть показаны для этого случая.

Определение. Рекуррентные уравнения вида

(23.2)

где - некоторые числа, называют линейными однородными рекуррентными уравнениями второго порядка с постоянными коэффициентами.

Пправило решения линейных рекуррентных соотношений второго порядка с постоянными коэффициентами.

Пусть дано рекуррентное соотношение (23.2):

Составим квадратное уравнение

, (23.3)

которое называется характеристическим для данного уравнения.

При решении квадратного уравнения могут получиться:

1. Два различных корня 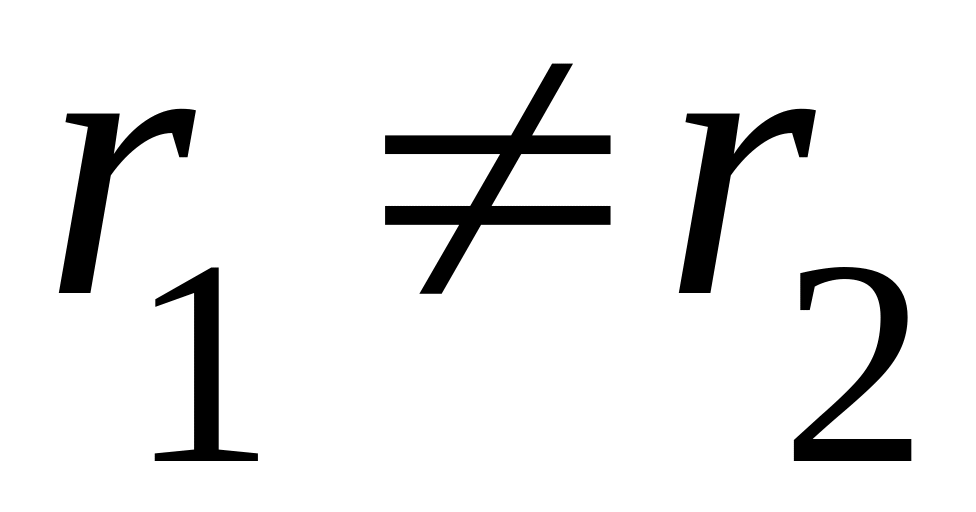, , тогда общее решение уравнения (23.2) имеет вид

(23.4)

Задача 23.1. Найдите решение рекуррентного уравнения

,

, при

Решение. Для него характеристическое уравнение имеет вид

Корнями этого квадратного уравнения являются числа

, .

Поэтому общее решение нашего рекуррентного уравнения имеет вид

Подставим , отсюда и , откуда и .

Следовательно, .

2. Два корня совпадают , , тогда общее решение уравнения (23.2) имеет вид

(23.5)

Задача 23.2. Найдите решение рекуррентного уравнения

, ,

, при

Решение. Для него характеристическое уравнение имеет вид

Корнем этого квадратного уравнения является число 2.

Итак, общее решение нашего рекуррентного соотношения имеет вид .

Подставим , отсюда и , откуда .

Следовательно, .

3. Оба корня характеристического уравнения комплексные числа: , , тогда общее решение уравнения (23.2) имеет вид

, (23.6)

где , , .

Задача 23.3. Найдите решение рекуррентного уравнения

, ,

, при

Решение. Для него характеристическое уравнение имеет вид

Корни этого квадратного уравнения: , .

Таким образом. , , .

Наконец, и , поэтому

Итак, общее решение нашего рекуррентного соотношения имеет вид .

Подставим , отсюда и , откуда .

Следовательно, .

Примеры разобраны для вас, их рассказывать на надо.