15. Производная, ее геометрический и физический смысл.

П усть функция определена в интервале (a;b) и непрерывна в точке , и пусть . В окрестности точки выбирается произвольная точка x. Тогда разность называется приращением аргумента в точке . А разность – приращением функции. На рисунке рассмотрим секущую, проведенную через точки M и N. Угол называется углом наклона секущей, а ее угловым коэффициентом.

Из прямоугольного треугольника MPN . Если точка N будет стремиться к M вдоль данной линии, то есть , то секущая MN в пределе перейдет в касательную l , а угол наклона секущей – , в угол наклона касательной – .

Определение:

Производной функции в точке называется предел отношения приращения этой функции к приращению аргумента, когда последний стремится к нулю, т.е .

Геометрический смысл производной.

Из рассуждений, приведенных выше видно, что производная функции при равна угловому коэффициенту касательной к графику данной функции в точке , т.е .

Физический смысл производной.

Если – закон прямолинейного движения точки, то – скорость этого движения в момент времени t.

Быстрота протекания физических, химических и других процессов выражается с помощью производной.

Сила и импульс по второму закону Ньютона связаны соотношением:

Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока:

В электростатическом поле, изменяющемся только по оси OX, напряженность и потенциал связаны соотношением:

16. Дифференциал, его геометрический и механический смысл.

Пусть функция , определенная в некотором промежутке имеет производную в точке x.

.

Тогда можно записать , где при

Следовательно:

, где – бесконечно малая высшего порядка по сравнению с .

Определение: Дифференциалом функции в точке называется главная часть ее приращения, линейная относительно приращения аргумента. или .

Вычислим: . Следовательно

Пример 16.1. Найти дифференциал данной функции:

a) ,

b)

Решение: Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:

a) ;

b)

.

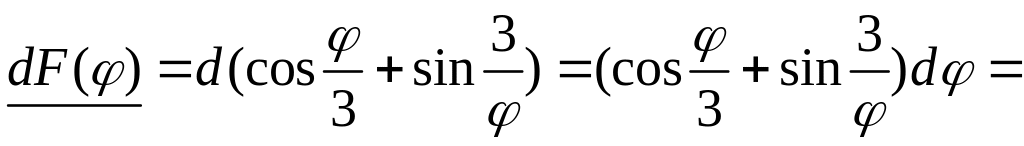
Геометрический смысл дифференциала.

Д ифференциал функции равен приращению ординаты касательной к графику функции в соответствующей точке, когда аргумент получает приращение .

Действительно на рисунке PN это приращение функции, а PT это приращение по касательной, или дифференциал.

Отметим, что может быть ,или – это зависит от направления выпуклости функции. тогда когда , т.е. функция равна постоянной.

Дифференциал обладает свойствами, аналогичными свойствам производной.

Кстати, механический смысл было бы неплохо дописать!

17. Теоремы о дифференцируемых функциях и их применение.

Определение. Функция называется дифференцируемой, если во всех точках данного множества имеет производную.

Определение. Пусть функция определена на некотором множестве , и . Назовём точку точкой максимума функции на множестве , если при всех выполняется неравенство , и точкой минимума, если при всех выполняется неравенство . Точка , являющаяся либо точкой максимума, либо точкой минимума, называется точкой экстремума.

Теорема 17.1. (Ферма)   Пусть функция имеет на множестве точку экстремума , причём множество содержит некоторую -окрестность точки . Тогда либо имеет в точке производную, равную 0, то есть , либо производная в точке не существует.

Доказательство.     Если производная в точке экстремума не существует, то утверждение теоремы верно. Предположим, что производная существует. Рассмотрим два случая.

1. Пусть функция имеет в точке максимум. Тогда при всех , поскольку . Если взять , то , и поэтому . При вычислении производной мы переходим к пределу при в этом разностном отношении. При этом знак нестрогого неравенства сохраняется, когда мы берём предел справа: 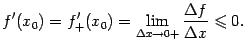Аналогично, при , , и поэтому . Отсюда, вычисляя предел слева, получаем: Итак, выполняются два неравенства: и , что возможно лишь при .

2. Пусть теперь функция имеет в точке минимум. Тогда при всех , поскольку . Если взять , то , и поэтому . Переходя к пределу при в разностном отношении, получаем:

Аналогично, при , , и поэтому . Вычисляя предел слева, получаем: Из неравенств и получаем, что .     

Замечание.   Заметим, что условие означает, что тангенс угла наклона касательной к графику , проведённой при , равен 0.

Рис.17.1. Поведение функции в окрестности точки экстремума

Геометрический смысл. Касательная, проведённая в точке экстремума, горизонтальна (если эта касательная существует).     

Пример 17.1.   Функция имеет на отрезке точку минимума . Производная функции существует при всех : . В точке минимума производная, действительно, оказывается равной 0: , так что утверждение теоремы Ферма выполнено.     

Рис. 17.2.График

Пример 17.2.   Функция имеет на отрезке точку минимума . Производная функции при не существует. (Производная существует при всех , она равна 1 при и при .) Итак, в точке минимума этой функции производная не существует, и утверждение теоремы Ферма снова выполнено.     

Рис. 17.3.График

Далее мы будем предполагать, что функция , заданная на отрезке , удовлетворяет следующим условиям: она непрерывна на отрезке и дифференцируема на интервале ; существование односторонних производных в точках и , вообще говоря, не предполагается. Непрерывность во всех внутренних точках отрезка, конечно, следует из предположенной дифференцируемости, а вот непрерывность в точках (непрерывность справа) и (непрерывность слева) из дифференцируемости в точках интервала не следует.

Теорема 17.2. (Ролля)   Пусть функция дифференцируема на интервале , непрерывна в точках и и принимает в этих точках значение 0: . Тогда найдётся хотя бы одна точка , в которой .

Доказательство.   Так как функция непрерывна на отрезке , то она принимает своё максимальное значение и минимальное значение в некоторых точках и этого отрезка. Рассмотрим два случая.

1. Если , то наибольшее и наименьшее значения функции совпадают, и, следовательно, функция постоянна на отрезке : . Значит, при всех , и в качестве в этом случае можно взять любую точку интервала .

2. Если же , то либо , либо отлично от 0 и, следовательно, либо точка , либо точка не совпадает с концами отрезка и , то есть лежит внутри интервала . Пусть, для определённости,   - внутренняя точка интервала. Тогда, по теореме Ферма, , поскольку по предположению доказываемой теоремы, имеет производную во всех точках интервала и, следовательно, в точке . Итак, в этом случае точку можно взять в качестве искомой точки : тогда .     

Замечание.   Теорему можно переформулировать так: между двумя корнями и дифференцируемой функции обязательно найдётся корень её производной (то есть точка , такая что ).

Геометрический смысл. Условие означает, что касательная, проведённая к графику при , расположена горизонтально.

Рис.17.4.

Теорема Ролля не утверждает, что корень  - единственный корень производной на интервале ; на этом интервале может находиться несколько корней производной.     

Теорема 17.3. (Лагранжа)   Пусть функция дифференцируема на интервале и непрерывна в точках и . Тогда найдётся такая точка , что

Доказательство. Сведём доказательство к применению теоремы Ролля. Для этого введём вспомогательную функцию , , то есть

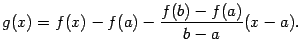
Заметим, что и . Так как функция дифференцируема при всех , то функция удовлетворяет всем свойствам, перечисленным в условии теоремы Ролля. Поэтому найдётся такая точка , что .

Заметим теперь, что

Значит, равенство можно переписать в виде

Замечание.   Формулу можно записать в виде

(17.1)

Если считать, что аргументу придано приращение , то функция получает приращение (При этом мы не считаем, что и стремятся к 0, то есть это конечные, а не бесконечно малые, приращения). При этих обозначениях формулу (17.1) мы можем записать в виде здесь участвуют конечные приращения аргумента и функции. Поэтому формулу (17.1) называют формулой конечных приращений.     

Геометрический смысл. Соединим конечные точки графика на отрезке хордой. Конечные приращения и  --это величины катетов треугольника, гипотенузой которого служит проведённая хорда.

Рис.17.5.Касательная в некоторой точке параллельна хорде

Теорема утверждает, что к графику дифференцируемой функции можно провести в некоторой точке касательную, которая будет параллельна хорде, то есть угол наклона касательной ( ) будет равен углу наклона хорды ( ).