- •Лекція розв’язання диференціальних рівнянь першого та другого порядку диференціювання
- •Диференціювання
- •Числове диференціювання
- •Символьне диференціювання
- •Диференціювання в частинних похідних
- •Застосування похідних при Розв’язаннІ економічних задач
- •Розрахунок продуктивності праці
- •Аналіз виробничих функцій
- •Еластичність
- •Функції для розв'язання звичайних диференціальних рівнянь.
Функції для розв'язання звичайних диференціальних рівнянь.
В MathCad є багато убудованих функцій для рішення диференціальних рівнянь. Всі вони, крім Odesolve, вимагають певної непростої форми запису рівнянь. Функція Odesolve дозволяє записувати рівняння в блоці рішення у звичному виді.
Звертання до функції Odesolve вимагає запису обчислювального блоку, у який входить три частини.
Ключове слово Given.
Диференціальне рівняння й початкові умови до нього або система диференціальних рівнянь й умови до неї.
Функція Odesolve(x, xk, n), де x – ім'я змінної, щодо якої вирішується рівняння; xk – кінець інтервалу інтегрування (початок інтервалу інтегрування зазначено в початкових умовах); n – необов'язковий внутрішній параметр, що визначає число кроків інтегрування, за які повинне бути знайдене рішення диференціального рівняння.
Чим більше n, з тим більшою точністю буде вирішене рівняння, тим більше буде час рішення.
Наявність інших математичних виражень в обчислювальному блоці між ключовими словами Given й Odesolve неприпустимо.
Вихідне рівняння можна записувати як з використанням оператора диференціювання, так і зі штрихом. Для уведення штриха використайте сполучення клавіш Ctrl+F7.
Функція Odesolve повертає рішення диференціального рівняння у вигляді функції, тому знайдене рішення можна інтегрувати й диференціювати.
Приклади використання функції Odesolve наведені нижче.
Исходное уравнение
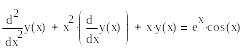
![]()
![]()
![]()
![]()
![]()
Дифференциальное уравнение
с начальными условиями
Розглянемо ще три функції, призначені для рішення диференціальних рівнянь й їхніх систем: rkfixed, Rkadapt, Bulstoer.
Звертання до цих трьох функцій виконується однаково:
rkfixed (y, x1, x2, m, D).
Аргументи функції перераховані нижче.
y – вектор початкових умов розмірності n (n – порядок диференціального рівняння або число рівнянь у системі, якщо вирішується система диференціальних рівнянь).
x1 й x2 – граничні точки інтервалу, на якому шукається рішення диференціального рівняння. Початкові умови, задані у векторі y,– це значення рішення в точці х1.
m – число точок, не враховуючи початкової, у яких шукається наближене рішення.
D – символьний вектор, у якому записані похідні невідомих функцій.
Функції rkfixed й Rkadapt реалізують метод Рунге-Кутта четвертого порядку.
Функції rkfixed шукає рішення з постійним кроком. Функція Rkadapt перевіряє, як швидко змінюється наближене рішення, і адаптує відповідно крок рішення. Це дозволяє підвищити точність і скоротити час рішення задачі. Функція Bulstoer використовує метод Булірша-Штера. Коли відомо, що рішення є гладкою функцією, то краще задіяти функцію Bulstoer. Знайдене функцією Bulstoer рішення є більш точним, ніж в інших функцій.
Для рішення диференціальних рівнянь або їх систем необхідно задати наступні величини:
початкові умови;
число точок, у яких треба знайти рішення;
саме диференціальне рівняння (або систему рівнянь), записане спеціальним чином.
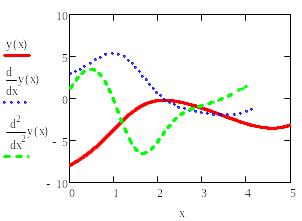
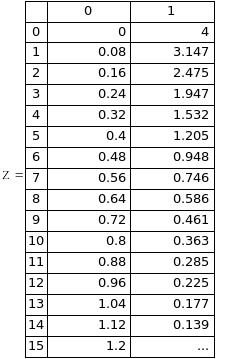
Знайдене рішення може бути представлене у вигляді таблиць або графіків.
ОДУ первого порядка
исходное уравнение
начальное приближение y(0)=4
первая производная в явном виде
решение с фиксированным шагом![]()
![]()
![]()
![]()
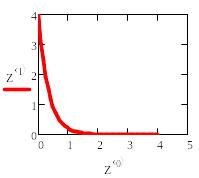
нелинейное уравнение
![]()
![]()
![]()
![]()
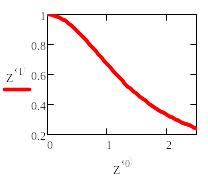
начальное приближение y(0)=1
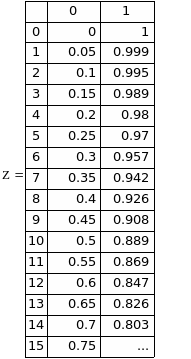
решение с переменным шагом
Виконати завдання.
Використовуючи функцію rkfixed або Rkadapt обчислити самостійно наступні рівняння:
![]() ,
, ![]()
![]()
![]()
![]()
![]() змінюйте початкові
умови.
змінюйте початкові
умови.
Обчислити самостійно за допомогою функції Odesolve:
![]()
![]()
![]()
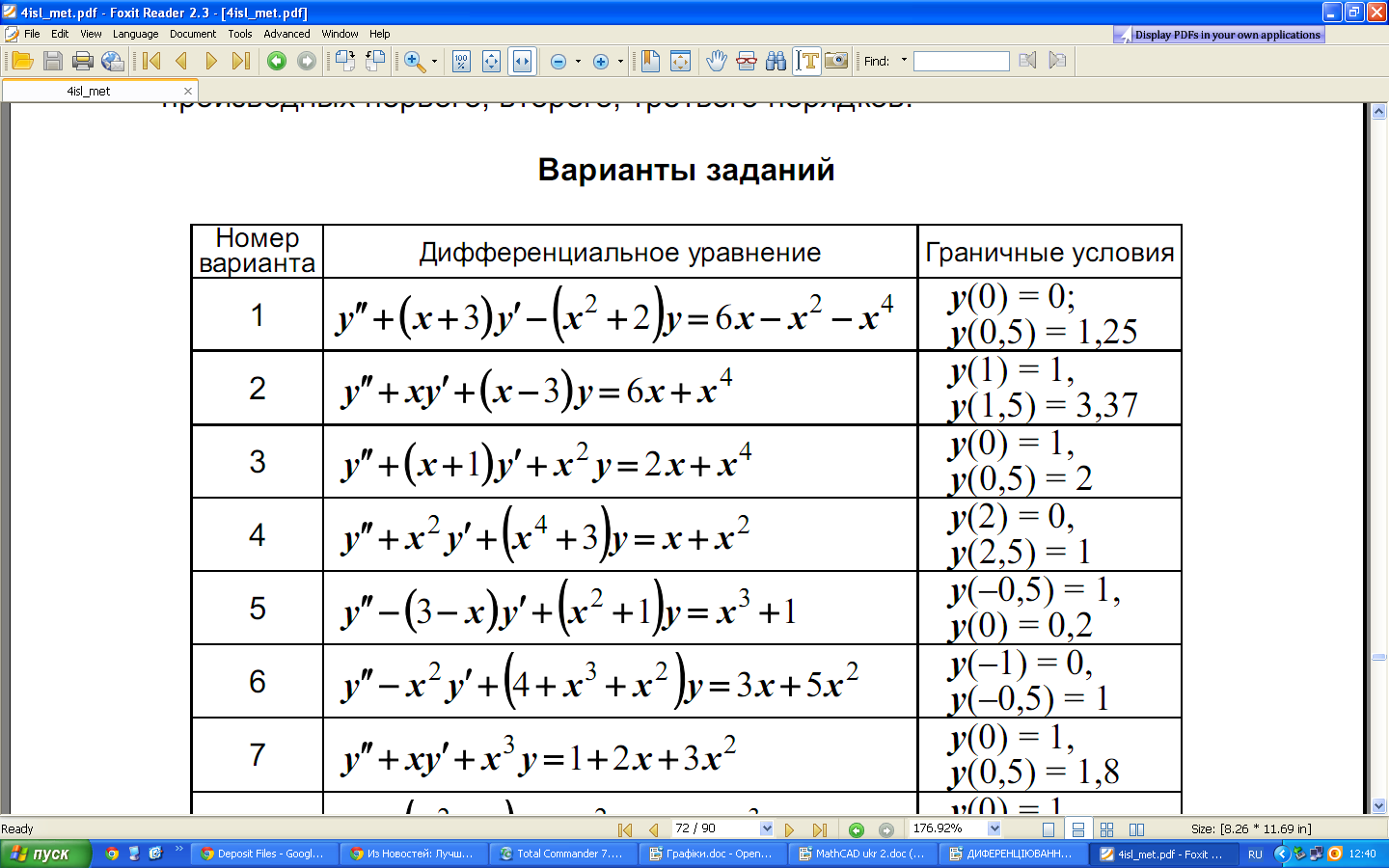
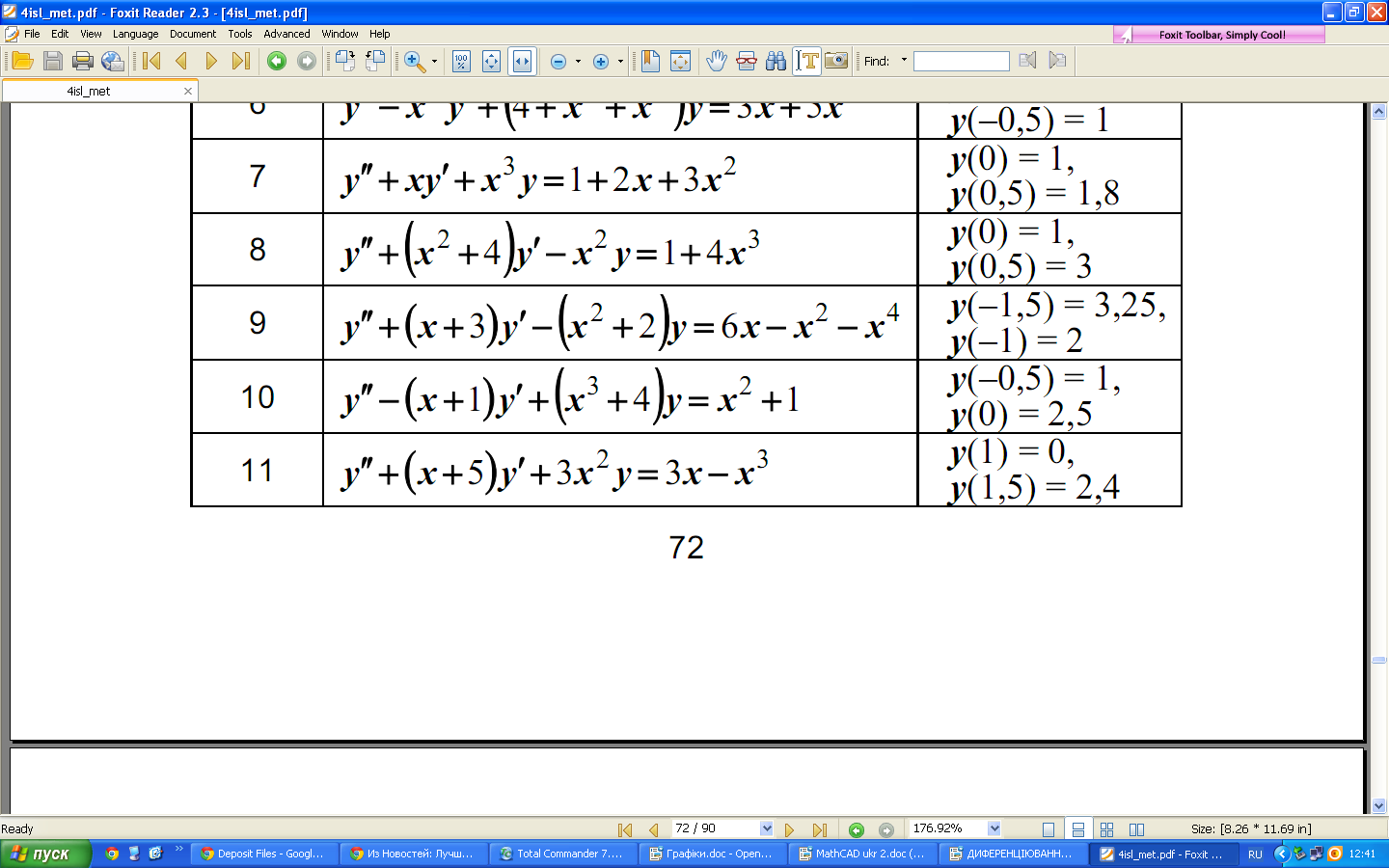
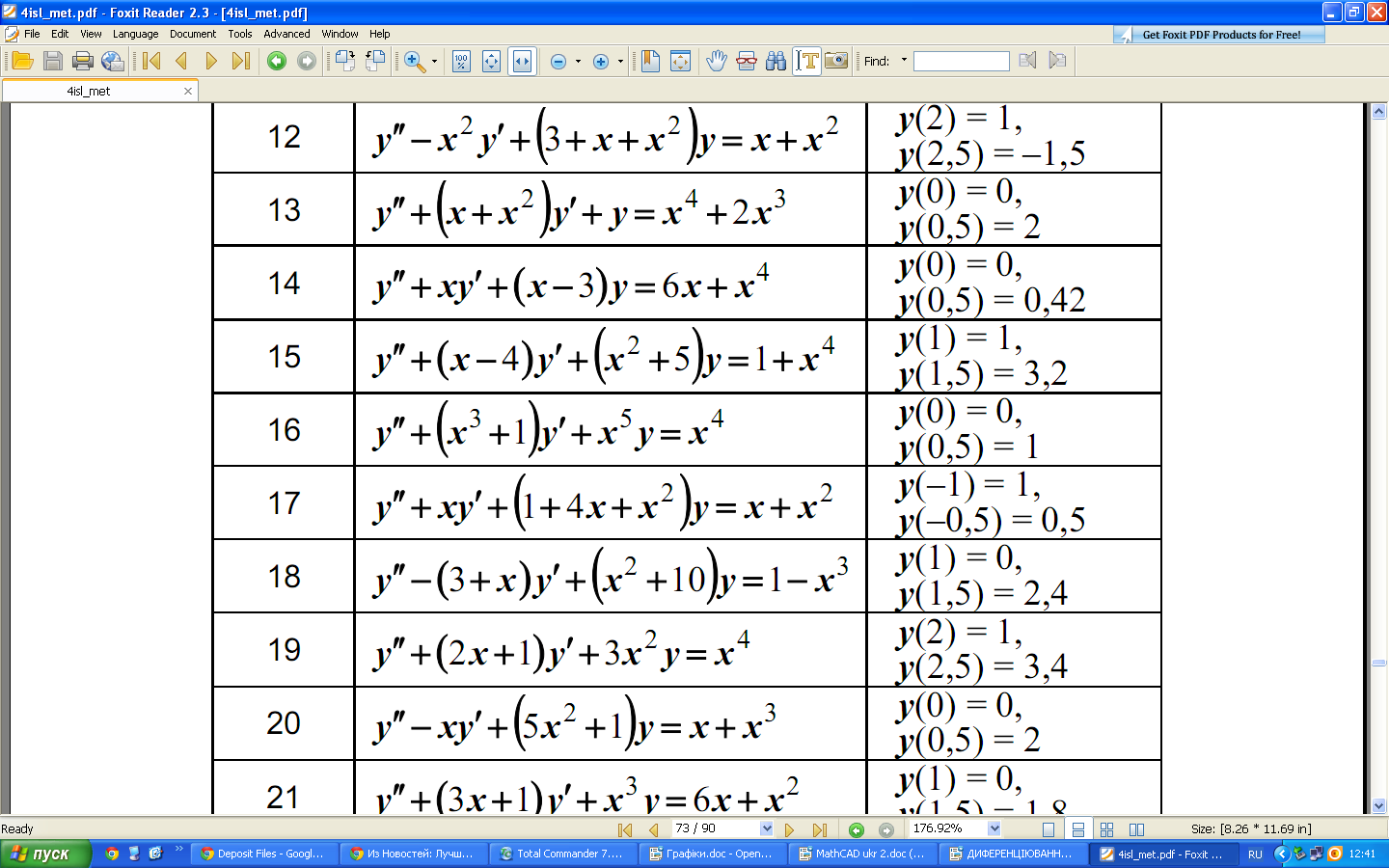
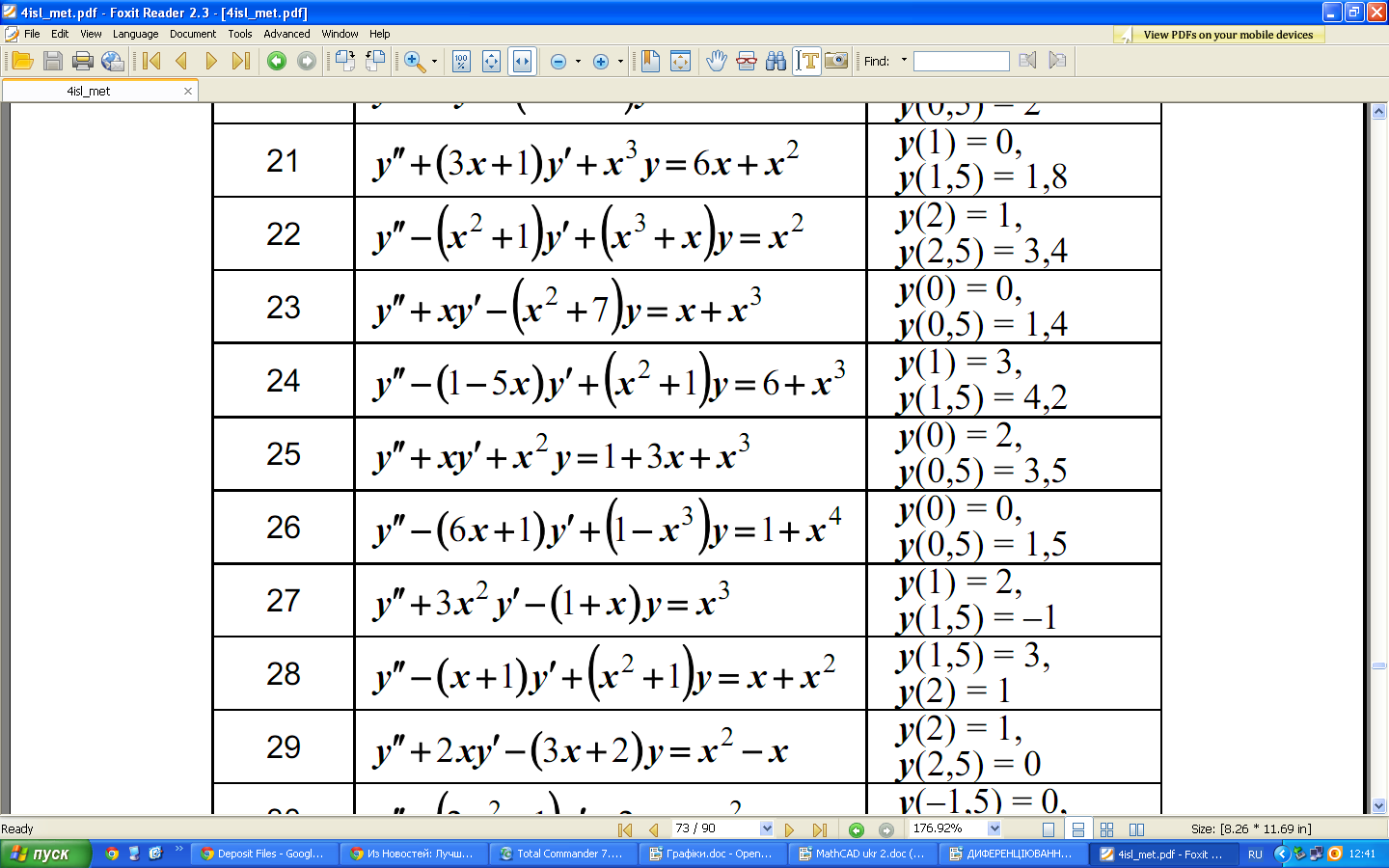
Індивідуальні завдання:
Завдання №1

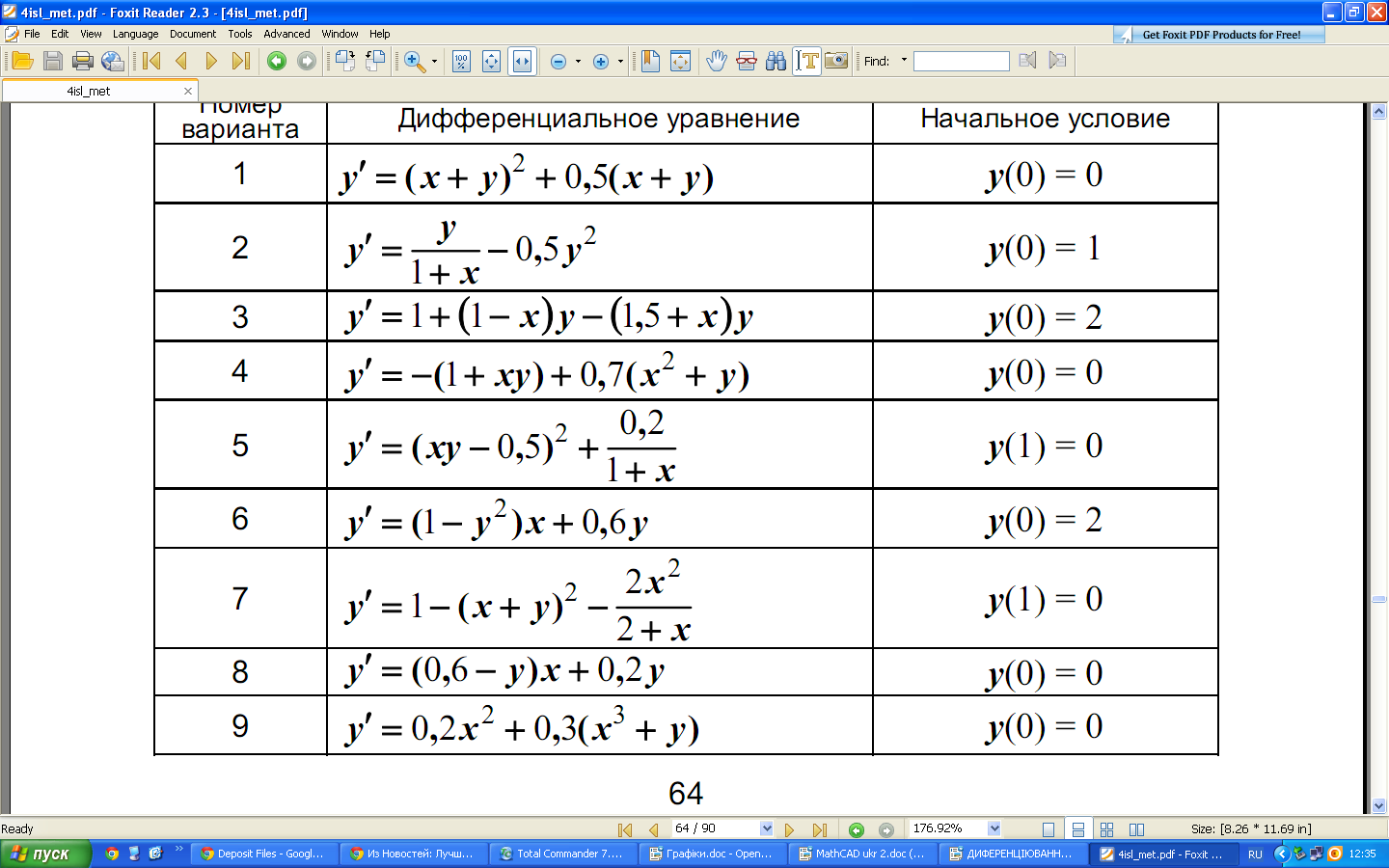
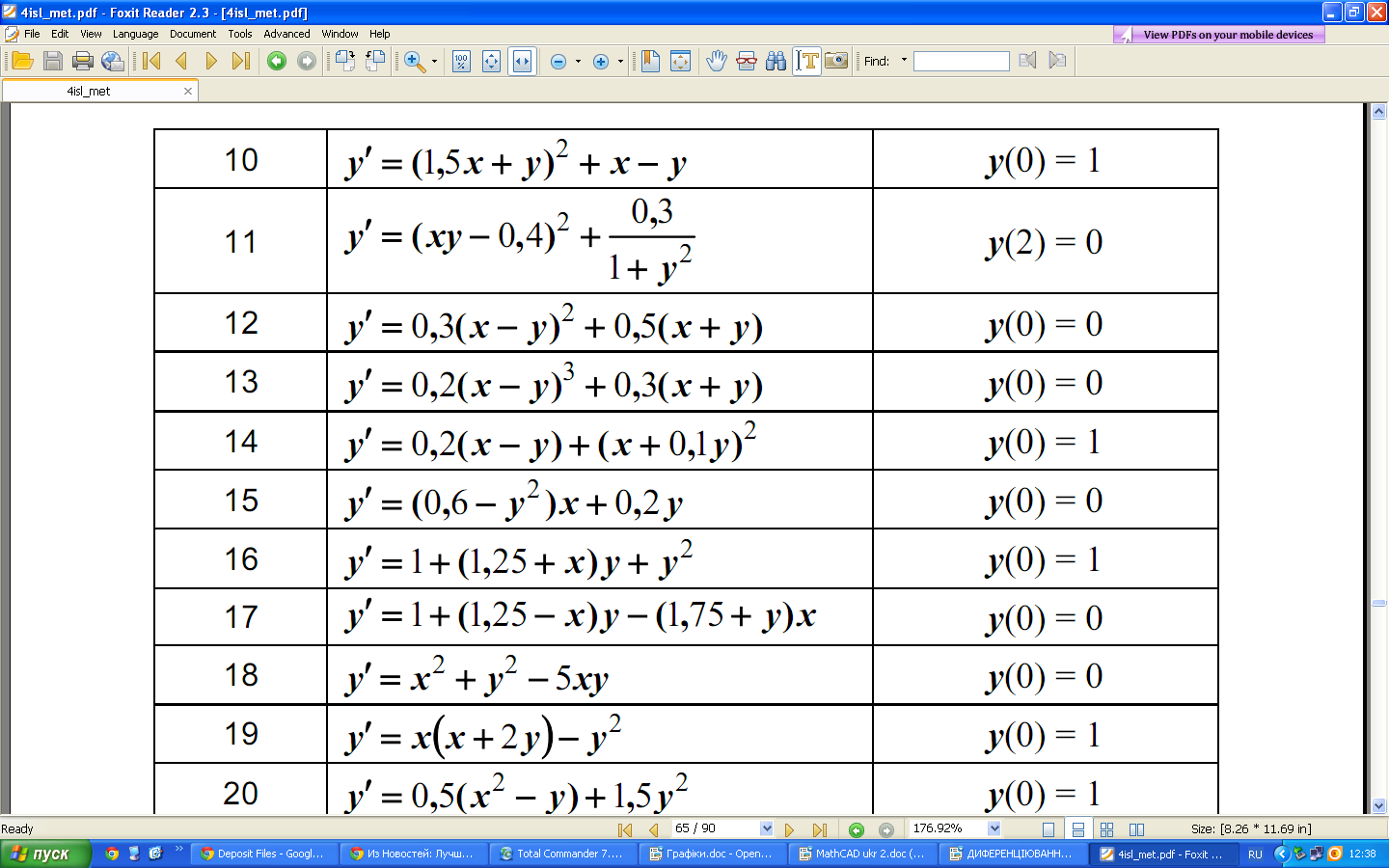

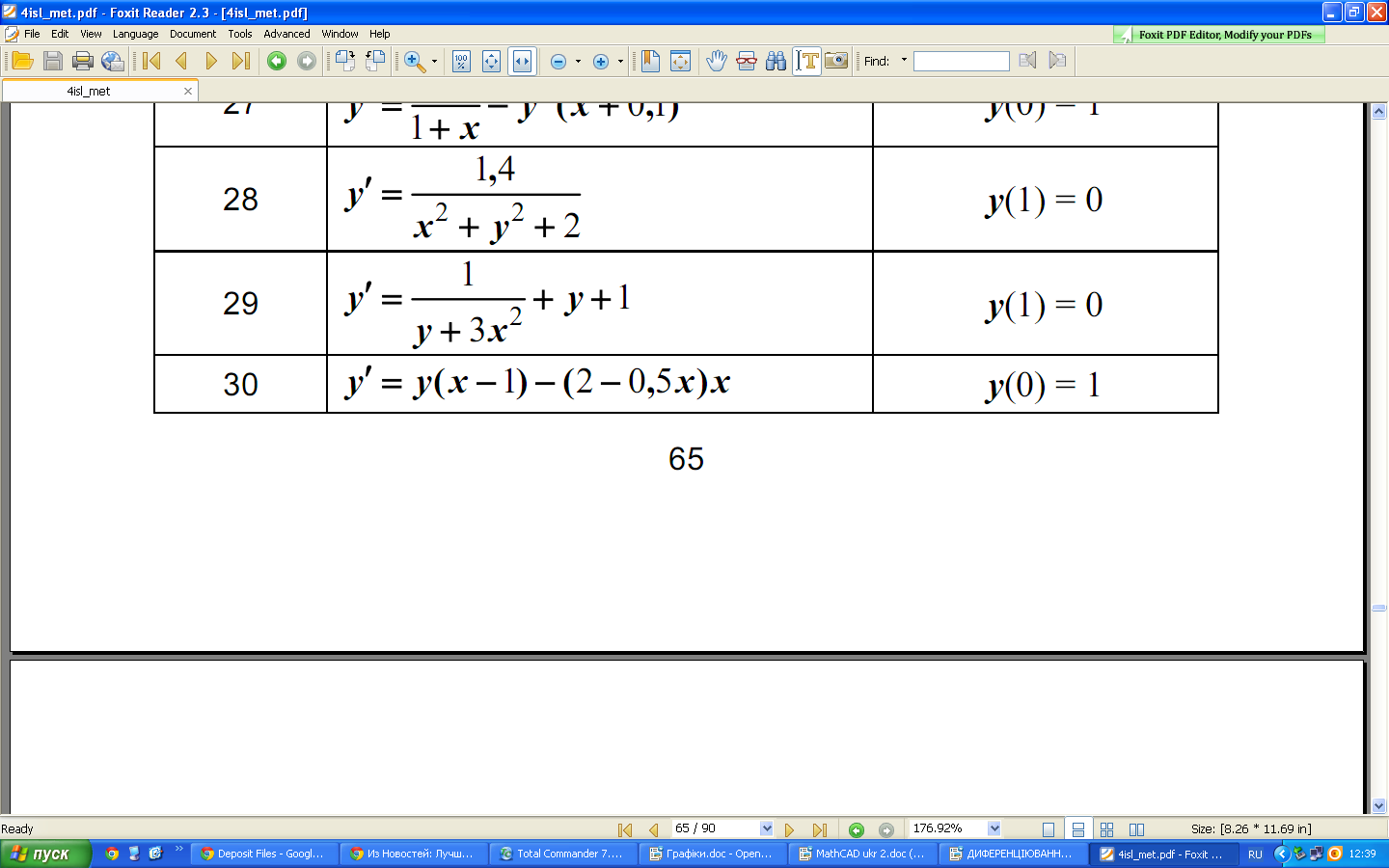
Завдання №2