34. Відкритий і оптичний резонатор.

Розглянемо резонатор, утворений паралельними плоскими нескінченно протяжними дзеркалами (рис.1), у якому відсутня робоча речовина й коефіцієнти відбиття від дзеркал рівні 100%.

У такому резонаторі можуть розглядатися в протилежних напрямках дві плоскі однорідні хвилі від однієї відбиваючої поверхні, що до іншої уздовж осі резонатора назустріч одна одної. При цьому утворюються стоячі хвилі, називані поздовжніми або аксіальними модами.

Об'ємним резонатором є прямокутний паралелепіпед з розмірами ребер L1, L2 і L3 і довжини хвиль власних типів коливань λ_mnq.

Щоб розрядити спектр власних частот, у оптичному діапазоні замість об'ємних резонаторів застосовують відкриті резонатори. Відкритим резонатором називають об'ємний резонатор відображаючи стінки якого не замкнуті.

34. Добротність резонатора.

Якщо враховувати всі види втрат в оптичному резонаторі, то в добротність резонатора прийме вид

, где – коэффициент потерь (для потерь на излучение ) або _ =_диф +_зер +_дис – сумарні втрати (дифракційні, у матеріалі дзеркал, диссипативные).

Знаючи добротність можна визначити ширину резонансного контуру

Добротність оптичного резонатора як добротність будь-якої коливальної системи, тобто

.

Окрім необхідних втрат на випромінювання в реальних резонаторах існують додаткові втрати.

34. Плоский резонатор.

Властивості плоского резонатора.

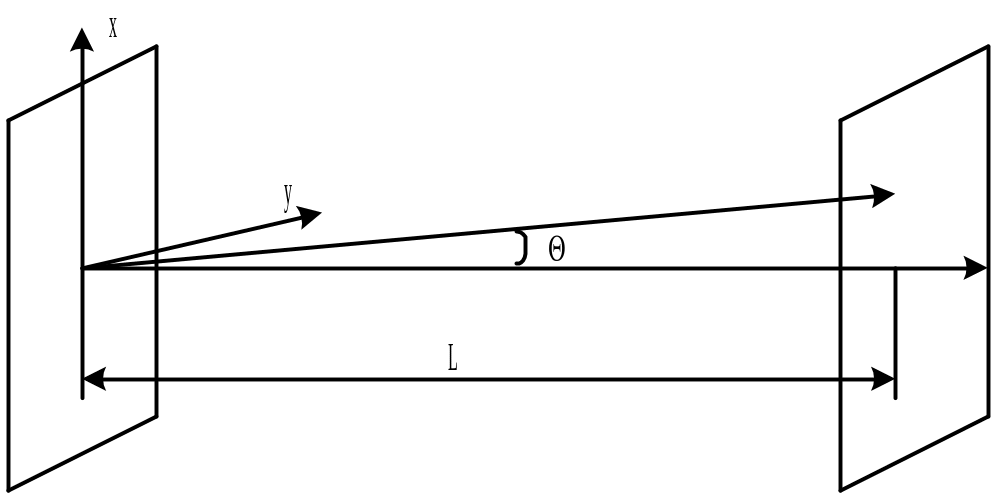
Це відкритий резонатор, у якому дзеркала мають кінцеві розміри й прямокутну форму.

а) б)

Рис. 3.3

У цьому випадку частота коливань

,

де m, n і q – цілі числа, що визначають кількість напівхвиль, що укладаються відповідно по осях x, y і z в об'ємному резонаторі; a, b – поперечні розміри резонатора; L – довжина резонатора.

Так як в оптичному резонаторі qm і qn, то одержимо:

.

Якщо поперечні розміри резонатора рівні, тобто а=b, тоді відстань між двома модами з однаковими значеннями m і n і (m=n) і значеннями, що відрізняються на одиницю, q дорівнює:

.

Різниця частот двох мод з однаковими значеннями q і значеннями, що розрізняються на одиницю, m і n називають межмодовым відстанню для двох сусідніх поперечних мод.

Для двох мод, що розрізняються значеннями m на одиницю, одержимо значення різниці частот

.

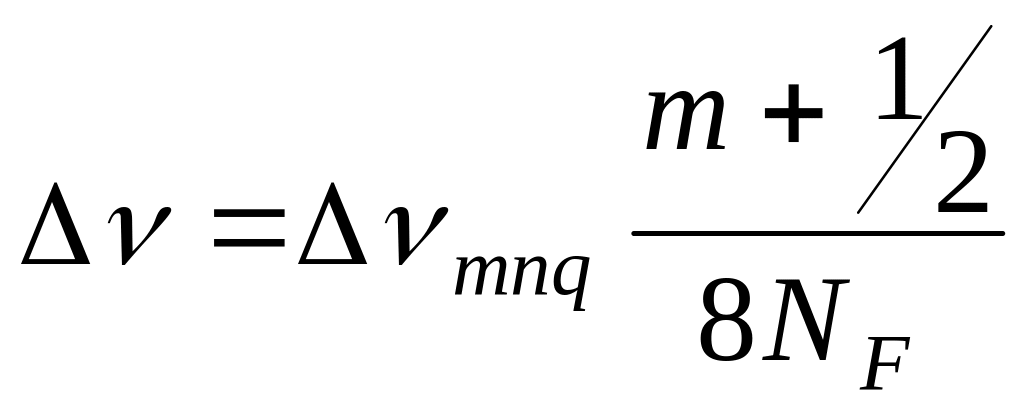Тут N_F = a²/L  = _m+1,_nq–_mq – безрозмірне число, називане числом Френеля.

Для реальних оптичних резонаторів звичайно N_F1, частотна відстань між поперечними модами менше, ніж між поздовжніми.

При кінцевих розмірах дзеркал кут θ не може приймати будь-яке значення. Різним поперечним модам відповідають дискретні значення θ.

34. Витрати на випромінювання. Втрати в активній речовині.

Втрати в активній речовині. Обумовлені поглинанням і розсіюванням енергії на різних дефектах в активному середовищі, що заповнює резонатор.

Постійна часу загасання моди резонатора:

яка називається також часом життя фотона. Цю величину використовують для характеристики втрат в резонаторі.

Для виведення випромінювання назовні одне з дзеркал резонатора повинно бути часткове проникним (напівпрозорим). Це втрати резонатора, звані втратами на випромінювання.

Добротність резонатора, яка визначається втратами на випромінювання: