Нижегородский государственный технический университет им Р.Е Алексеева

Курсовая работа по информатике

«Численное моделирование и анализ переходных процессов в электрической цепи»

Вариант №13

Выполнила: Мечетина С. В.

группа 11-Э-4

Проверила: Бажанов А.В.

г. Нижний Новгород

2012г

Содержание

Постановка задачи 3

Теоретическая часть 5

Практическая часть 13

2.Численная реализация решения систем дифференциальных уравнений (2) и (3) 13

2.1. Реализация решения в пакете MathCAD методом Эйлера (3 модификация). 13

1.2. Реализация решения в пакете MathCAD методом Рунге-Кутта. 16

1.3. Реализация решения на языке программирования высокого уровня (C++) методом Эйлера (3 модификация). 20

3. Решение задачи аппроксимации зависимости I(t) на интервале 25

3.1. Реализация решения в пакете Excel. 25

3.2. Реализация решения в пакете MathCAD, используя алгоритм метода наименьших квадратов. 27

4. Численное интегрирование 31

4.1. Реализация решения на языке программирования высокого уровня C++ методом трапеции. 31

4.2. Реализация решения в пакете MathCAD 33

Список литературы 39

Приложения 40

Постановка задачи

Дана схема электрической цепи, содержащая источник переменного тока, катушку индуктивности, конденсатор, набор резисторов и ключ (рис. 1).

Рис. 1.

Параметры элементов цепи:

– гармонический источник тока; = 15 В – амплитуда колебаний; – циклическая частота; f, Гц – линейная частота; – фаза; t – текущее время; = 30 Ом, = 25 Ом, = 50 Ом, = 1,88 Ом, = 15 Ом, = 50 Ом – резисторы; L = 5,57 мГн – катушка индуктивности; C = 20 мкФ – конденсатор. Параметры f, для данного варианта принимают следующие значения: f = 100 Гц;. = π/5

В начальный момент времени ключ находится в положении 1. При этом цепь разомкнута, напряжение на конденсаторе и ток в катушке равны нулю (U = 0, I = 0). Происходит первое переключение ключа (ключ мгновенно переводится в положение 2). При этом происходит заряд конденсатора, меняются значения U и I.

В момент времени ключ мгновенно переключается в положение 1. Конденсатор разряжается, вновь меняются значения U и I. Анализ схемы заканчивается в момент .

Вывод системы дифференциальных уравнений.

В соответствии с рисунком запишем выражения для I и II законов Кирхгофа для положения ключа 1:

(1)

Систему (1) можно преобразовать, исключив токи I₁ и I₂. Тогда для величин I и U получим систему дифференциальных уравнений первого порядка:

(2)

Аналогично может быть получена система дифференциальных уравнений для величин I и U при положении ключа 2. В этом случае имеем:

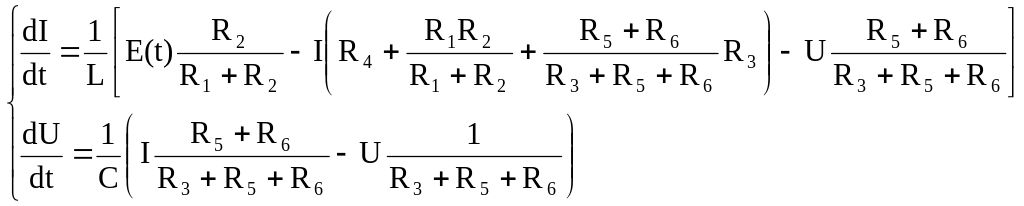(3)

В интервале решается система (3) с начальными условиями: ; В интервале решается система (2). В качестве начальных условий для системы (2) , следует использовать соответствующие значения, полученные в результате решения системы (3).

Теоретическая часть

1. Аппроксимация – это задача, в результате решения которой находят некоторую аппроксимирующую функцию f(х), такую, чтобы отклонения ее от заданной табличной функции было наименьшим. Чаще всего функцию f(х) представляют в виде полинома по степеням х. Общий вид полинома n-ой степени: f(x)=a₀+a₁x+a₂x²+…+a_nxⁿ.

2. Метод наименьших квадратов. Пусть общее количество точек равно m. Неизвестные коэффициенты а₀,а₁,…a_n, n находим из условия минимизации суммы квадратов отклонений искомой функции от исходных точек. Опуская промежуточные преобразования получим систему уравнений: Z⋅A=B, где Z – квадратная матрица размерностью (n+1)x(n+1), составленная из известных координат точек, А – вектор неизвестных коэффициентов; В – вектор-столбец свободных членов (i=1,m).

; ; (1)

3. Интерполяция – является частным случаем аппроксимации. Это задача о нахождении такой аналитической функции f(х), которая принимает в точках (узлах) x_i заданные значения y_i