
- •1.2. Основные понятия теории множеств и 1.3. Основные структуры.
- •1.4. Перестановки.
- •1.5. Размещения.
- •1.6. Сочетания.
- •2. Теория вероятности.
- •2.1. Классическое определение вероятности.
- •2.2. Теоремы сложения и умножения вероятностей.
- •2.3. Дискретные случайные величины.
- •2.4. Нормальный закон распределения вероятностей.
- •2.5. Основные понятия теории вероятности.
- •2.6. Аксиомы теории вероятности.
- •3.1. Дифференциальное исчисление функции одной переменной
- •3.2. Разрыв функции.
- •3.3. Функция. График.
- •3.4. Понятие дифференциального уравнения
- •4.1. Языки программирования высокого уровня
- •4.2. Задачи на циклы с параметром.
- •4.3. Алгоритмы
- •4.4. Работа с заданными массивами.
- •4.5. Блок – схемы. Ветвление.
- •4.6. Блок – схемы. Циклы с проверкой условия.
- •Текстовые редакторы. Таблицы
- •Электронные таблицы. Встроенные функции.
- •5.3. Компьютерная графика
- •5.4. Служебные программы.
- •5.7. Основные компоненты операционных систем.
- •5.8. Обзор программного обеспечения.
- •Двоичная система счисления.
- •Представление чисел в различных системах счисления
- •6.2 Количество информации.
- •Интернет
- •Конфигурация и топология цепей
- •Структура сообщений
- •Адресация в Интернет
- •Способы подключения к Интернету
- •Защита информации. Шифрование.
- •4. Ошибки обслуживающего персонала или пользователей.
- •5. Неправильное хранение информации.
- •Кодирование информации
4.2. Задачи на циклы с параметром.
Операторы цикла с пред- и постусловием, несмотря на то что обладают значительной гибкостью, не слишком удобны для организации «строгих» циклов, которые должны быть выполнены заданное число раз. Оператор цикла с параметром используется именно в таких случаях.
for <параметр_цикла>:=<начальное_знач.> to <конечное_знач.> do
<оператор>;
for <параметр_цикла>:=<конечное_знач.> downto <начальное_знач.> do
<оператор>;
Оператор, представляющий собой тело цикла, может быть простым или составным. Параметр цикла, а также диапазон его изменения могут быть только целочисленного или перечислимого типа. Параметр описывается совместно с другими переменными. Шаг цикла for всегда постоянный и равен интервалу между двумя ближайшими значениями типа параметра цикла. Например:
var { Описание параметров цикла. }
i: integer; c:char; b: boolean; begin {Вывод на печать целых чисел от 1 до 10.}
for i:=l to 10 do writeln(i);{ Шаг цикла равен 1. }
{ Вывод на печать чисел от 10 до -10, }
for i:=10 downto -10 do { Шаг цикла равен -1. }
writeln(i);
{ Вывод на печать латинских символов от а до r. }
{ Параметр цикла изменяется от а до г в алфавитном порядке. }
for c:='a' to 'r' do writeln(c); end.
Выполнение цикла начинается с присвоения параметру стартового значения. Затем следует проверка, не превосходит ли параметр конечное значение. Если результат проверки утвердительный, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. В противном случае выполняется тело цикла, и параметр меняет свое значение на следующее согласно заголовку цикла. Далее снова производится проверка значения параметра цикла, и алгоритм повторяется. В блок-схемах такие циклы изображаются так, как показано на рис. 3.2.
Здесь i- переменная цикла, in- начальное значение переменной цикла, ik- конечное значение переменной цикла. Блок, в котором указаны все эти значения, называется блоком модификации. Шаг изменения переменной цикла равен единице. Алгоритм, изображенный на
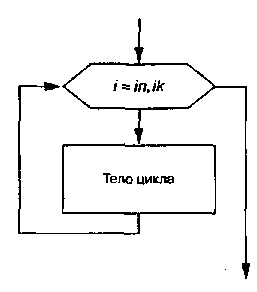
рис. работает следующим образом: переменной цикла присваивается начальное значение, затем значение переменной в цикле с параметром цикла увеличивается на единицу, и цикл повторяется. Так продолжается до тех пор, пока переменная цикла не превысит свое конечное значение, после чего цикл заканчивается. Если шаг изменения равен-1, то в блоке модификации мы напишем: i:=in,ik,-1.
ПРИМЕР 3.10. Вычислить факториал числа N (N!=l*2*3* ...*N). Блок-схема приведена на рис. 3.3.
Входные данные: N - целое число, факториал которого необходимо вычислить.
Выходные данные: factorial - значение факториала числа N. Промежуточные данные: i - параметр цикла.
Вводится число N. Переменной factorial присваивается начальное значение. Затем организуется цикл, причем в блок-схеме для этого используется блок модификации. Здесь параметру цикла i присваивается начальное значение 1, и цикл повторяется до N с шагом 1. Когда параметр r становится больше N, цикл заканчивается, и на печать выводится значение переменой factorial, которая была вычислена в теле цикла.
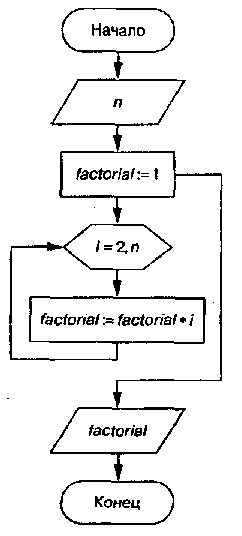
Рис. 3.3 т Алгоритм вычисления факториала
Теперь рассмотрим текст программы вычисления факториала на языке Турбо Паскаль.
var
factorial, n, i: integer;
begin
write('n=');
readln(n);
factorial:=1,- { Стартовое значение. }
for i:=2 to n do
factorial:=factorial*i;
writeln(factorial);
end.
