Уравнение движения ротора и формы его записи

Справедливо для всех типов машин. Все величины в относительных единицах(о.е.)

;

В стационарном режиме: ;

– постоянная инерции ;

для СГ: до десятков секунд.

– ускорение.

– демпферная мощность; коэффициент трения мех. действия эл. магнитного

– угловая скорость абсолютная , либо относительная.

– электромагнитная мощность.

В простейшем случае для синхронной машины:

1. Угол.

всегда будем иметь дело ;

1рад=57.3⁰

2. Время.

∙ω₀=1 [рад] ; ;

; 3.14 рад=1 секунда.

3. Скорость.

от неподвижной оси (абсолютная скорость)

– относительная скорость по отношению к синхронно вращающейся оси.

В дальнейшем будем работать с относительной скоростью.

Может быть представлена и в относительных и в именованных единицах.

при ,

4. Мощность.

При выражении угла в градусах:

,

_,

– СМ, АМ (всё в о.е.).

СГ упрощённая характеристика ЭМ:

В этом случае: ,

Без учёта демпферного момента: ,

П: →град; →с

,

_,

_,

.

С.К. в о.е.

,

Асинхронные машины:

,

,

,

– упрощённая.

_,

; .

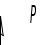
Рисунок.1.13 Характеристика электромагнитных моментов асинхронных машин.

Математическая формулировка задачи исследования статической устойчивости.

Исследование статистической устойчивости методом малых колебаний.

Таблица 1.2 – Исследование устойчивости.

, где -уравнение; -переменная; А, В, С- нелинейные функции, постоянные переменные, функционалы и т.д. -возмущение, момент силы; При , , - уравнение стационарного режима при малых отклонениях , -отклонение. Линеаризация-замена нелинейных функций в точке исходного режима линейными соотношениями. -линеаризированная система

. Рисунок 1.14 Угловая характеристика. Рисунок 1.15 Линеаризация угловой характеристики. , , , , .

Лепунов доказал, что характер процесса при линеаризации подобен процессам в реальной нелинейной системе при малых возмущениях.

Теорема Лепунова

1. Если все корни характеристического уравнения имеют отрицат- ельную вещественную часть, то система статически устойчива.

2. Если имеется хотя бы одна положительная вещественная часть, то система статически не устойчива.

;

Решим уравнение (*):

приведённое уравнение.

;

Пример. =0 Пример . =0.

С₁>0, ,

.

.

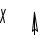
Рисунок 1.16 Колебательная Рисунок 1.17 Апериодическая характеристика характеристика.

1. (+); С₁>0,

,

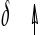
Рисунок 1.18 Колебательная устойчивость.

2.(+) ; С₁>0.

(-); (-).

Рисунок 1.19 Апериодическая устойчивость.

Характер протекания п.п. в зависимости от видов корней характеристического уравнения.

.

Для регулируемых систем:

;

Существуют алгебраические и частотные методы, способствующие нахождению отд. функций.

Метод Гурвица.

_.

не будет апериодической неустойчивости.

,

,

П.

.

Влияние реактивного сопротивления системы и насыщения генератора на статическую устойчивость.

Рисунок 1.20 Исходная схема.

Рисунок 1.21 Схема замещения.

.

Рисунок 1.22 Предел передоваевой мощности.

.

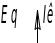
В дальнейшем насыщение учитывать не будем.

Рисунок 1.23 Характеристики режимов.

Явнополюсность машины. Угловая характеристика явнополюсной машины.

;

.

внутренняя ЭДС

Рисунок 1.24 Векторная диограмма генератора. ,

Обычно амплитуда второй гармоники не превышает 15% от амплитуды основной.

Р_р- реакционная мощность.

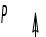
Рисунок 1.25 Угловая характеристика мощности синхронной машины.

. Проведём анализ преобразовав следующую схему в четырёхполюсник.

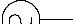Рисунок 1.26 Схема замещения при сложной связи.

З аменим нашу схему Т-образным 4^хполосником:

.

.

Применим принцип наложения, справедливый для линейных схем.

Рисунок 1.27 Т-образная схема замкщения.

Рисунок 1.28 Частичный режим 1.

.

Рисунок 1.29 Частичный режим 2.

;

Рисунок 1.30 Расположение векторов.

Принимаем ; ;

Переходим к тригонометрической форме записи:

,

,

,

Угловая характеристика мощности

,

,

.

Анализ устойчивости осуществляется по характеристике генератора

Пример.

Рисунок 1.31 Расчётная схема.

,

.

Рисунок 1.32 Угловая характеристика мощности.

Для схемы из двух генераторов соизмеримой мощности.

,

.

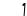
Рисунок 1.33 Расчётная схема.

Для систем , состоящих из большого числа генераторов.

Рисунок 1.34 Расчетная схема.

,

.

Влияние параметров системы на угловые характеристики мощности.

Пример.

Рисунок 1.35 Влияние индуктивного шунта.

Без шунта

; ; .

Рисунок 1.36 Угловая характеристика мощности.

С шунтом

.

,

.

с шунтом и регулированием E

Пример.

Рисунок 1.37Влияние ёмкостного шунта.

Без С:

.

С-С:

.

Рисунок 1.36 Угловая характеристика мощности.

Учет нагрузки и действительный предел мощности.

Рисунок 1.39 Расчётная схема.

Рисунок 1.40 Векторная диаграмма при изменении угла.

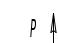
Рисунок 1.41 Действительный предел мощности.

Учет постоянного сопротивления z_н=const

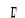
Рисунок 1.42 Расчётная схема.

.

Статическая устойчивость при регулировании возбуждения.

Рисунок 1.43 Схема замещения.

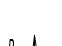
Рисунок 1.44 Угловая характеристика мощности.

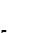
Рисунок 1.45Векторная диограма при учёте возбуждения.

.

Каждой новой области соответствует новая угловая характеристика.

вплоть до .

-внешняя характеристика генератора с регулированием.

,

-внутренний предел мощности (для генераторов с несовершенными системами регулирования).

- зона с искусственной устойчивостью.