1.5 Выбор си с позиции обеспечения необходимой точности.

Определим суммарную погрешность отклонения от соосности в соответствии с разработанной схемой (СамГТУ.200501.059.12.03) по формуле:

Погрешность плиты - 6мкм, погрешность штатива – 4мкм, погрешность стойки - 4мкм, погрешность скалки - 2мкм. Тогда:

Для регистрации заданного допуска должно быть выбрано СИ, обладающее погрешностью не более 14,15мкм. Это может быть индикатор часового типа ИТ с погрешностью СИ , ценой деления 0,01.

1.6 Принцип действия выбранного си.

К зубчатым приборам, основанным на применении зубчатой передачи, относятся индикаторы часового типа ИЧ и ИТ, предназначенные для относительных измерений наружных размеров, отклонений формы и расположения поверхностей. Индикатор, кроме того, используют еще в качестве измерительного элемента в индикаторной скобе, индикаторном стенкомере, индикаторном глубиномере и некоторых других приборах. Настройку индикатора на нулевую отметку выполняют поворотом ободка с циферблатом вокруг оси, что избавляет от необходимости иметь микрометрическую подачу стола при измерении на стойке и удобно при контроле отклонений расположения и формы поверхностей. Кроме стрелки на лицевую сторону циферблата вынесен указатель числа ее оборотов, выполненный в виде малой стрелки.

Измерительный стержень (1) с зубчатой рейкой (2), перемещаясь, поворачивает триб (А₁=16), который жестко связан с зубчатым колесом (А₂=100) и вращается с ним на одной оси. Колесо находится в зацеплении с трибом (А₃= 10), на оси которого установлена стрелка (4). Зубчатое колесо (А₄=100), на оси которого неподвижно посажена втулка с волоском, находится в зацеплении с трибом (А₃=10). Колесо, находясь под действием волоска, заставляет всю передачу работать на одной стороне профиля зуба, вследствие чего устраняется мертвый ход. На оси колеса установлена стрелка - указатель числа оборотов соточной стрелки. Измерительное усилие создается пружиной.

Рис.4 Индикатор часового типа

2. Оценка достоверности контроля.

2.1 Понятие о вероятностных ошибках первого и второго рода. Причины их возникновения.

При выполнении контроля решение всегда принимается в условиях помех. Поэтому говорить о величине параметра можно лишь с некоторой вероятностью, при этом существуют так называемые вероятности ошибок:

- вероятность ошибки I рода (годная деталь признается браком);

- вероятность ошибки II рода (бракованная деталь признается годной). Тогда очевидно, что вероятность правильного решения о процедуре контроля (достоверность решения) составляет:

Оценка вероятностных ошибок осуществляется в области безразмерных величин. Введем обозначения:

 - безразмерная величина, характеризующая истинное значение погрешности контролируемого параметра, т.е. отклонение от номинального значения.

Очевидно, что при попадании параметра в допуск справедливо неравенство:

- безразмерная величина, пропорциональная текущей ошибке измерения (в данном случае находится пределах ).

При выполнении измерений на результате сказывается и величина отклонения параметра от номинала и ошибка средства измерения, т.е. формируется видимое значение контролируемого параметра, которое через безразмерные величины можно характеризовать как .

Величины ξ и η являются случайными и взаимонезависимыми, каждая из них характеризуется функциями распределения:

где - плотность распределения случайной величины .

где - плотность распределения случайной величины .

Совместная функция распределения суммы двух случайных величин и :

(1)

- совместная плотность распределения случайной величины.

Поскольку ξ и η являются взаимо независимыми случайными величинами, совместная плотность распределения может быть представлена:

Тогда соотношение (1) можно записать:

(2)

Ошибка I рода

Ошибка I рода имеет место при условии, что контролируемый параметр находится в поле допуска ξ ≤ 1, а видимые значения ξ + η > 1 фиксируют выход за пределы допуска

Область интегрирования G двумерной функции распределения в этом случае может быть отражена графически.

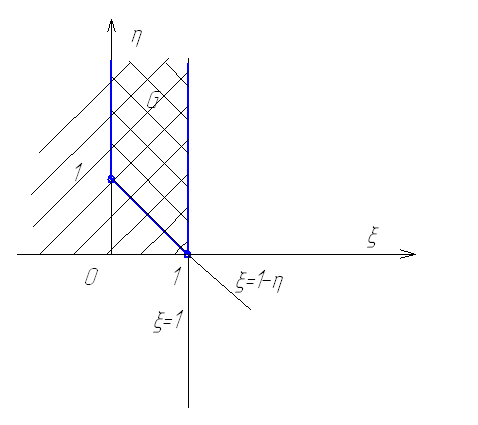
Рис.5 Распределения ошибки I рода

Из рисунка следует, что ошибка первого рода составляет:

Ошибка II рода

Ошибка II рода имеет место при условии

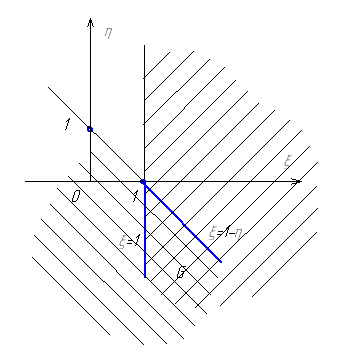
Рис.6 Распределения ошибки II рода

При оценке значений ошибок I и II рода в практических расчетах полагают, что ошибки измерений и погрешность контролируемого параметра распределены равномерно в некоторых определенных пределах.

Эта гипотеза обуславливает некоторую завышенность получаемых оценок.