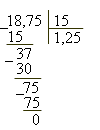1.2.2. Десятичные дроби

Дробь, знаменатель которой равен 10, 100, 1000 и вообще , может быть записана в виде десятичной дроби.

Например, Аналогично можно записывать неправильную дробь и смешанное число, например По сути, десятичное число – просто удобная форма записи дроби с указанными знаменателями.

Рассмотрим десятичную дробь 3,1415. Имеем:

Таким образом, в десятичной дроби 3,1415 содержится 3 единицы, 1 десятая, 4 сотых, 1 тысячная, 5 десятитысячных. Вообще, в десятичной дроби может быть сколько угодно разрядов: десятые, сотые, тысячные, десятитысячные, стотысячные и т. д.

Рассмотренную дробь можно записать так:

Но  а Таким образом, десятичная дробь не изменится, если к ней справа приписать любое количество нулей.

Ясно, что верно и обратное: десятичная дробь не изменится, если отбросить нули, стоящие справа в конце неё. Например, (нули, не стоящие в конце числа, отбрасывать нельзя).

Перечислим, как с десятичными числами можно проводить известные нам арифметические операции.

ложение и вычитание. Сложение и вычитание десятичных чисел производится точно так же, как сложение и вычитание целых чисел, нужно только записывать одноимённые разряды один под одним. Например,

Умножение. Умножение десятичных дробей проводится следующим образом. Перемножаем данные числа, как целые, не обращая внимания на запятые. Затем ставим в произведении запятую по следующему правилу: число знаков после запятой в произведении равно сумме чисел знаков после запятой во всех сомножителях. Заметим, что до постановки запятой отбрасывать знаки нельзя.

Пример 1

Вычислить 0,225 ∙ 0,04.

Решение

225 ∙ 4 = 900. Число знаков после запятой должно быть 3 + 2 = 5. Приписывая к 900 нули слева (00900), отделяем справа пять знаков. Получаем 0,09. Итак, 0,225 ∙ 0,04 = 0,09.

В частности, из этого правила следует, что десятичная дробь увеличится в 10, 100, 1000 и т. д. раз, если запятую перенести через один, два, три и т. д. разряда вправо.

Пример 2

Число 34,0945876 увеличится в 1000 раз, если мы напишем 34094,5876.

Десятичная дробь уменьшится в 10, 100, 1000 и т. д. раз, если запятую перенести через один, два, три и т. д. разряда влево.

Пример 3

Число 3409458,76 уменьшится в 100 раз, если мы напишем 34094,5876.

Деление. Деление десятичной дроби на натуральное число производится так же, как и натурального числа на натуральное. Запятую в частном ставят после того, как закончено деление целой части.

Пример 4

Разделить 18,75 : 15.

Решение

Итак, 18,75 : 15 = 1,25.

Если целая часть делимого меньше делителя, то в ответе получается нуль целых.

Пример 5

Разделить 0,806 : 31.

Решение

Итак, 0,806 : 31 = 0,026.

Для того чтобы разделить десятичную дробь (или целое число) на десятичное дробь, нужно отбросить запятую в делителе; в делимом же переносим запятую вправо на столько знаков, сколько их было в дробной части делителя (в случае необходимости в конце делимого приписывают нули). После чего делим полученное число на натуральное.

Пример 6

Разделить 9,43 : 0,23.

Решение

Итак, 9,43 : 0,23 = 41.

 

Пусть дана некоторая десятичная дробь, например 34,2741. Если приписать справа (после запятой) к ней любое число нулей, то, как известно, значение этой дроби не изменится:

Допустима также запись этой дроби с бесконечным количеством нулей: 34,274100...

Если у десятичной дроби после запятой содержится бесконечно много знаков, то такая дробь называется бесконечной десятичной дробью. Справедлива важная теорема: