3. Расчет тонкостенных конических сосудов

Радиус кривизны меридионального сечения ρ_m=0. Радиус кривизны ρ_θ переменный и выражается через радиус текущего поперечного сечения по формуле:

в

Рисунок 14.7 – Тонкостенный конический резервуар: а) – схема; б) эпюры напряжений (множитель при ординатах равен ); в) – отсеченная часть резервуара

При постоянном внутреннем давлении –p напряжения переменно по высоте резервуара

По формуле (14.4) находим σ_m

   

Задавая значения z, найдем меридиональные напряжения в различных точках резервуара. Максимальное значение меридиональных напряжений σ_m будет при. .

Из уравнения Лапласа получим:

Максимальное значение окружных напряжений σ_θ будет при z = H/2.

2. Особенности работы резервуаров сложного очертания

   Если стенки резервуара имеют резкий излом (рисунок 14.8), то в переходном сечении возникают краевые силы, которые могут вызвать значительные изгибные напряжения, не учитываемые безмоментной теорией. Чтобы уменьшить изгиб, в резервуарах устанавливают кольца жесткости, или распорные кольца, которые принимают на себя радиальные усилия q.

а) б)

Рисунок 14.8 - Место соединения цилиндрической и конической частей оболочки (а) и Усилия в ребрах жесткости (б)

Из условия равновесия полукольца, получаемого путем разреза ребра жесткости по диаметру, имеем . Если приближенно не учитывать совместной работы ребра и полки, то:

,

где – площадь поперечного сечения распорного кольца.

14.3.1 Пример расчета тонкостенного резервуара сложной формы

    Для стального резервуара, заполненного жидкостью (рисунок 14.9), необходимо:

1. Построить эпюры меридиональных и окружных напряжений;

2. Определить толщину стенок резервуара;

3. Найти размеры поперечного сечения распорного кольца.

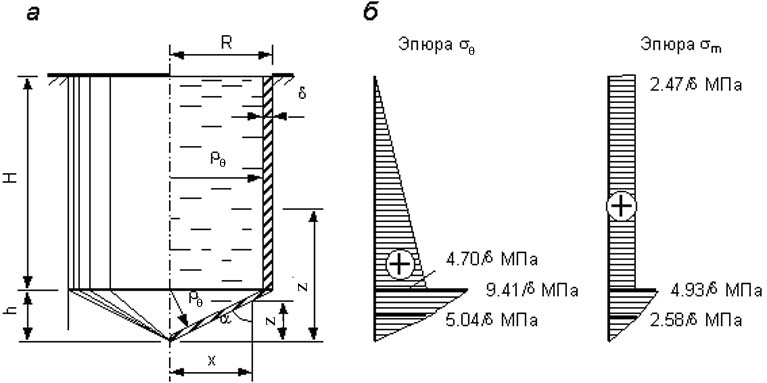Рисунок 14.9 - а – тонкостенный резервуар сложной формы; б – эпюры нормальных напряжений

Дано: γ =1,2 т/м³; Н=4 м; R =1 м; α=60^о; [σ] =100 MПа

Решение:

Для конической части резервуара

, м;

H+h=4+0,5774 = 4,5774 м.

Из уравнения Лапласа при .

На глубине (H+h-z) давление жидкости равно:

p=γ(H+h-z)= γ(4,5774-z),

тогда

γ =1,2 т/м³·9,8 м/с²=11,76кН/м³

при z = 0; σ_θ = 0;

при z= h/2 = 0,5774/2 = 0,2887 м

при z = h = 0,5774 см .

  Для цилиндрической части

,

.

При z = 4,5774 м

Эпюра окружных напряжений показана на рисунке 14.9,б. Для конической части эта эпюра параболическая. Её математический максимум имеет место в середине общей высоты при . При он имеет условное значение. При он попадает в пределы конической части и имеет реальное значение

Меридиональные напряжения σ_m определяется отдельно для цилиндрической и конической части резервуара, как это делалось для окружных напряжений. Для конической части резервуара вес жидкости в отсеченной части

,

давление верхних слоев жидкости . Подставляя эти выражения в формулу σ_m , получаем:

.

При z = 0, σ_m=0;

при z=h/2=0,5774/2= 0,2887 м

МПа;

при z= h = 0,5774 м МПа.

Максимальное значение σ_m для конической части, будет при . Реальное значение σ_m имеет только при , когда попадает в пределы конической части, и равно:

В цилиндрической части , ,

.

Подставляя эти выражения в формулу (14.4), получаем:

МПа.

    Эпюры меридиональных и окружных напряжений показаны на рисунке 14.9, б. По эпюрам видно, что опасным сечением является верхняя кромка конической части резервуара, при

МПа, МПа;

и откуда мм.

Округляя, принимаем δ= 1мм.

Площадь поперечного сечения распорного кольца резервуара будет:

см²

В качестве распорного кольца используем равнополочный уголок 56х 56х 4 (ГОСТ 2509-86) площадью 4,38 см².