14.1. Определение напряжений в тонкостенной оболочке

Определим по безмоментной теории напряжения в стенке оболочки от внутреннего давления р.

Рисунок 14.1 – Тонкостенная осесимметричная оболочка

Из стенки сосуда (рисунок 14.1,а) вырежем мысленно двумя меридиональными и двумя нормальными коническими сечениями прямоугольный элемент аbcd с криволинейной поверхностью размерами dS₁ и dS_2. Обозначим главные радиусы кривизны срединной поверхности элемента в меридиональной плоскости ρ_m,, а радиусы кривизны в плоскости, перпендикулярной к меридиану ρ_Θ ; меридиональные напряжения - через σ_m и окружные σ_θ; углы соответственно dφ и dθ. Третье главное напряжение, перпендикулярное к элементу внутри сосуда обозначим через р, снаружи давление равно нулю. При этом условии напряженное состояние стенки сосуда является плоским.

а) б)

Рисунок 14.2 - Напряженное состояние тонкостенной оболочки

Рассмотрим условие равновесия элемента (рисунок 14.2). На элемент действуют следующие силы: по касательной к меридиану σ_mδdS₂; по касательной к окружности σ_θδdS₁; перпендикулярно к элементу pdS₁dS₂ (рисунок 14.2,а). Составим уравнение равновесия выделенного элемента, приравняв нулю сумму проекций всех сил на нормаль к элементу:

(14.1)

учитывая, что Sin(dθ/2)≈ (dθ/2); Sin(dφ/2)≈ (dφ/2), и выразив dθ и dφ через отношение dθ=dS₂/ρ_θ и dφ=dS1/ρ_m, получим:

(14.2)

Полученное выражение носит название уравнения Лапласа. Уравнение содержит две неизвестные величины σ_m и σ_θ. Для их определения составим второе уравнение, которое можно получить, рассмотрев равновесие отсеченной части сосуда (рисунок 14.1,б). Из уравнения суммы проекций всех сил на вертикальную ось определим σ_m.

, (14.3)

Откуда

  ,              (14.4)

где Q– вес части сосуда и жидкости, лежащий ниже рассматриваемого окружного сечения; P– давление жидкости, равное (γ– объемный вес жидкости, h– глубина рассматриваемой точки). Если жидкость находится под давлением q, то P=γh+q.  Уравнения (14.2) и (14.4) позволяют найти напряжения σ_m и σ_θ в любой точке сосуда.

14.2 Частные случаи расчета тонкостенных сосудов

14.2.1. Сферический сосуд под действием равномерного

внутреннего давления

В случае сферического сосуда задача определения напряжений решается только с использованием уравнения Лапласа.

Рисунок 14.3 –

Сферическая оболочка

Рисунок 14.4 –

Цилиндрическая оболочка

Если сфера имеет диаметр D, то ρ_θ = ρ_m =R =D/2. Очевидно также, что σ_m= σ_θ. Тогда из уравнения Лапласа находим:

(14.5)

14.2.2 Цилиндрический сосуд под действием

равномерного внутреннего давления

Рассмотрим цилиндрический сосуд диаметром D с днищами. Радиусы кривизны ρ_θ = R; ρ_m =∞. Из уравнения Лапласа можно определить только окружное напряжение

(14.6)

откуда

(14.7)

 

в)

   В сферической части цилиндрического сосуда напряжения можно определить как для сферических сосудов (14.5), приняв в качестве радиуса R₁.

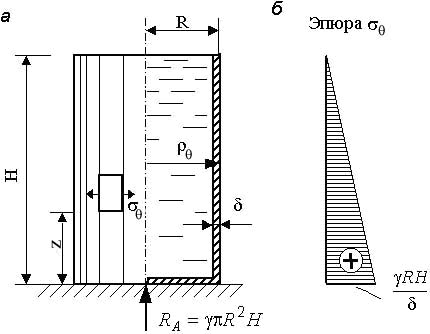
Рисунок 14.5 – Тонкостенный цилиндрический резервуар

и эпюры напряжений

Для цилиндрического резервуара (рисунок 14.5)

ρ_θ = R; ρ_m =∞; α=0, Cos α=1, p=γ(H-z), Q=(πR²z)γ.

Из уравнения Лапласа

откуда

при z = 0, ;

при z = H, σ_θ = 0

На рисунке 14, б показаны эпюры меридиональных и окружных напряжений в резервуаре.

    Если резервуар опирается днищем (рисунок 14.6), то распределение напряжений σ_m и σ_θ будет несколько иным. Из уравнения проекций на вертикаль для отсеченной части (рисунок 14.6) получаем:

в

Рисунок 14.6 – Тонкостенный цилиндрический резервуар с днищем: а) - схема; б) - эпюра окружных напряжений; в) – отсеченная часть резервуара

;

;

;

;

Из уравнения Лапласа:

, откуда

при              z = 0              ;

при              z = H                .

Эпюра σ_θ показана на рис.14.6,б.