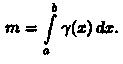Применение формулы Тейлора при вычислении предела функции

Формула Тейлора

 

 Формулы Тейлора часто применяют для приближенного вычисления значений функции и о(хn) указывает степень точности вычисления.

Чтобы пользоваться формулой Тейлора, надо знать вид формулы Тейлора для основных элементарных функций:

Следует помнить, что применять формулы (4.1.) или 1-10 можно для функции   только в случае, если  при .

 

Эквивалентные бесконечно малые. Применение эквивалентности при вычислении пределов функций.

 3.1. Определение 1. Функция  называется бесконечно малой при  (или ), если  (или ).

Так как , то при   -бесконечно малая. Однако  не является бесконечно малой при , так как  Одна и та же функция может быть бесконечно малой или не быть в зависимости от предельного значения x0. Есть функции, например x2+1, которые не могут быть бесконечно малыми ни при каких условиях. Вычисление определенного интеграла Пусть в интеграле  нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.

Определение 2. Две бесконечно малые называются эквивалентными, если предел их отношения равен 1.

 

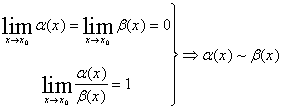
При вычислении пределов часто применяется следующая Теорема. Предел отношения двух бесконечно малых (неопределенность ) равен пределу отношения двух других бесконечно малых, эквивалентных данным, т.е.

 

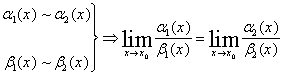
Отметим также: если , то .

14.---------------------------------------------------------------------------------------------------------------

Рассмотрим задачу, обратную задаче нахождения производной от заданной дифференцируемой функции: найти F(x), если известны ее производная или дифференциал Физический смысл такой задачи можно пояснить следующим примером: по заданной скорости неравномерного прямолинейного движения найти его закон s(t).

О: Функция F(x) называется первообразной для (х) на открытом или закрытом промежутке X, если

Пример:

Т.1: (теорема существования) Любая непрерывная на X функция имеет первообразную F(x) на X:

Функция на X может иметь бесконечно много первообразных. Так, для первообразной является F(x) =

Т.2: Если F(x) и — две первообразные для (х) на X, то

разность между ними равна постоянной Обозначим тогда

Пусть Применим теорему Лаг-

ранжа для на

откуда на X

Следствие. Если F{x) — первообразная для (х) на X, то F(x) + c, c = const — множество всех первообразных для (х).

О: Неопределенным интегралом (н.и.) от функции

называется совокупность всех первообразных этой функции.

Обозначение н.и.:

Функцию (х) называют подынтегральной функцией, —

подынтегральным выражением, нахождение н.и. от функции — интегрированием

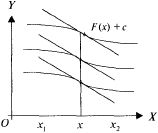
Рис. 15.1

Геометрический смысл н.и. следует из геометрического смысла производной: уравнение y=F(x) +с на плоскости ХОY определяет семейство кривых (называемых интегральными кривыми), для которых в точке с абсциссой х угловой коэф-фициент касательных равен )

(рис.15.1). Физический смысл н.и.: т.е. н.и. от скорости неравномерного прямолинейного движения дает зависимость пути от времени.

Свойства первообразной

• Первообразная суммы равна сумме первообразных

• Первообразная произведения константы и функции равна произведению константы и первообразной функции

• Достаточным условием существования первообразной у заданной на отрезке функции является непрерывность на этом отрезке

• Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу

• У заданной на отрезке функции любые две первообразные отличаются на постоянную.

15.-----------------------------------------------------------------------------------------------------------------

метода замены переменных в неопределенном интеграле.

Пример 5

Найти неопределенный интеграл.

В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже  говорили, для решения интеграла нам приглянулась табличная формула , и всё дело хотелось бы свести к ней.

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой. В данном случае напрашивается: Вторая по популярности буква для замены – это буква . В принципе, можно использовать и другие буквы, но мы всё-таки будем придерживаться традиций.

Итак: 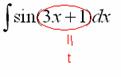Но при замене у нас остаётся ! Наверное, многие догадались, что если осуществляется переход к новой переменной , то в новом интеграле всё должно быть выражено через букву , и дифференциалу  там совсем не место. Следует логичный вывод, что  нужно превратить в некоторое выражение, которое зависит только от .

Действие следующее. После того, как мы подобрали замену, в данном примере,  , нам нужно найти дифференциал . С дифференциалами, думаю, дружба уже у всех налажена.

Так как , то

После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко: Теперь по правилам пропорции выражаем нужный нам :

В итоге: 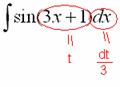  Таким образом: А это уже самый что ни на есть табличный интеграл  (таблица, интегралов, естественно, справедлива и для переменной ).

В заключении осталось провести обратную замену. Вспоминаем, что .

Готово.

Чистовое оформление рассмотренного примера должно выглядеть примерно так:

“

Проведем замену:

“

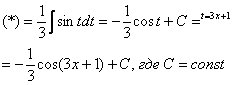Значок  не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений.

Также всем рекомендую использовать математический знак  вместо фразы «из этого следует это». И коротко, и удобно.

При оформлении примера в тетради надстрочную пометку   обратной замены лучше выполнять простым карандашом.

Внимание! В следующих примерах нахождение дифференциала  расписываться подробно не будет.

А теперь самое время вспомнить первый способ решения:

В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче. Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.

Пример 6

Найти неопределенный интеграл.

Проведем замену:  (другую замену здесь трудно придумать)

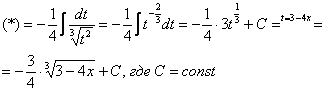
Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.

Ленивые продвинутые люди запросто решат данный интеграл методом подведения функции под знак дифференциала:

Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении.

Пример 7

Найти неопределенный интеграл. Выполнить проверку. Это пример для самостоятельного решения. Ответ в конце урока.

Пример 8

Найти неопределенный интеграл.

Замена: Осталось выяснить, во что превратится Хорошо,  мы выразили, но что делать с оставшимся в числителе «иксом»?! Время от времени в ходе решения интегралов встречается следующий трюк:  мы выразим из той же замены !

Готово.

Пример 9

Найти неопределенный интеграл. Это пример для самостоятельного решения. Ответ в конце урока.

Пример 10

Найти неопределенный интеграл.

Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.

Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функция и её производная :  (функции ,  могут быть и не в произведении)

В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.

В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу , которая как раз понижает степень на единицу. А, значит, если обозначить за  знаменатель, то велики шансы, что числитель  превратится во что-нибудь хорошее.

Замена:

Кстати, здесь не так сложно подвести функцию под знак дифференциала:

Следует отметить, что для дробей вроде ,  такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей.

Вот еще пара типовых примеров для самостоятельного решения из той же оперы:

Пример 11

Найти неопределенный интеграл.

Пример 12

Найти неопределенный интеграл.

Решения в конце урока.

Пример 13

Найти неопределенный интеграл.

Смотрим в таблицу производных и находим наш арккосинус: . У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную.

Общее правило: За  обозначаем саму функцию (а не её производную).

В данном случае: . Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения .

В этом примере нахождение  я распишу подробно поскольку  – сложная функция.

Или короче: По правилу пропорции выражаем нужный нам остаток:

Таким образом:

Вот здесь подвести функцию под знак дифференциала уже не так-то просто.

Пример 14

Найти неопределенный интеграл.

Интегрирование по частям

Пусть надо вычислить интеграл вида

∫  U(x) · v(x) dx ,

где   v(x)  имеет очевидную первообразную   V(x).

Тогда

∫  U(x) · v(x) dx   =   ∫  U(x) · V'(x) dx   =   ∫  U(x)  dV(x) .

Такого рода преобразование называется подведением под знак дифференциала, поскольку функция v(x) исчезает в интегрируемом выражении и появляется под знаком дифференциала в виде своей первообразной V(x).

Если функция U(x) выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то

∫  U(x)  dV(x)   =   ∫  w(V(x)) dV(x)   =   ∫  w(t) dt ,

где t = V(x). Таким образом отыскание исходного интеграла сводится к отысканию интеграла

∫  w(t) dt

В нем функция t = V(x) выступает как независимая переменная, т.е. произошла замена переменной.

Если функция U(x) не выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то может оказаться полезным преобразование, называемое интегрированием по частям. Оно определяется следующей теоремой.

Теорема 1. Пусть функции U(x) и V(x) дифференцируемы на некотором интервале и на этом интервале существует интеграл   ∫ V(x)U '(x)  dx .

Тогда существует интеграл   ∫ U(x)V '(x)  dx и справедлива формула

∫ U(x)V '(x)  dx   =   U(x)V(x)   −   ∫ U '(x)V(x)  dx.

(1)

Доказательство следует из формулы дифференцирования произведения. Оно приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 168.

Замечание 1. Очевидно, что в формуле интегрирования по частям оператор дифференцирования, обозначенный штрихом, перемещается с V на U. Этим обусловлена важная роль формулы при доказательстве самосопряженности линейных дифференциальных операторов.

Замечание 2. Формулу интегрирования по частям удобно применять также в виде

∫ U(x) · v(x) dx   =   U(x) · V(x) − ∫ u(x) · V(x) dx,

(2)

где функция v(x) имеет очевидную первообразную V(x) , а   U(x) — дифференцируемая функция, причем ее производная   u(x) = U'(x)  является более простой функцией, чем она сама.

Замечание 3. Формулу интегрирования по частям (1) можно представить в виде в виде

∫ U(x) dV(x)   =   U(x)V(x)   −   ∫ V(x) dU(x) .

(3)

Метод интегрирования по частям применяется в следующих случаях:

1. Подынтегральное выражение содержит в качестве множителя одну из функций ln x ,   arcsin x ,   arccos x ,   arctg x . Если применить формулу (2), полагая в ней U(x) равной одной из этих функций, то подынтегральное выражение Vxu(x) может оказаться проще исходного.

2. Подынтегральное выражение имеет вид:   Pn(x) eαx ,    Pn(x)sinαx или   P(x)cosαx ,  где Pn(x) — многочлен степени n .

Интегралы от таких функций вычисляются n –кратным применения формулы интегрирования по частям (1), причем в качестве U(x) каждый раз следует брать многочлен. После каждого интегрирования по частям степень многочлена понижается на единицу.

3. Подынтегральное выражение имеет вид

eαx · cosβx,  eαx · sinβx,  sin(lnx),  cos(lnx).

После двукратного интегрирования по частям получается линейное алгебраическое уравнение относительно исходного интеграла.

4. После подведения под знак дифференциала получился интеграл   ∫ U(x) dV(x) ,   в котором функция U(x) не выражается через V(x), но функция V(x) выражается через U(x). Тогда можно применить формулу интегрирования по частям (3).

16.-----------------------------------------------------------------------------------------------------------------

Понятие определенного интеграла

1. Площадь криволинейной трапеции.

Пусть функция  f(x)  непрерывна на отрезке  [a, b ]  и неотрицательна, т.е.  f(x) ≥ 0  при всех  x О   [ a, b]. Рассмотрим фигуру, ограниченную графиком функции  y = f(x )  и прямыми  x = a,  x = b,  y = 0  (рис. 1).

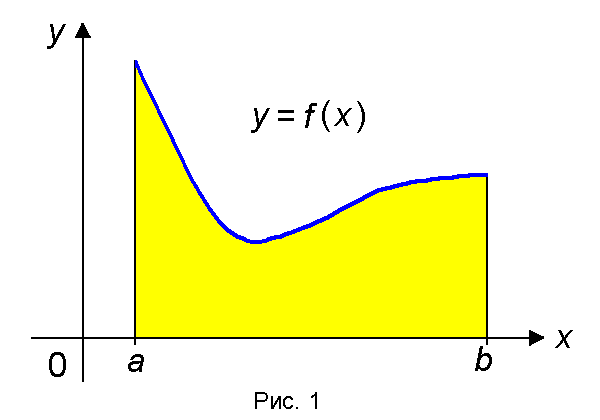
Такую фигуру называют криволинейной трапецией.

Наша задача — дать определение и указать способ вычисления площади криволинейной трапеции. Для этого произвольно разобьем отрезок  [a, b ]  на n отрезков точками

x0 = a < x1   … < xk − 1 < xk < … < xn − 1 < xn = b.

(1)

Проведем через эти точки прямые, параллельные оси OY.

Тогда криволинейная трапеция разобьется на n частей, каждая из которых является криволинейной трапецией.

Введем обозначения

Δxk = xk − xk − 1  (k = 1,…,n);    λ = max 1 ≤ k ≤ n Δxk.

(2)

На каждом отрезке  [x k − 1, x k ]  выберем произвольным образом точку  ξk  (k = 1, …,n).

Рассмотрим фигуру, состоящую из прямоугольников с основаниями  Δxk  и высотами   f(ξk).  (рис. 2)

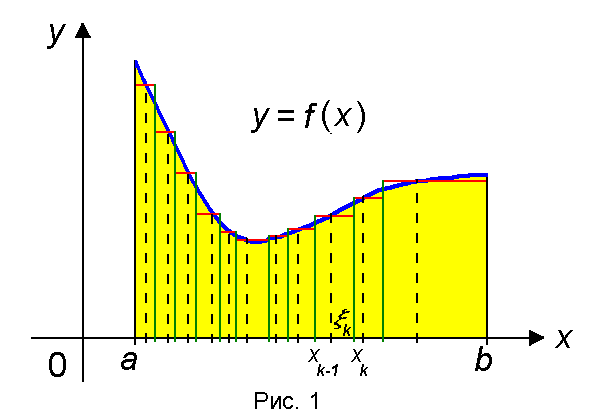
Площадь  Sn  этой фигуры вычисляется по формуле

Sn =   n f(ξk) Δxk ∑ k = 1 .

Очевидно, что при достаточно малых отрезках  Δxk  эта фигура будет мало отличаться от исходной криволинейной трапеции. Поэтому за площадь S криволинейной трапеции естественно принять предел площадей таких фигур при стремлении к нулю длин всех отрезков разбиения

S = lim λ → 0 Sn = lim λ → 0 n f(ξk) · Δxk ∑ k = 1

(3)

(при условии, что указанный предел существует и не зависит ни от способа разбиения отрезка  [a, b]  на части, ни от выбора точек  ξk).

2. Понятие определенного интеграла

Пусть функция  f(x)  определена на отрезке  [a,  b].  Разобьем отрезок  [a, b ]  на n отрезков точками

x0 = a < x1 < … < xk − 1 < xk < … < xn − 1 < xn = b

и введем обозначения

Δxk = xk − xk − 1  (k = 1, …,n);    λ = max 1 ≤ k ≤ n Δxk.

На каждом отрезке  [x k − 1, x k]  выберем произвольным образом точку  ξk  (k = 1, …,n)  и составим сумму

n ∑ k = 1 f(ξk) · Δxk ,

(5)

называемую (римановой) интегральной суммой функции  f(x)  на отрезке  [a, b ].

Если существует конечный предел интегральных сумм (5) при  λ → 0,  причем этот предел не зависит ни от способа разбиения отрезка  [a , b]  на части, ни от выбора точек  ξk,  то функция  f(x)  называется интегрируемой (по Риману) на отрезке  [a, b ],  а указанный предел называется (римановым) определенным интегралом от   f(x)  по отрезку  [a, b ]  и обозначается символом

b ∫ a f(x) dx .

Таким образом,

b ∫ a f(x)  dx   = lim λ → 0 n ∑ k = 1 f(ξk) · Δxk .

Замечание. Данное Риманом определение интеграла оказалось неудачным. Современная терия интегрирования опирается на определение, данное Лебегом. Она гораздо более мощная и простая в применениях, чем теория Ремана.

3. Необходимое условие интегрируемости

Теорема 1. Если функция  f(x) интегрируема на отрезке  [a,  b],  то она ограничена на этом отрезке.

Доказательство приведено в книге И.М. Петрушко, Л.А. Кузнецова, В.И. Прохоренко, В.Ф. Сафонова “Курс высшей математики : Интегральное исчисление. Функции нескольких переменных. Дифференциальные уравнения”. М. : Изд–во МЭИ, 2002. (Стр. 41.)

Замечание. Ограниченность функции не является достаточным условием ее интегрируемости.

Достаточные условия интегрируемости

Теорема 2. Если выполнено одно из следующих условий :

• функция  f(x)  непрерывна на отрезке  [a, b ];

• функция  f(x) ограничена на отрезке  [a, b]  и имеет на этом отрезке конечное число точек разрыва;

• функция  f(x)  монотонна на отрезке  [a, b],

то  f(x)  интегрируема на отрезке  [a, b] и, следовательно,

b ∫ a   f(x)  dx

существует.

4. Геометрический смысл определенного интеграла

Из теоремы 2 и формулы (3) следует, что если функция  f(x) непрерывна и неотрицательна на отрезке  [a,  b],  то площадь S криволинейной трапеции, ограниченной графиком функции  y = f(x)  и прямыми  x = a,  x = b,  y = 0  (рис. 1), вычисляется по формуле

S =   b ∫ a   f(x)  dx .

Площадь криволинейной трапеции

Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Д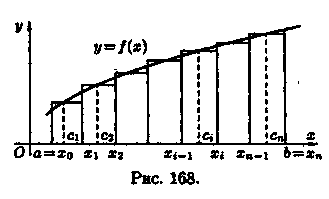 ля этого отрезок [а; b] точками а=х₀, х₁, ..., b=х_n (х₀<x₁<...<x_n) paзобьем на n частичных отрезков [х_о;х₁], [х₁;х₂],...,[х_n-1;х_n]. (см. рис. 168). В каждом частичном отрезке [x_i-1;x_i] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(c_i).

Умножим значением функции ƒ(c_i) на  длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка. Произведение ƒ(c_i) • ∆x_i равно площади прямоугольника с основанием ∆x_i и высотой ƒ(c_i). Сумма всех таких произведений

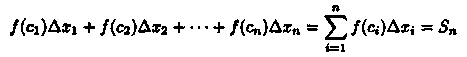
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

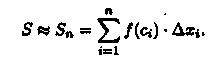
С уменьшением всех величин Δх_i точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры S_n, когда n неограниченно возрастает так, что λ = max∆x_i →0:

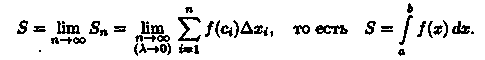
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла.

Работа переменной силы

Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.

Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а < b). Для этого отрезок [а; b] точками а = х₀, х₁, ..., b = х_n (х₀ < x₁ < ... < х_n) разобьем на n частичных отрезков [х₀; x₁], [x₁; x₂],..., [x_n-1; x_n]. Сила, действующая на отрезке [x_i-1; x_i], меняется от точки к точке. Но если длина отрезка Δхi = х_i-x_i-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = c_i  [x_i-1; x_i]. Поэтому работа, совершенная этой силой на отрезке [x_i-1;x_i], равна произведению F(c_i)•Δх_i (Как работа постоянной силы F(c_i) на участке [x_i-1; x_i].)

Приближенное значение работы А силы F на всем отрезке [а; b] есть

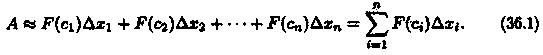
Это приближенное равенство тем точнее, чем меньше длина Δх_i Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

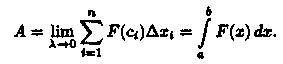
Итак, работа переменной силы F , величина которой есть непрерывная функция F = F(x), действующей на отрезке [а; b], равна определенному интегралу от величины F(x) силы, взятому по отрезку [а; b].

В этом состоит физический смысл определенного интеграла.

Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t=а до t=b, равен определенному интегралу от скорости v(t):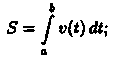

масса m неоднородного стержня на отрезке [a,b] равна определенному интегралу от плотности (х):