Bilety_bakal_10-11

Кам’янець-Подільський національний університет імені Івана Огієнка

Галузь знань 0403 Системні науки та кібернетика

Напрям підготовки 6.040302 Інформатика

Державний екзамен державний іспит за напрямом підготовки

ЕКЗАМЕНАЦІЙНИЙ БІЛЕТ № __

1. Потужність множини. Зчисленні та незчисленні множини. Їх властивості.

2. Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.

3. З десяти лотерейних білетів 3 виграшні. Визначити ймовірність того, що серед чотирьох взятих навмання білетів хоч один виграшний.

4. Визначити, яка рівність точніша 5/3=1,67 чи

1. Лінійні простори, означення та властивості. Приклади лінійних просторів.

2. Алгоритм. Способи опису алгоритмів. Словесна та графічна форми подання алгоритмів.

3. Серед 30 екзаменаційних білетів 5 «щасливих». Два студенти по черзі беруть по одному білету. Яка імовірність того, що другий студент взяв щасливий білет.

4. Розв'язати систему рівнянь, використовуючи правила підрахунку цифр

1. Похідна функції однієї змінної, її геометричний та механічний зміст. Основні правила диференціювання.

2. Величини. Концепція типів даних у мові програмування.

3. Першість України з футболу виборюють 16 команд, серед яких5 провідних. Команди поділено на дві підгрупи по 8 команд. Яка імовірність того, що всі провідні команди потраплять в одну підгрупу.

4. Відокремити корені і уточнити один з них методом половинного ділення (2-3 кроки)

.

1. Диференційовані функції однієї змінної, критерій диференційованості. Диференціал в точці, його геометричний зміст, застосування до наближених обчислень.

2. Програма. Поняття мови програмування. Поняття про середовище програмування.

3. В квадрат вписано коло. Знайти імовірність того, що точка, кинута в квадрат, потрапить в круг.

4. Перевірити чи буде збіжним ітераційний метод для даної системи рівнянь

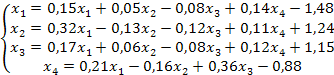
1. Основні теореми диференціального числення. Теорема Лагранжа. Умови сталості та монотонності функції.

2. Трансляція та її види: інтерпретація, компіляція. Їх особливості. Поняття системи програмування.

3. Розв’язати рівняння:

;

4. Студент прийшов на екзамен, знаючи лише 20 запитань з 30. Знайти імовірність того, що він відповість на всі три запитання білета.

1. Екстремум функції. Необхідні умови екстремуму. Достатні умови екстремуму.

2. Основні принципи технології структурного програмування. Метод покрокової деталізації.

3. Розв’язати рівняння:

4. Серед 18 деталей є 6 нестандартних. Навмання беруть 4 деталі. Випадкова величина  – число стандартних деталей у вибірці. Побудувати закон розподілу цієї величини. Обчислити її математичне сподівання та дисперсію.

1. Первісна функція та неозначений інтеграл. Інтегрування підстановкою та частинами.

2. Основні принципи технології об’єктно-орієнтованого програмування. Поняття про об’єкт (клас).

3. Розв’язати рівняння:

.

4. Знайти аналітичний вираз параболи, що проходить через точки

х	0	1	3	5
у	6	0	3	–1

1. Означений інтеграл. Необхідна умова інтегровності. Критерій інтегровності. Інтегровність неперервної функції.

2. Функції у мові С. Фактичні та формальні параметри.

3. Розв’язати рівняння:

4. Обчислити, використовуючи метод меж:

, якщо НМt=27,9; ВМt=28,5; НМs=7,44; ВМs=7,47

1. Квадровні фігури. Застосування означеного інтеграла до обчислення площ плоских фігур.

2. Алгоритми обробки масивів. Алгоритм послідовного пошуку. Пошук максимального (мінімального) елемента.

3. Знайти часткові розв’язки:

, .

4. Обчислити інтеграл з кроком h=0,2 за правилом трапеції.

1. Спрямлювані криві та їх довжини. Теорема Жордана. Обчислення довжини кривої за допомогою означеного інтеграла.

2. Алгоритми обробки масивів. Алгоритм бінарного пошуку.

3. Знайти часткові розв’язки:

, .

4. Методом штучного базису розв’язувати задачу лінійного програмування

min z = 2x₁ +5x₂ - 6x₃

x₁ - 2x₂ + 2x₃ = 4,

-x₁ + 3x₂ +2 x₃ = 2,

1. Застосування визначеного інтеграла до обчислення об’ємів тіл обертання та площ поверхонь обертання.

2. Лінійне програмування (ЛП). Приклади задач лінійного програмування (ЗЛП). Загальна та канонічна форми запису ЗЛП. Ознака оптимальності базисного допустимого розв’язку ЗЛП. Ознака необмеженості цільової функції ЗЛП на допустимій множині. Симплекс-метод розв’язування ЗЛП.

3. Знайти часткові розв’язки:

, , .

4. Перевірити справедливість формули

.

1. Додатні числові ряди, властивості збіжних рядів, критерій збіжності. Теореми про порівняння рядів. Ознака Даламбера та інтегральна ознака Коші.

2. Метод штучного базису відшукання початкового базисного розв’язку ЗЛП. М-метод розв’язування ЗЛП.

3. Розв’язати систему рівнянь:

, .

4. Задана система пропозиційних змінних {А, В, С}. Звести до Дднф формулу .

1. Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди.

2. Двоїсті ЗЛП та їх властивості. Теореми двоїстості. Двоїстий симплекс-метод.

3. Задана матриця А(10×15). Визначити й надрукувати на дисплей суму та кількість додатних елементів кожного стовпця і рядка матриці, по бажанню користувача. Результати віддрукувати у вигляді двох рядків.

4. Перевірити, чи (AB)C = (AB)(AC).

1. Функціональні послідовності і ряди. Збіжність, область збіжності. Рівномірна збіжність. Ознака Вейєрштраса.

2. Транспортна задача (ТЗ). Властивості ТЗ. Деякі методи відшукання початкового базисного розв’язку ТЗ. Метод потенціалів розв’язування ТЗ.

3. Задана матриця S(24×8). Обчислити середнє арифметичне елементів кожного рядка матриці і записати його в 8-й стовпець. Обчислити середнє арифметичне елементів кожного стовпця матриці і записати його в 24-й рядок. Надрукувати отриману матрицю.

4. Показати, що відношення „подібності трикутників” на множині трикутників площини є відношенням еквівалентності.

1. Метричні простори. Відкриті та замкнуті множини, їх властивості.

2. Потоки та мережі. Постановка задачі. Задача про найкоротший шлях. Метод Мінті. Задача про максимальний потік. Метод Форда-Фалкерсона.

3. Обчислити корені заданих квадратних рівнянь: , визначити, яке рівняння з даних має більшу суму коренів.

4. Скільки парних п’ятицифрових чисел можна утворити з парних цифр.

1. Векторний добуток двох векторів, його властивості та застосування.

2. Поняття границі числової послідовності, її властивості. Теорема про границю монотонної числової послідовності. Теорема Больцано-Вейєрштраса.

3. Задані одновимірні масиви X(100) та Y(100), які містять відповідні координати точок площини. Необхідно підрахувати кількість точок, що належать колу з радіусом R.

4. М-методом розв'язати задачу лінійного програмування:

max z = 2x₁ +4x₂+4x₃ -3 x₄

x₁ + x₂ + x₃ = 4,

x₁ + 4x₂ - x₃ + x₄ = 8,

1. Еліпс, означення та канонічне рівняння. Досліджен­ня форми еліпса за канонічним рівнянням.

2. Матрична гра. Оптимальні чисті стратегії. Критерії існування розв’язку матричної гри у чистих стратегіях. Оптимальні змішані стратегії та їх відшукання за допомогою ЛП. Існування розв’язку матричної гри у змішаних стратегіях (теорема про мінімакс).

3. Задані координати вершин трикутників масивами: XA(5),XB(5), XC(5),YA(5),YB(5),YC(5). Визначте периметри та площі трикутників, які можна утворити з заданих точок.

4. Встановити скільки є тризначних чисел, які не діляться ні на п’ять ні на сім.

1. Означення детермінанта n-го порядку. Властивості детермінантів.

2. Правила суми і добутку. Розміщення, перестанов­ки, комбінації (без повторень та з повтореннями).

3. Переставити перші M елементів в кінець лінійного масиву розмірністю N (M вводиться з клавіатури, M<N).

4. Двоїстим симплекс-методом розв’язати задачу лінійного програмування:

min z = 4x₁ + 5x₂

3x₁ + x₂ 3,

8x₁ + 4x₂1,

1. Розв’язування систем лінійних рівнянь методом Гауса.

2. Алгоритми обробки масивів. Сортування елементів масиву методом "бульбашки".

3. Написати програму, що друкує у напрямку спадання усі дільники введеного числа

4. Знайти перший базисний розв’язок методами північно-західного кута та мінімальної вартості та оптимізувати їх методом потенціалів для транспортної задачі

	10	20	5	25
25	2	1	4	5
18	2	2	4	1
17	2	3	1	3

1. Площини та прямі в просторі.

2. Теорема множення ймовірностей. Незалежність подій.

3. Написати програму, яка визначає, до якого типу відноситься чотирикутник із довжинами сторін a,b,c,d – прямокутник (паралелограм), квадрат (ромб), трапеція, довільний чотирикутник.

4. Розв'язати методом Форда-Фалкерсона задачу про максимальний потік на мережі, умова якої задана матрицею суміжності С і пропускних здатностей R:

1. Поверхні другого порядку. Еліпсоїди, параболоїди, гіперболоїди, гіперболічний параболоїд.

2. Формула повної ймовірності та формули Байєса.

3. Скласти програму, яка визначає, чи можна побудувати трикутник за заданими довжинами сторін a,b,c; якщо так, визначити, яким він є - гострокутним, прямокутним, різностороннім, рівнобедреним, рівностороннім.

4. Першим методом Гоморі розв’язати задачу цілочислового програмування

max z = 16x₁ +9 x₂

5x₁ + 2x₂  20,

x₁ + x₂  6,

x₁  0, x₂  0

x₁, x₂ – цілі.

1. Лінійні оператори, означення та властивості. Приклади лінійних операторів. Матриці лінійних операторів.

2. Опис рядків у мові програмування С. Операції над рядками, функції для обробки рядків.

3. Задано текстовий файл , який містить інформацію про дату народження кожного студента групи. Склад запису: прізвище студента<пропуск>дата народження(у форматі ДД.ММ.РРРР). Організувати пошук та вивід інформації про студентів які народилися у вказаному місяці.

4. Знайти оптимальні змішані стратегії та ціну матричної гри 22, заданої матрицею:

1. Множини та відношення. Основні види бінарних відношень. Розбиття множини на класи.

2. Динамічні структури даних. Поняття про стек, чергу, деку

3. У півкруг одиничного радіуса вписати прямокутник найбільшої площі, одна із сторін якого лежить на діаметрі кола.

4. Розв'язати квадратичним симплекс-методом таку задачу:

min Z = -5x₁ - 2x₂ + x₁² - x₁x₂ + x₂²

при обмеженнях

2x₁ + 3x₂  15,

x₁  0, x₂  0.

1. Лінійні диференціальні рівняння першого порядку та рівняння Бернуллі.

2. Канонічні (нормальні) форми булевих функцій. Алгебра Жегалкіна.

3. Дослідити на збіжність степеневий ряд

.

4. Обчислити, яку роботу виконує сила = (5; 5; 2), коли точка її прикладання рухається з початку в кінець вектора = (2; -3; -3).

1. Лінійні однорідні диференціальні рівняння n-го порядку із змінними коефіцієнтами. Фундаменталь­на система розв’язків. Детермінант Вронського. Загальний розв’язок.

2. Однонаправлені та двонаправлені лінійні списки. Включення елемента до лінійного однонаправленого списку.

3. Дослідити на екстремум функцію

.

4. Скласти рівняння площини, яка проходить через точку A(1; 2; 3) і має нормальний вектор = (3;2;1).

1. Системи лінійних диференціальних рівнянь із змінними коефіцієнтами. Визначник Вронського. Знаходження розв’язків неоднорідної системи.

2. Бінарні дерева. Вставка елемента у бінарне дерево.

3. Знайти площу фігури, яка обмежена кривою

.

4. Розв’язати за правилом Крамера систему рівнянь

1. Чисельні методи розв’язування нелінійних рівнянь.

2. Комбінаторні конфігурації. Біноміальна та поліноміальна теореми.

3. Знайти границю функції

.

4. Скласти канонічне рівняння гіперболи, якщо точка (-1,25; 1,5) належить гіперболі, а асимптотами є прямі .

1. Розв’язування диференціальних рівнянь та їх систем.

2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.

3. Дослідити функцію і побудувати її графік .

4. Розв’язати систему рівнянь методом Гаусса

1. Інтерполювання функцій многочленами Лагранжа.

2. Маршрути в графах. Алгоритми пошуку маршруту. Ейлерові та гамільтонові графи. Алгоритм пошуку ейлеревого шляху.

3. Дослідити на збіжність числовий ряд .

4. Знайти власні значення і власні вектори лінійного оператора, заданого матрицею

.

1. Лінійна та нелінійна кореляція. Метод найменших квадратів. Побудова емпіричних формул.

2. Опукле програмування. Функція Лагранжа. Теорема Куна-Таккера-1. Теорема Куна-Таккера-2. Задача опуклого квадратичного програмування. Квадратичний симплекс-метод.

3. Обчислити .

4. Знайти раціональні корені рівняння

.

Затверджено на засіданні кафедри інформатики

18 травня 2011 року (протокол №10)

Завідувач кафедри ________________ Щирба В.С.