lab3
.docСанкт-Петербургский государственный электротехнический университет
«ЛЭТИ»
Кафедра ТОР
Отчет
по лабораторной работе № 3
Исследование функций распределения и плотностей вероятности значений случайных сигналов
Выполнили Пташкин А.А.
Петров А.
Скирдаченко И.
Эльксне Н.
Факультет РТ
Группа № 4122
Преподаватель
Санкт-Петербург
2006 г.
Цель работы — исследование одномерных функций распределения вероятностей и плотностей вероятностей значений случайных сигналов.
Описание лабораторной установки
Лабораторная установка состоит из отдельного макета и двух осциллографов С1–83 (I) и С1–83 (II).
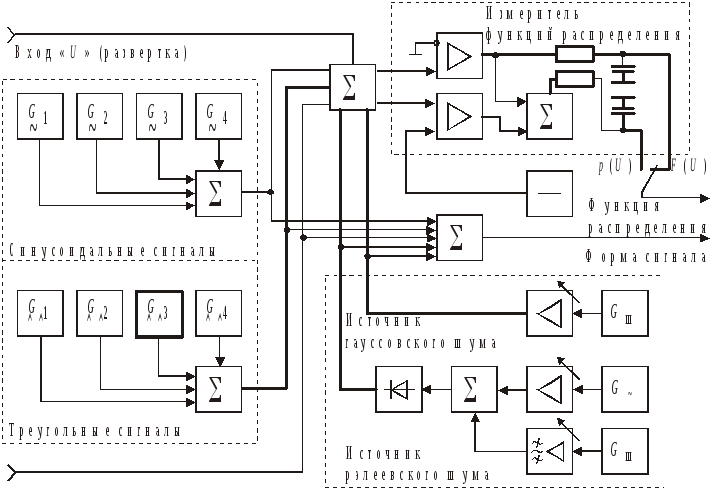
В отдельном макете находятся генератор исследуемых случайных сигналов, а также измерители функции распределения вероятностей и плотности распределения вероятностей. Структурная схема макета установки изображена на его передней панели.
С выхода «![]() »
осциллографа С1–83 (I) снимается в качестве
опорного пилообразное напряжение
горизонтальной развертки и подается в
лабораторный макет на «Вход U»
для использования в качестве аргумента
«U» функции распределения.
»
осциллографа С1–83 (I) снимается в качестве
опорного пилообразное напряжение
горизонтальной развертки и подается в
лабораторный макет на «Вход U»
для использования в качестве аргумента
«U» функции распределения.
Выход «Функция распределения» установки соединяется с входом «» осциллографа С1–83 (I). На экране осциллографа появляется изображение функции распределения F(U) или плотности распределения вероятностей p(U). Выбор зависит от положения переключателя «F(U) — p(U)» на передней панели экспериментальной установки.
Выход «Форма сигнала» установки соединяется со входом «» осциллографа С1–83 (II), на экране которого наблюдают изображение исследуемого сигнала.
В макете установки имеются следующие источники сигналов:
-
Четыре генератора гармонических колебаний различных частот.
-
Четыре генератора сигналов треугольной формы различных частот.
-
Формирователь шума с распределением по обобщенному закону Рэлея.
-
Генератор шума с гауссовским законом распределения.
Имеется также вход для внешнего сигнала.
Выходы всех источников сигналов подключены через сумматор ко входу измерителя функций распределения. Каждый источник сигнала имеет тумблер включения и регулировку уровня (только часть регуляторов уровня выведена на переднюю панель).
ОТЧЕТ.
-
Коэффициент развертки и коэффициент отклонения
Кр=0,1 с/дел
Ко=0,2 В/дел
-
Определение масштаба графиков
Изображение треугольного сигнала
U2-U1![]()



График функции распределения


L
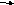

L=3,2 дел.
U2-U1=0,4 В
Масштаб = (U2-U1)/L = 0,125 В/дел
Таблица № 1
|
Сигнал |
Форма сигнала |
График функции распределения |
|
Треугольный Амплитуда 0,125 В
|
|
|
|
Треугольный Амплитуда 0,1875 В
|
|
|
|
Гармонический Амплитуда 0,125 В
|
|
|
|
Гармонический Амплитуда 0,1875 В
|
|
|
|
Гауссовский шум
|
|
|
|
Гауссовский шум
|
|
|
|
Рэлеевский шум Амплитуда 0,0 В
|
|
|
|
Рэлеевский шум Амплитуда ≠ 0,0 В
|
|
|
3. Графики функций распределения сигналов и анализ соответствия графиков теоретическим результатам
Треугольный сигнал
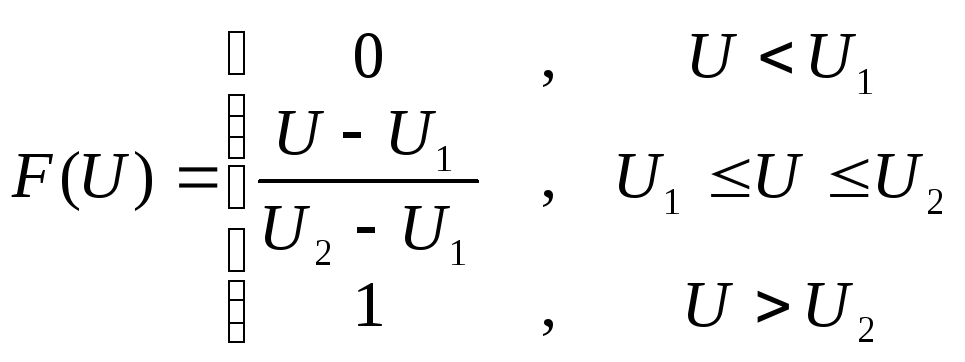 (1)
(1)
График функции распределения треугольного сигнала, полученный экспериментально, соответствует теоретической формуле (1).
Гауссовский шум
![]() (2)
(2)
График функции распределения гауссовского шума, полученный экспериментально, соответствует теоретической формуле (2).
Гармонический сигнал
![]() (3)
(3)
График функции распределения гармонического сигнала, полученный экспериментально, соответствует теоретической формуле (3).
-
Графики функций распределения для последовательных сумм синусоидальных треугольных сигналов
Последовательность сумм синусоидальных сигналов
Сигнал №1

Сигнал №1+ Сигнал №2

Сигнал №1+ Сигнал №2+ Сигнал №3

Сигнал №1+ Сигнал №2+ Сигнал №3+ Сигнал №4

Последовательность сумм треугольных сигналов
Сигнал №1
Сигнал №1+ Сигнал №2

Сигнал №1+ Сигнал №2+ Сигнал №3

Сигнал №1+ Сигнал №2+ Сигнал №3+ Сигнал №4

Вывод: Для треугольного сигнала
(равномерный закон распределения)
характерна более быстрая сходимость к
гауссовскому закону, чем для гармонического
сигнала (закон распределения вида
![]() ).
).