15. Бесконечно малые функции, сравнение бесконечно малых, теорема об эквивалентных бесконечно малых. Определение. Функция ℒ(x) называется бесконечно малой в точке а, если Справедливо утверждение: если функция f(х) имеет в точке а предельное значение равное b, то разность ℒ(х)=f(x) - b является бесконечно малой в точке a.

Доказательство. 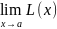= = - = b - b = 0 => ℒ(x) – бесконечно малая в точке a. Таким образом, если , то f(x) можно представить как f(x) = b + ℒ(x), где ℒ(х) – бесконечно малая в точке a.

Сравнение бесконечно малых

Пусть ℒ(x) и β(x) – бесконечно малые функции при x⟶a 1. Функция ℒ(x) называется бесконечно малой более высокого порядка относительно β(x), если = 0

Обозначение: ℒ(х) = ō(β(х)) (ō – «о малое»)

2.Функции ℒ(х) и β(х) называются бесконечно малыми одного порядка, если существует конечный предел

3.Функции ℒ(х) и β(х) называются эквивалентными бесконечно малыми, если предел

Обозначение: ℒ(х)~β(х)

4.Функция ℒ(х) называется бесконечно малой порядка m относительно β(х) если Ǝ(существует) конечный предел , где число m – порядок малости. Примеры: 1) Т.к. 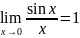, то sin x ~x (при х⟶0)

2) Т.к. = 1, то ln(1+x)~1 (при х⟶0)

3) Т.к. = 1, то e^x~1+x (при х⟶0)

. = a

(1+x)^a~1+ax

Теорема

Если ℒ(х) ~ℒ₁(х), β(х)~β₁(х) (при х⟶а) то =

Пример:

= =

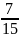
tg 7x~7x²; sin 5x~5x; ln(1+3x)~3x

16. Два определения непрерывности функции в точке, односторонняя непрерывность функции в точке, примеры.

Определение 1* Функция y = f(x) называется непрерывной в точке а, если она определена в этой точке и предельное значение функции f(x) в точке а равно частному значению f(a)

= f(a) (1)

Т.к. а = lim x, то х⟶а

Равенство (1) можно записать в виде = f ) (1^/)

Под знаком непрерывности функции можно переходить к пределу.

Определение 1 подразумевает выполнение 3х условий:

1. Функция f(x) должна быть определена в точке а, то есть существует конечное значение f(a)

2. Ǝ предельное значение f(x) в точке а, то есть Ǝ

3. Справедливо равенство: = f(a),

если хотя бы одно из условий 1-3 нарушено, то точка а – точка разрыва функции f(x)

Запишем равенство (1) в виде

Условие х⟶а эквивалентно условию х-а⟶0,

Поэтому

Обозначим ∆ x = x-a – приращение аргумента х функции f(x) в точке а f(x) – f(a) = ∆y – приращение функции y = f(x) в точке а, соответствующее приращению аргумента ∆x Можно записать, что x = a + ∆x ∆y = f(x) – f(a) = f(a + ∆x) – f(a)

Равенство 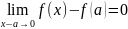принимает вид (2)

Определение 2 функция y=f(x) называется непрерывной в точке а, если она определена в некоторой окрестности точки а, а так же в самой точке а и бесконечно малому приращению аргумента в точке a соответствует бесконечно малое приращение функции

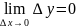(2)

Пример 1. Покажем, что многочлен P_n(x) является непрерывной функцией в точке а

P_n(x) = b₀ + b₁x + b₂x² + …+ b_nxⁿ – многочлен степени n (b₀, B₁, b₂…b_n), bⁿ ≠0 – коэффициент многочлена, т.к. , то по теореме о произведении пределов = = 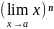aⁿ, тогда используя это равенство:

_n (x) = ₀ + ₁x +…+ _nxⁿ = ₀ + b₁a + b₂a² +…+ b_naⁿ = P_n(a)

Получим, что _n (x) существует и равен P_n(a). По определению (1) это значит, что многочлен P_n(х) непрерывен в точке а _n (x) = P_n (a)

Если рассмотреть рациональную дробь , где P_n (x) – многочлен степени n; Q_n (x) – многочлен степени m, то = ^{(теорема определения частного)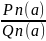} = , Q_n (a) ≠ 0

Рациональная дробь непрерывна в точке, где знаменатель ≠ 0

Пример 2. Покажем, что функция y=sin x непрерывна в любой точке x (по определению (2)).

│∆y│=│sin(x + ∆x) – sin x│=│2sin ( ) cos(x + )│≤ 2│sin │, т.к.│cos (x + )│ ≤ 1. При выводе первого замечательного предела показали, что sin x <x,

тогда │∆y│≤ 2│sin │< 2 │ = │∆x│, то есть │∆y│<│∆ x│, поэтому = 0 по определению (2) это означает непрерывность функции y = sin x.

Определение

Функция y = f(x) называется непрерывной в точке а справа (слева), если правое(левое) предельное значение этой функции в точке а существует и равно частному значению f(a)

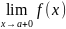= f(a) или f(a + 0) = f(a) – непрерывная справа

или f(a – 0) = f(a) – непрерывная слева

Утверждение: если функция f(x) непрерывна в точке а и справа и слева, то она непрерывна в этой точке. При этом = f(a) = =

Определение

Функция f(x) называется непрерывной на множестве x , если она непрерывна в каждой точке этого множества.

17. Арифметические операции над функциями, непрерывными в точке; непрерывность сложной функции. Доказательство теоремы об арифметических операциях над непрерывными функциями.

Теорема 1

Если заданные на одном множестве функции f(x) и g(x) непрерывны в точке а, то функции f(x)±g(x), f(x)·g(x), (g(x) ≠0) – непрерывны в точке а.

Доказательство

Т.к. f(x) и g(x) непрерывны в точке а, то по определению (1) непрерывности

= f(a), 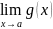= g(a).

По теореме об арифметических операциях над функциями, имеющими предел, будем иметь:

= ± = f(a)±g(a)

= f(a) · g(a)

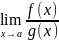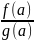= , g(a)≠0

Полученные равенства означают непрерывность функций f(x)±g(x), f(x)·g(x), в точке а. ч.т.д.

Пусть функция x = φ(t) определена для некоторого множества T и принимает значения на множестве Х, пусть далее на множестве Х определена функция y=f(x). Тогда на множестве Т задана сложная функция y = f(x), где х = φ(t) или y= f(φ(t)) = F(t).

Теорема 2

Если функция х = φ(t) непрерывна в точке а, а функция y = f(x) непрерывна в точке b, которая равна φ(а), то сложная функция y = f(φ(t)) = F(t) непрерывна в точке а.

Утверждение теоремы можно записать в виде формулы: f( .

Под знаком непрерывной функции можно переходить к пределу.

При вычислении пределов можно делать замену переменной, используя соотношение

= (φ(t)), где х = φ(t), b = φ(a)