3.2 Передаточная функция системы

Структурная схема следящей системы представлена на рисунке 8:

Рисунок 8 – Структурная схема некорректированной следящей системы

3.2.1 Передаточная функция разомкнутой системы:

Устанавливает связь между Y(p) и (р):

; (3.33)

где K_v = К_изм  К_фз  К_у  К_эму  К_дв  К_ред , откуда:

(3.34)

Таким образом, передаточная функция разомкнутой систему будет выглядеть следующим образом:

(3.35)

3.2.2 Передаточная функция замкнутой системы по задающему воздействию:

; (3.36)

где С(р)=с₅р⁵+с₄р⁴+с₃р³+с₂р²+с₁р+с₀; (3.37)

С помощью ЭВМ были вычислены коэффициенты:

с₅ = 0.00006407 с₂ = 0.412

с₄ =0.003255 с₁ = 1

с₃ =0.05758 с₀ = 141

Полученная передаточная функция замкнутой системы по задающему воздействию примет вид:

(3.38)

3.2.3 Передаточная функция системы по возмущающему воздействию

Устанавливает связь между У(р) и –М_с(р):

(3.39)

3.2.4 Передаточная функция ошибки по задающему воздействию

Устанавливает связь между _х(р) и Х(р):

; (3.40)

3.2.5 Передаточная функция ошибки по возмущающему воздействию

3.3 Определение и построение лачх и лфчх разомкнутой некорректированной системы

Передаточная функция разомкнутой системы имеет вид:

(3.41)

Логарифмическая амплитудно-частотная характеристика в соответствии с передаточной функцией разомкнутой системы имеет вид:

(3.42)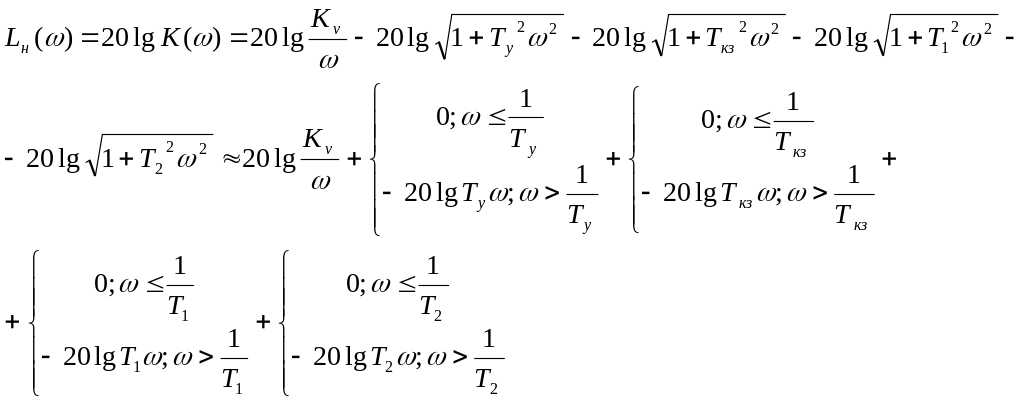

Для построения асимптотической ЛАЧХ достаточно определить

20lgK_v = 20lg 141 = 42,98 дБ и сопрягающие частоты: с^-1; с^-1;

с^-1; с^-1;

Логарифмическая фазочастотная характеристика определяется выражением:

(3.43)

3.4 Определение устойчивости замкнутой некорректированной системы

Для определения устойчивости замкнутой системы по известным параметрам разомкнутой системы существует масса критериев, но из всего многообразия способов, воспользуемся критерием определения устойчивости по корням характеристического уравнения и логарифмическим критерием устойчивости.

3.4.1 Определение устойчивости по корням характеристического уравнения заключается в определении знака вещественных частей корней характеристического уравнения замкнутой системы:

С(р) = С⁵р⁵ + С₄р⁴ + С₃р³ + С₂р² + С₁р + С₀ =0 (3.44)

Корни этого уравнения определим с помощью ЭВМ, и результат сведём в таблицу.

Таблица 5. Корни системы

Корни рi	Re pi	Im pi
р1	6.0088	10.0602
p2	-16.3267	16.2696
p3	-30.1678	0
p4	-16.3267	-16.2696
p5	6.0088	-10.0602

Т.к. корни р₁ и p₅ имеют положительную вещественную часть, то замкнутая система неустойчива.

3.4.2 Определение устойчивости по логарифмическому критерию сводится к определению значения ЛФХ на частоте среза и если значение ЛФХ меньше -180⁰, то делают вывод о том, что данная замкнутая система неустойчива. В нашем случае на частоте среза ЛФХ принимает значение , следовательно замкнутая система по логарифмическому критерию неустойчива.