
Глава 3.
ДАЛЬНЕЙШИЕ ТЕОРЕТИКО-МОДЕЛЬНЫЕ КОНСТРУКЦИИ
§3.1 Элементарные расширения
Говорят, что![]() –
элементарная
подмодель модели
(
–
элементарная
подмодель модели
(![]() ),
если
),
если ![]() и
для всякой
и
для всякой ![]() и
и ![]()
![]()
Тогда ![]() называют
элементарным расширением модели
.
называют
элементарным расширением модели
.
Пусть
Х
А
и ![]() .
Следующее предложение очевидно.
.
Следующее предложение очевидно.
10. ( +3.2 )ПРЕДЛОЖЕНИЕ 3.1
Если
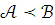 ,
то
,
то 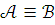 .
.Если и
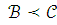 ,
то
,
то 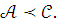
Если
 и
и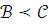 и
и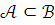 ,
то
.
,
то
.
ПРЕДЛОЖЕНИЕ 3.2.
![]() и для всякой формулы
и для всякой формулы ![]() и любых
,
если
и любых
,
если ![]() ,
то найдется
,
то найдется ![]() ,
что
,
что ![]() .
.
ДОКАЗАТЕЛЬСТВО. По сложности докажем для
![]()
Это очевидно для
атомных логических связок. Если должны
![]() и
и ![]() ,
то есть
,
то есть ![]() такой, что
такой, что ![]() .
По предположению индукции
.
По предположению индукции ![]() и поэтому
и поэтому ![]() .
Если же
,
то по условию есть
,
что
.
По предположению индукции
,
значит и
.
.
Если же
,
то по условию есть
,
что
.
По предположению индукции
,
значит и
.
Элементарным
вложением
в![]() называется
всякий изоморфизм
называется
всякий изоморфизм ![]() модели
на элементарную подмодель модели
модели
на элементарную подмодель модели ![]()
Пусть ![]() .
Элементарной
диаграммой модели
называется теория
.
Элементарной
диаграммой модели
называется теория![]() ,
состоящая из всех предложений языка
,
состоящая из всех предложений языка
![]() ,истинных
в модели
,истинных
в модели ![]() .
.
11.
ПРЕДЛОЖЕНИЕ
3.3. Пусть ![]() – элементарная диаграмма модели
.
– элементарная диаграмма модели
.
![]() некоторое обогащение
некоторое обогащение ![]() модели
служило моделью для
.
Если
модели
служило моделью для
.
Если ![]() ,
то
,
то ![]() .
.
ПРЕДЛОЖЕНИЕ 3.4.
Пусть ![]() - непустое множество элементарно
эквивалентных моделей. Тогда существует
модель
такая, что всякая
- непустое множество элементарно
эквивалентных моделей. Тогда существует
модель
такая, что всякая ![]() элементарно
вложима в
элементарно
вложима в![]()
ДОКАЗАТЕЛЬСТВО.
Для каждой ![]() пусть
ее элементарная диаграмма. Можно считать,
что
пусть
ее элементарная диаграмма. Можно считать,
что![]() .
Пусть
.
Пусть ![]() .
Утверждаем, что
.
Утверждаем, что ![]() – непротиворечивое множество. Пусть
– непротиворечивое множество. Пусть
![]() – конечное подмножество
.
Можно считать, что
– конечное подмножество
.
Можно считать, что ![]() принадлежат различным слагаемым
принадлежат различным слагаемым![]() множества
множества ![]() .
Тогда существуют
.
Тогда существуют ![]() от переменных
от переменных ![]() и элементы
и элементы ![]() ,
что
,
что ![]() и
и ![]() Поскольку
Поскольку ![]() при
при ![]() получаем, что предложение
получаем, что предложение
![]()
истинно в модели
![]() ,
т.е.
,
т.е. ![]() непротиворечиво. По теореме компактности
непротиворечиво. По теореме компактности
![]() имеет
модель
.
Пусть
- объединение
до модели исходного языка
.
По предложению 3.3
элементарно вложимо в
имеет
модель
.
Пусть
- объединение
до модели исходного языка
.
По предложению 3.3
элементарно вложимо в![]()
12. ТЕОРЕМА 3.5 (об элементарных расширениях вверх). Всякая бесконечная модель обладает сколь угодно большими элементарными расширениями.
ДОКАЗАТЕЛЬСТВО.
Пусть
– элементарная диаграмма ![]() По теореме Лёвенгейма-Скулема
По теореме Лёвенгейма-Скулема ![]() имеет
сколь угодно большие модели и осталось
сослаться на предложение 3.3.
имеет
сколь угодно большие модели и осталось
сослаться на предложение 3.3.
ТЕОРЕМА 3.6 (об
элементарных подмоделях вниз). Пусть
– модель мощности ![]() и
и ![]() .
Тогда
.
Тогда ![]() элементарную подмодель мощности
элементарную подмодель мощности ![]() .
Если же
.
Если же ![]() ,
то
имеет элементарную подмодель мощности
,
то
имеет элементарную подмодель мощности
![]() содержащую Х.
содержащую Х.
ДОКАЗАТЕЛЬСТВО.
Для всякой формулы ![]() и n-ки
и n-ки![]() ,
удовлетворяющих условию
,
удовлетворяющих условию ![]() выберем
выберем![]() такой, что
такой, что ![]() .
Считаем
.
Считаем ![]() получено из Х присоединением к нему
всех таких b.
Т.к.
получено из Х присоединением к нему
всех таких b.
Т.к. ![]() и
и ![]() ,
то
,
то ![]() .
Повторим этот процесс счетное число
раз, получая
.
Повторим этот процесс счетное число
раз, получая ![]() и положим
и положим![]() .
Множество В замкнуто относительно
функции
.
Пусть
подмодель
,
причем основное множество
.
Множество В замкнуто относительно
функции
.
Пусть
подмодель
,
причем основное множество ![]() есть В. Пусть
есть В. Пусть ![]() для
для ![]() .
Для некоторого m
.
Для некоторого m![]() .
Тогда найдется
.
Тогда найдется ![]() и по предложению 3.2 имеем
и по предложению 3.2 имеем ![]()
Теория Т называется
модельно
полной, если
для любых моделей
и
теории Т ![]() влечет
влечет ![]() .
.
13. ПРЕДЛОЖЕНИЕ 3.7 (критерий модельной полноты). Если Т – теория в языке , то следующие утверждения эквивалентны:
Теория Т – модельно полна
Для всякой модели
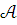 теории Т теория
теории Т теория 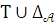 полна в языке
полна в языке 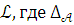 – диаграмма
– диаграмма 
Если
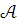 и
и
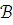 - модели Т и
,
то всякое
- модели Т и
,
то всякое  -предложение,
истинное в модели
-предложение,
истинное в модели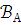 ,
истинно и в
,
истинно и в 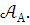
Для всякой формулы
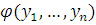 существует такая
существует такая 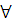 -формула
-формула
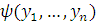 ,
что
,
что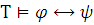 .
.
ДОКАЗАТЕЛЬСТВО.
(1)![]() (2)
Пусть
– модель Т. Т.к. любое расширение модели
(2)
Пусть
– модель Т. Т.к. любое расширение модели
![]() элементарно,
теория
элементарно,
теория ![]() имеет в точности те же модели, что и
элементарная диаграмма
имеет в точности те же модели, что и
элементарная диаграмма ![]() и поэтому
полна.
и поэтому
полна.
(2)
(3)
Если
и
- модели Т и
,
то и ![]() служат
моделями полной теории
,
т.к всякое
служат
моделями полной теории
,
т.к всякое ![]() -предложение,
истинное в
-предложение,
истинное в![]() ,
истинно и в
,
истинно и в ![]()
(3)
(4)
Пусть ![]() -формула,
– множество всех
-формула,
– множество всех ![]() -предложений
-предложений
![]() язака
язака ![]() ,
для которых
,
для которых ![]() .
Пусть
.
Пусть ![]() -
модель
-
модель ![]() ,
а
,
а ![]() – диаграмма модели
.
Всякая конечная конъюнкция
– диаграмма модели
.
Всякая конечная конъюнкция ![]() предложений теории
совместима с теорией
предложений теории
совместима с теорией ![]() ,
т.к.
-предложение
,
т.к.
-предложение
![]() ложно в
и поэтому не входит в Г и не является
следствием
.
Поэтому теория
ложно в
и поэтому не входит в Г и не является
следствием
.
Поэтому теория ![]() имеет модель
.
Значит
,
причем
- модель Т. В силу (3), всякое
-предложение,
истинное в модели
,
истинно и в
В частности
имеет модель
.
Значит
,
причем
- модель Т. В силу (3), всякое
-предложение,
истинное в модели
,
истинно и в
В частности ![]() истинна в модели
.
Заключаем: всякая модель
истинна в модели
.
Заключаем: всякая модель ![]() будет моделью и для
будет моделью и для ![]() ,
т.е.
,
т.е. ![]() .
По теореме компактности есть
.
По теореме компактности есть ![]() такие, что
такие, что ![]() .
Значит
.
Значит ![]() .
Вынося кванторы вперед и заменяя
константы
.
Вынося кванторы вперед и заменяя
константы ![]() переменными
переменными ![]() ,
получим
-формулу
для которой
,
получим
-формулу
для которой![]() ,
т.е. для всякой
такая
есть.
,
т.е. для всякой
такая
есть.
(3)
(4)
Пусть
и
- модели Т, ![]() и предположим, что
и предположим, что ![]() ,
а
-
-формула
для которой
,
а
-
-формула
для которой ![]() .
Тогда
.
Тогда ![]() и
.
Поэтому
и теория Т модельно полна.
и
.
Поэтому
и теория Т модельно полна.
СЛЕДСТВИЕ 3.8. Пусть
теория Т не имеет конечных моделей и
![]() .
Тогда следующие утверждения являются
необходимыми и достаточными условиями
модельной полноты Т:
.
Тогда следующие утверждения являются
необходимыми и достаточными условиями
модельной полноты Т:
Для всякой модели теории Т, для которой
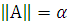 теория
полна.
теория
полна.Если и - модели Т, для которых
 и
,
то всякое
- предложение, истинное в
,
истинно и в
и
,
то всякое
- предложение, истинное в
,
истинно и в 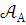 .
.
14. ПРЕДЛОЖЕНИЕ 3.9 (о связи полноты и модельной полноты). Пусть теория Т модельно полна. Тогда
Если любые две модели Т изоморфно вкладываются в третью модель Т, то теория полна.
Если Т обладает моделью, изоморфно вкладывающейся в любую модель Т, то теория Т полна.
ДОКАЗАТЕЛЬСТВО. Вытекает из того факта, что изоморфное вложение одной модели Т в другую модель Т является элементарным вложением.
15.
ПРЕДЛОЖЕНИЕ
3.10 (Тесть Лося-Вота).
Всякая непротиворечивая теория Т имеющая
лишь бесконечные модели и -категоричная
в некоторой мощности ![]() является полной.
является полной.
ДОКАЗАТЕЛЬСТВО.
Достаточно показать, что любые две
модели
и
теории Т эквивалентны. По теореме
Лёвенгема-Скулема, существуют такие
модели ![]() и
мощности
,
что
и
мощности
,
что ![]() и
и ![]() .
Но в силу
-категоричности
теории Т,
.
Но в силу
-категоричности
теории Т, ![]() ,
а поэтому
,
а поэтому![]() и
.
и
.
В силу этого предположения следующие теории, категоричные в некоторых бесконечных мощностях, оказываются полными.
Теория плотно линейно упорядоченных множеств без конечных точек (
 -категоричная)
-категоричная)Теория безатомных булевых алгебр ( -категоричная)
Теория алгебраически замкнутых полей (
 -категоричная)
-категоричная)Теория бесконечных абелевых групп экспоненты р
Теория перестановки множества А без конечных циклов ( -категорична)
Цепью
моделей называется
возрастающая последовательность
моделей ![]() упорядоченная по типу ординала
упорядоченная по типу ординала![]() Объединением
такой цепи есть модель
Объединением
такой цепи есть модель ![]() .
Ее основное множество будет
.
Ее основное множество будет![]() ,
а каждое отношение R
(функция G)
есть объединение
,
а каждое отношение R
(функция G)
есть объединение ![]()
16. ТЕОРЕМА 3.11 (Линдстрём) Пусть Т – теория в счетном языке со свойствами
Все модели теории Т бесконечны.
Объединение всякой цепи моделей Т будут моделью теории Т.
Т –
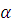 – категорична для некоторого кардинала
– категорична для некоторого кардинала

Тогда теория Т модельно полна.
ДОКАЗАТЕЛЬСТВО:
Модель
назовем Т-расширением модели
,
если
и ![]() - модели Т. Модель
теории Т называется алгебраически
замкнутой, если для любого расширения
модели
,
всякое
-предложение,
истинное в
,
истинно и в
- модели Т. Модель
теории Т называется алгебраически
замкнутой, если для любого расширения
модели
,
всякое
-предложение,
истинное в
,
истинно и в![]() .
Согласно предложению 3.7 и следствию 3.8
теория Т модельно полна тогда и только
тогда, когда всякая ее модель мощности
алгебраически замкнута.
.
Согласно предложению 3.7 и следствию 3.8
теория Т модельно полна тогда и только
тогда, когда всякая ее модель мощности
алгебраически замкнута.
Пусть
-
модель Т мощности
и ![]() – множество всех
-предложений
языка
.
Образуем цепь моделей Т
– множество всех
-предложений
языка
.
Образуем цепь моделей Т ![]() имеющих мощность
и если предложение
имеющих мощность
и если предложение ![]() истинно в некотором Т-расширении
истинно в некотором Т-расширении ![]() ,
то оно истинно и в
,
то оно истинно и в ![]() .
Положим
.
Положим ![]() ,
тогда всякое
-предложение
,
истинное в некотором Т-расширении модели
,
тогда всякое
-предложение
,
истинное в некотором Т-расширении модели
![]() истинно и в
истинно и в ![]() Повторяя это построение
раз получим цепь
Повторяя это построение
раз получим цепь ![]() ,
в которой всякое
-предложение
истинное в некотором Т-расширении модели
,
в которой всякое
-предложение
истинное в некотором Т-расширении модели
![]() ,
истинно в
.
Отсюда следует, что объединение этой
цепи
,
истинно в
.
Отсюда следует, что объединение этой
цепи ![]() – алгебраически замкнутая модель теории
Т мощности
– алгебраически замкнутая модель теории
Т мощности ![]() Теперь,
воспользовавшись
-категоричностью
Т, получаем, что всякая ее модель мощности
алгебраически замкнута. Но Т не имеет
конечных моделей и по следствию 3.8 теория
Т модельно полна.
Теперь,
воспользовавшись
-категоричностью
Т, получаем, что всякая ее модель мощности
алгебраически замкнута. Но Т не имеет
конечных моделей и по следствию 3.8 теория
Т модельно полна.
17.
ТЕОРЕМА 3.12 (Об элементарных цепях).
Пусть ![]() - элементарная цепь моделей,
- элементарная цепь моделей, ![]() Тогда
Тогда ![]() .
Индукцией по формуле
докажем: для всякой
.
Индукцией по формуле
докажем: для всякой ![]() ,
всякого ординала
,
всякого ординала ![]() и любых
и любых ![]()
![]()
Для атомных формул
и введения логических связок шаг индукции
осуществляется легко. Пусть теперь ![]() и
и ![]() Если
Если
![]() ,
то существует
,
то существует ![]() такой, что
такой, что ![]() .
По предположению индукции
.
По предположению индукции ![]() и
.
Тогда для некоторых
и
.
Тогда для некоторых ![]() и
имеем
и
имеем ![]() и
.
Т.к.
и
.
Т.к. ![]() образуют
цепь, можно считать, что
образуют
цепь, можно считать, что ![]() Но
и по индукции
Но
и по индукции ![]() и поэтому
и поэтому ![]() .
Но т.к.
.
Но т.к. ![]() окончательно
получаем
окончательно
получаем ![]() .
.
СЛЕДСТВИЕ 3.13 Объединение цепи моделей модельно полной теории Т сама является моделью Т.
ТЕОРЕМА 3.13 (об
элементарных цепях). Пусть ![]() -
элементарная цепь моделей. Тогда
при любом
.
-
элементарная цепь моделей. Тогда
при любом
.
ДОКАЗАТЕЛЬСТВО:
Положим ![]() и индукцией по формуле
докажем: для каждой формулы
,
ординала
и любых
,
и индукцией по формуле
докажем: для каждой формулы
,
ординала
и любых
,
![]()
Для атомных формул
это очевидно, как и при введении
пропозициональных связок. Пусть теперь
![]() и
и
![]() .
Если
.
Если ![]() ,
то существует
такой, что
,
то существует
такой, что ![]() .
По предположению индукции
и
.
По предположению индукции
и ![]() Если же
Если же ![]() ,
то для некоторых
и
имеем
и
.
Т.к.
образуют
цепь, можно считать, что
,
то для некоторых
и
имеем
и
.
Т.к.
образуют
цепь, можно считать, что ![]() Но
и по предположению индукции
и поэтому
.
Но
получаем
.
Но
и по предположению индукции
и поэтому
.
Но
получаем
.
СЛЕДСТВИЕ 3.14 Объединение всякой цепи моделей модельно полной теории Т само является моделью Т.
ДОКАЗАТЕЛЬСТВО:
Приведем пример, показывающий, что ![]() нельзя заменить
нельзя заменить ![]() .
Пусть
.
Пусть ![]() .
Добавляя n
элементов в начале
,
получим
.
Добавляя n
элементов в начале
,
получим ![]() причем
причем ![]() ,
но
,
но ![]() не имеет первого элемента. Значит
не имеет первого элемента. Значит ![]() .
.
18. Дадим прямое доказательство теоремы Робинсона без использования интерполяционной теоремы Крэйга.
(ТЕОРЕМА
(Робинсона о непротиворечивости) пусть
![]() и
и
![]() языки и
языки и
![]() .
Если Т полная теория в языке
.
Если Т полная теория в языке
![]() ,
а
,
а
![]() и
и
![]() –
непротиворечивые теории в языках
и
,
то
–
непротиворечивые теории в языках
и
,
то
![]() –непротиворечивая
теория в языке
–непротиворечивая
теория в языке
![]() .)
.)
Пусть ![]() и
– моделFи
теорий
и
– моделFи
теорий ![]() и
и ![]() .
Условимся, что
.
Условимся, что ![]() означает элементарную эквивалентность
- объединений моделей
и
,
означает элементарную эквивалентность
- объединений моделей
и
,
![]() - элементарное вложение
- элементарное вложение ![]() в
в ![]() ,
где
ограничение модели
по языку
.
Поскольку
,
где
ограничение модели
по языку
.
Поскольку ![]() и
и ![]() - модели полной теории Т, значит
- модели полной теории Т, значит ![]() .
Значит элементарная диаграмма модели
.
Значит элементарная диаграмма модели
![]() совместима
с элементарной диаграммой
совместима
с элементарной диаграммой ![]() Поэтому существует некоторое элементарное
расширение
Поэтому существует некоторое элементарное
расширение ![]() и вложение
и вложение ![]() .
Переходя к обобщенному языку
.
Переходя к обобщенному языку ![]() получаем
получаем ![]() .
Проводя такое же построение в другом
направлении, получим
.
Проводя такое же построение в другом
направлении, получим ![]() и вложение
и вложение
![]()
При
этом ![]() – продолжение
– продолжение ![]() .
Итерируя эти построения, получим
диаграмму,
.
Итерируя эти построения, получим
диаграмму,
![]()
![]()
![]()
![]()
![]()
в которой при
всяком
![]()
![]() и
и ![]() .
Положим
.
Положим ![]() ,
,
![]() Тогда
– модель теории
,
а
Тогда
– модель теории
,
а![]() – модель теории
– модель теории ![]() .
При этом отображении
.
При этом отображении ![]() будет изоморфизмом
на модель
.
Поэтому модель
изоморфна некоторой модели
будет изоморфизмом
на модель
.
Поэтому модель
изоморфна некоторой модели![]() ,
для
,
для ![]() .
Соединяя
и
в одно целое, получим такую модель
.
Соединяя
и
в одно целое, получим такую модель ![]() языка
языка ![]() ,
что
,
что ![]() .
Следовательно,
– модель теории
.
Следовательно,
– модель теории ![]() .
.
Формула
языка
называется ![]() – формулой, если она не содержит
кванторов.
– формулой, если она не содержит
кванторов. ![]() – формулой (
– формулой (![]() – формулой) будет формула
языка
,
имеющая вид
– формулой) будет формула
языка
,
имеющая вид ![]() (соответственно
(соответственно ![]() ),
где
есть
),
где
есть ![]() – формула (
– формула (![]() – формула). Аналогично определяются
– предложения (
– предложения). В частности экзистенциальные
(универсальные) предложения это
– формула). Аналогично определяются
– предложения (
– предложения). В частности экзистенциальные
(универсальные) предложения это ![]() – предложения (
– предложения (![]() – предложения).
– предложения).
Модель
называется
– расширением модели
,
если для всякой
– формулы ![]() и любых
и любых ![]() из
из ![]() следует
следует ![]() .
Цепь моделей
.
Цепь моделей ![]() называется
– цепью, если для любых
называется
– цепью, если для любых ![]() модель
модель ![]() является
– расширением модели
является
– расширением модели ![]() .
Всякое расширение модели будет ее
– расширением. Следующая лемма – аналог
теоремы 3.13.
.
Всякое расширение модели будет ее
– расширением. Следующая лемма – аналог
теоремы 3.13.
19. ЛЕММА 3.15. Пусть , – некоторая – цепь моделей и . Тогда
(а) Модель
является
– расширением каждой модели ![]()
(б) Всякое
– предложение, истинное во всех моделях
![]() истинно и в
истинно и в
ДОКАЗАТЕЛЬСТВО
(индукцией по n).
Для n=0
он верен. Предполагая, что он справедлив
для n=1,
докажем его для n.
Пусть ![]() – некоторая
– формула,
-
– некоторая
– формула,
- ![]() – формула. Предположим, что
– формула. Предположим, что ![]() на элементах
на элементах ![]() .
Тогда для некоторых
.
Тогда для некоторых ![]() имеем
имеем ![]() .
Пусть
.
Пусть ![]() .
Рассмотрим
– цепь
.
Рассмотрим
– цепь ![]() объединение
которой есть
объединение
которой есть ![]() .
Значит
.
Значит ![]() .
Этим доказано, что
-
– расширение модели
.
Этим доказано, что
-
– расширение модели
Для доказательства
(б) рассмотрим
–предложение ![]() ,
где
,
где ![]() -
– формула, истинное во всех
Пусть
.
Тогда
-
– формула, истинное во всех
Пусть
.
Тогда ![]() для некоторого
для некоторого ![]()
![]() на этих элементах, а потому и
на этих элементах, а потому и ![]() .
Значит
.
Значит ![]() .
.
Следующая теорема содержит доказательство одного утверждения о логике предикатов.
20. ТЕОРЕМА 3.16 (о – предложениях). Следующие утверждения эквивалентны (n>0):
Предложение
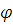 эквивалентно как некоторому
эквивалентно как некоторому 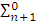 – предложению, так и некоторому
– предложению, так и некоторому 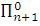 – предложению.
– предложению.Предложение эквивалентно некоторой булевой комбинации
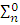 – предложений.
– предложений.
ДОКАЗАТЕЛЬСТВО.
Булева комбинация предложений это
всякая формула, полученная из них в
результате соединения произвольным
числом связок ![]() .
То, что булева комбинация
.
То, что булева комбинация ![]() предложений
эквивалентна
предложений
эквивалентна ![]() и
– предложению следует из того факта,
что к любому предложению можно добавить
фиктивные кванторы, не меняя его смысла.
и
– предложению следует из того факта,
что к любому предложению можно добавить
фиктивные кванторы, не меняя его смысла.
Обратно,
предположим, что выполняется (а). Сначала
докажем, что для любых моделей ![]()
Если всякое предложение истинно в
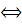 оно истинно в
,
то
оно истинно в
,
то 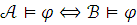 .
.
Пусть для моделей
![]() выполнена посылка (1). Построим
выполнена посылка (1). Построим ![]() цепь
моделей
цепь
моделей ![]() для
которой
для
которой
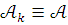 и
и 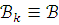 при любом
при любом 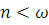 .
Пусть построена конечная
.
Пусть построена конечная 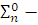 цепь
цепь
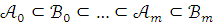 так, что (2) верно для всех
так, что (2) верно для всех  ,
а T
– совокупность всех
предложений
языка
,
а T
– совокупность всех
предложений
языка  ,
истинных в
,
истинных в 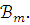 Ясно, что если дано конечное подмножество
множества T,
то, взяв конъюнкцию его предложений и
навесив квантор существование на все
новые константы, получим
предложение
Ясно, что если дано конечное подмножество
множества T,
то, взяв конъюнкцию его предложений и
навесив квантор существование на все
новые константы, получим
предложение
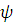 языка
языка 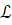 истинное в
По посылке (1)
истинное в
По посылке (1) 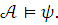 Итак, теория
Итак, теория 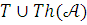 непротиворечива и поэтому имеет модель
непротиворечива и поэтому имеет модель
 .
Тогда цепь
.
Тогда цепь 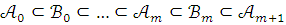 будет
цепью.
Применяя к
аналогичные рассуждения, получаем в
рассматриваемой
цепи
модель
будет
цепью.
Применяя к
аналогичные рассуждения, получаем в
рассматриваемой
цепи
модель 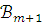 .
Если
.
Если 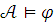 ,
то
,
то 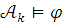 при любом k.
Но
является
при любом k.
Но
является 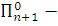 предложением и по лемме 3.15
истинно в модели
предложением и по лемме 3.15
истинно в модели 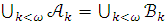 .
Если же
ложна в
,
то
.
Если же
ложна в
,
то 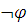 эквивалентно
предложению,
истинному в модели
эквивалентно
предложению,
истинному в модели 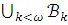 – противоречие.
– противоречие.
Установив
(1) рассуждаем так: если (б) ложно, то для
любой конечной совокупности
предложений,
скажем ![]() можно
указать такие модели
,
что
можно
указать такие модели
,
что
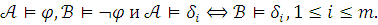 Это доказывается так: построим 2m
конъюнкций
Это доказывается так: построим 2m
конъюнкций
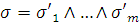 , где каждое
, где каждое 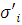 есть
есть
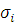 или
или
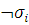 .
Некоторая конъюнкция
.
Некоторая конъюнкция 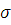 должна
быть совместима как с предложением
должна
быть совместима как с предложением 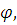 так и с
,
поскольку иначе имели бы
так и с
,
поскольку иначе имели бы 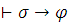 или
или 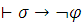 для всех таких
и
можно заключить, что
эквивалентно некоторой конечной
дизъюнкции таких предложений
и
(б) оказалось бы верным. Отправляясь от
(3) по теореме компактности получаем
модели
,
эквивалентные относительно всех
предложений,
но не эквивалентные относительно
,
что противоречит (1).
для всех таких
и
можно заключить, что
эквивалентно некоторой конечной
дизъюнкции таких предложений
и
(б) оказалось бы верным. Отправляясь от
(3) по теореме компактности получаем
модели
,
эквивалентные относительно всех
предложений,
но не эквивалентные относительно
,
что противоречит (1). 
Теорема верна и при n=0, если только язык содержит символы констант.
