
§ 2.3 Счётные модели полных теорий.
Если ![]() – полная теория, то формулу
– полная теория, то формулу ![]() называют полной
в теории
называют полной
в теории ![]() если для любой
если для любой ![]() имеет место в точности одно из соотношений
имеет место в точности одно из соотношений
![]() или
или ![]() .
.
Формула ![]() называется пополнимой
в теории
,
если для некоторой полной формулы
называется пополнимой
в теории
,
если для некоторой полной формулы ![]() .
Теория
называется атомной,
если всякая
совместимая с
формула пополнима в
.
Модель
.
Теория
называется атомной,
если всякая
совместимая с
формула пополнима в
.
Модель ![]() называется атомной,
если для всякой
n-ки
называется атомной,
если для всякой
n-ки
![]() существует полная в теории
существует полная в теории ![]() формула, выполняющаяся на этой n-ки.
формула, выполняющаяся на этой n-ки.
Пример. Пусть
- полная теория и ![]() - константы. Тогда формула
- константы. Тогда формула ![]() полна в
.
Если же
модель
такая, что всякий её элемент константа,
то
- атомная модель.
полна в
.
Если же
модель
такая, что всякий её элемент константа,
то
- атомная модель.
Пример. Всякая конечная модель и стандартная модель теории чисел атомная.
Пример. Следующая
теория
полна, но не имеет ни пополнимых формул,
ни атомных моделей. Её язык ![]() имеет предикатные символы
имеет предикатные символы ![]() , а аксиомы теории
таковы:
, а аксиомы теории
таковы: ![]() ,
где
,
где ![]() все различны.
все различны.
0.
ТЕОРЕМА (о существовании атомных
моделей). Пусть
- полная теория. Она имеет счетную атомную
модель ![]() - атомная теория.
- атомная теория.
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() имеет
атомную модель
,
совместима с
.
Имеем
имеет
атомную модель
,
совместима с
.
Имеем
![]()
Если
выполняется на n-к
![]()
![]() ,
- полная формула, выполняющаяся на этой
n-ке
, то
,
- полная формула, выполняющаяся на этой
n-ке
, то ![]() невозможна. Значит
невозможна. Значит ![]() ,
т.е. формула
пополняема, а теория
атомна.
,
т.е. формула
пополняема, а теория
атомна.
Обратно, пусть
– атомная теория. Для каждого ![]() обозначим через
обозначим через ![]() множество отрицаний всех полных формул
множество отрицаний всех полных формул
![]() .
Всякая совместимая с
формула
пополнима, а поэтому
.
Всякая совместимая с
формула
пополнима, а поэтому ![]() совместима с
при некоторой
совместима с
при некоторой ![]() .
Значит
локально опускает каждое множество
. По обобщенной теореме об опускании
типов
имеет счётную модель
,
опускающую каждое
.
Значит
локально опускает каждое множество
. По обобщенной теореме об опускании
типов
имеет счётную модель
,
опускающую каждое ![]() .
Поэтому для всякой n-ки
существует полная формула, выполняющаяся
на ней, т.е.
- атомная модель.
.
Поэтому для всякой n-ки
существует полная формула, выполняющаяся
на ней, т.е.
- атомная модель.
1.
ТЕОРЕМА (единственности для атомных
мод.) Если
и ![]() счётные
атомные модели и
счётные
атомные модели и ![]() ,
то
,
то![]() .
.
ДОКАЗАТЕЛЬСТВО.
Если
или
– конечная модель, то очевидно ![]() .
Пусть
и
бесконечны. Упорядочим А и В по типу
.
Пусть
и
бесконечны. Упорядочим А и В по типу
![]() .
Доказательство будет примером челночной
конструкции.
.
Доказательство будет примером челночной
конструкции.
Пусть ![]() - первый элемент А, а
- первый элемент А, а ![]() – некоторая полная формула, выполняющаяся
в
на элементе
.
Т.к.
– некоторая полная формула, выполняющаяся
в
на элементе
.
Т.к. ![]() ,
то и
,
то и ![]() .
Пусть теперь
.
Пусть теперь ![]() – первый элемент
– первый элемент ![]() ,
а
,
а ![]() - некоторая полная формула, выполняющаяся
в
на элементах
- некоторая полная формула, выполняющаяся
в
на элементах ![]() .
В силу полноты формулы
.
В силу полноты формулы ![]() ,
формула
,
формула
![]()
выполняется и в
и в
.
Поэтому есть такой ![]() ,
что
выполняется на паре
,
что
выполняется на паре ![]() .
Пусть теперь
.
Пусть теперь ![]() - первый элемент множества
- первый элемент множества ![]() и т.д. Перемещаясь
раз взад и вперед, получим
и т.д. Перемещаясь
раз взад и вперед, получим
![]() и
и ![]()
По ходу этих
перемещений будут исчерпаны множества
А и В, т.е. ![]() и
и ![]() .
К тому же, для всякого
.
К тому же, для всякого ![]() ,
на n-ках
,
на n-ках
![]() и
и ![]() выполняется одна и та же полная формула,
значит отображение
выполняется одна и та же полная формула,
значит отображение ![]() - изоморфизм
на модель
.
- изоморфизм
на модель
.![]()
Третий
результат об атомных моделях показывает,
что их следует мыслить, как ![]() модели тории
модели тории ![]() .
.
Отображение ![]() называется элементарным
вложением
модели
в
(символически
называется элементарным
вложением
модели
в
(символически ![]() ), если для всех формул
и n-ок
верно
), если для всех формул
и n-ок
верно
![]() .
.
Таким образом, элементарное вложение есть изоморфизм на элементарную подмодель модели .
Модель называется простой, если элементарно вкладывается во всякую модель теории , и счетно-простой, если - счетная модель элементарно вкладывающуюся во всякую счетную модель теории .
2. ТЕОРЕМА (об атомных моделях). Следующие утверждения эквивалентны:
(а) ![]() - счетная атомная модель;
- счетная атомная модель;
(б) - простая модель;
(в) – счетно-простая модель.
ДОКАЗАТЕЛЬСТВО.
Пусть
- счетная атомная модель, ![]() ,
,
![]() и
- модель
и
- модель![]() .
Если
.
Если ![]() - полная формула, выполняющаяся на
элементе
- полная формула, выполняющаяся на
элементе ![]() ,
то
,
то ![]() и поэтому есть
и поэтому есть ![]() такой, что
такой, что ![]() .
Если теперь
.
Если теперь ![]() – полная формула, выполняющаяся на паре
– полная формула, выполняющаяся на паре
![]() ,
то
,
то ![]() . Выбираем
такой, что
. Выбираем
такой, что ![]() и т.д. Отображение
будет элементарным вложение
в
.
и т.д. Отображение
будет элементарным вложение
в
.
Пусть теперь - простая модель. Тогда элементарно вложима во всякую счетную модель теории , а значит - счетно-простая модель.
Предположим, что
- счетно-проста,
и ![]() - множество всех формул
- множество всех формул ![]() ,
выполняющихся на
.
Для любой счетной модели
теории
существует
и поэтому множество
выполняется в
на элементах
,
выполняющихся на
.
Для любой счетной модели
теории
существует
и поэтому множество
выполняется в
на элементах ![]() .
Итак, Г реализуется во всякой счетной
модели
.
По теореме об опускании типов Г локально
реализуется
.
Поэтому существует совместимая с
формула
такая, что
.
Итак, Г реализуется во всякой счетной
модели
.
По теореме об опускании типов Г локально
реализуется
.
Поэтому существует совместимая с
формула
такая, что ![]() для всех
для всех ![]() .
Но для всякой
либо
.
Но для всякой
либо ![]() ,
либо
,
либо ![]() .
Поэтому
.
Поэтому![]() полна в теории
.
Невозможно
полна в теории
.
Невозможно ![]() и поэтому
и поэтому ![]() ,
т.е.
– полная формула и
,
т.е.
– полная формула и ![]() ,
т.е.
- атомная модель.
,
т.е.
- атомная модель.
Пусть дана модель
и ![]() .
Модель
.
Модель ![]() ,
,
![]() обозначаем через
обозначаем через ![]() ,
а соответствующий ей язык через
,
а соответствующий ей язык через ![]() .
Модель
называется -насыщенной,
если для всякого конечного
.
Модель
называется -насыщенной,
если для всякого конечного ![]() ,
любое совместное с теорией
,
любое совместное с теорией ![]() множество формул Г(х) языка
реализуется в
,
и счетно-насыщенной,
если
является счетной и
множество формул Г(х) языка
реализуется в
,
и счетно-насыщенной,
если
является счетной и ![]() – насыщенной. Заметим, что если
-
-насыщенная,
то и
тоже для любого конечного
.
– насыщенной. Заметим, что если
-
-насыщенная,
то и
тоже для любого конечного
.
ПРИМЕР. Всякая конечная модель; счетная модель теории равенства и упорядочение рациональных чисел счетно-насыщенной модели.
Вспомним, что тип
от переменных ![]() - это любое максимальное непротиворечивое
множество формул
.
Множество
- это любое максимальное непротиворечивое
множество формул
.
Множество ![]() всех предложений Г будет максимальной
непротиворечивой теорией, называемой
теорией типа Г, а если
всех предложений Г будет максимальной
непротиворечивой теорией, называемой
теорией типа Г, а если ![]() ,
то Г – тип теории
.
Для модели
в теории
и n-ки
множество всех формул
выполняющихся на
.
,
то Г – тип теории
.
Для модели
в теории
и n-ки
множество всех формул
выполняющихся на
.
Если ![]() - множество формул языка
,
то формулу
назовем следствием
- множество формул языка
,
то формулу
назовем следствием
![]() ,
если для любой модели
на всякой n-ки
,
если
,
если для любой модели
на всякой n-ки
,
если
![]()
Через ![]() обозначим множество всех следствий в
языке
обозначим множество всех следствий в
языке ![]() из множества предложений
из множества предложений ![]() .
Пусть
.
Пусть ![]() .
Между типами
языка
и
.
Между типами
языка
и ![]() языка
языка ![]() имеется взаимно однозначное соответствие.
Именно,
имеется взаимно однозначное соответствие.
Именно, ![]() ,
будет типом в языке
.
Обратно, если
- тип в языке
,
то множество формул
,
будет типом в языке
.
Обратно, если
- тип в языке
,
то множество формул
![]()
является единственным
типом
,
для которого ![]() =Г.
В определении -насыщенной модели
использовано множество формул от одной
свободной переменной, но использование
формул от любого конечного множества
переменных не приводит к усилению
вводимого понятия.
=Г.
В определении -насыщенной модели
использовано множество формул от одной
свободной переменной, но использование
формул от любого конечного множества
переменных не приводит к усилению
вводимого понятия.
3.
ПРЕДЛОЖЕНИЕ ![]() Если модель
-насыщенная, то для любого конечного
,
всякое совместное с теорией
множество
формул языка
реализуется в модели
Если модель
-насыщенная, то для любого конечного
,
всякое совместное с теорией
множество
формул языка
реализуется в модели![]() .
.
ДОКАЗАТЕЛЬСТВО
(индукцией по n).
Предположим, что результат справедлив
для n-1
и множество ![]() .
Совместимо с
.
Считаем, что Г замкнуто относительно
конечных конъюнкций и
.
Совместимо с
.
Считаем, что Г замкнуто относительно
конечных конъюнкций и
![]()
![]() совместимо с
и в силу предположения индукции найдётся
n-1-ка
совместимо с
и в силу предположения индукции найдётся
n-1-ка
![]() на которой
выполнимо в
на которой
выполнимо в ![]() Полагая
Полагая ![]() получим множество формул
получим множество формул ![]() совместимое с
совместимое с ![]() ,
т.к. для всех
,
т.к. для всех ![]() имеем
имеем ![]() .
В силу
- насыщенности
,
существует
.
В силу
- насыщенности
,
существует ![]() ,
на котором
,
на котором
* (
-насыщенные
модели от ![]()
![]() реализуется в модели
Но тогда
реализуют множество формул
реализуется в модели
Но тогда
реализуют множество формул ![]() в модели
в модели ![]() .
.
4.
ТЕОРЕМА (о существовании счетно-насыщенных
моделей). Если
Т -полная теория, то она имеет
счетно-насыщенную модель ![]() для всякого
в этой теории существует не более
счётного множества различных типов от
n
переменных.
для всякого
в этой теории существует не более
счётного множества различных типов от
n
переменных.
ДОКАЗАТЕЛЬСТВО. Пусть имеет счётно-насыщенную модель . По предыдущему предложению всякий тип T от n переменных реализуется в модели . Но никакая n-ка не может реализовывать два различных типа от n переменных. Поэтому T имеет не более чем счетное множество различных типов.
Предположим, что
теория T
имеет при всяком n
лишь счётное множество типов от n
переменных. Пусть язык ![]() ,
где
,
где ![]() - счётное множество констант. Для всякого
конечного
- счётное множество констант. Для всякого
конечного ![]() типы
типы ![]() теории T
в языке
теории T
в языке ![]() находятся во взаимно однозначном
соответствии с типами
находятся во взаимно однозначном
соответствии с типами ![]() теории T
языка
.
Поэтому T
и в языке
имеет счётное множество типов
и конечных множеств
теории T
языка
.
Поэтому T
и в языке
имеет счётное множество типов
и конечных множеств ![]() лишь счётное множество. Пусть теперь
лишь счётное множество. Пусть теперь
![]() список
всех типов T
во всех обогащениях
,
для конечных
и
список
всех типов T
во всех обогащениях
,
для конечных
и ![]() список
всех предложений языка
список
всех предложений языка ![]() Построим в языке
такую возрастающую последовательность
теорий,
Построим в языке
такую возрастающую последовательность
теорий, ![]() .
Что для всякого
.
Что для всякого ![]() .
.
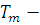 непротиворечивая
теория, содержащая лишь конечное число
констант из
непротиворечивая
теория, содержащая лишь конечное число
констант из 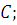
либо
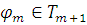 ,
либо ¬
;
,
либо ¬
;Если
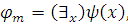 попадает
в
попадает
в 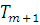 ,
то и
,
то и 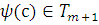 для некоторого
для некоторого 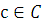 ;
;Если множество формул
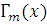 совместимо с
то
совместимо с
то 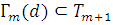 для некоторого
для некоторого 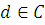 .
.
Теории ![]() строятся непосредственно, а
строятся непосредственно, а ![]() будет максимальной непротиворечивой
теорией в языке
.
Из условия (3)
будет максимальной непротиворечивой
теорией в языке
.
Из условия (3) ![]() имеет
такую модель
имеет
такую модель ![]() ,
что
,
что ![]() ,
т.е.
,
т.е. ![]() счётная
модель
.
счётная
модель
.
Осталось доказать
![]() насыщенность
модели
.
Пусть
конечно, а множества формул
насыщенность
модели
.
Пусть
конечно, а множества формул ![]() совместно с
.
Расширим
до некоторого типа
теории
.
Для подходящего
совместно с
.
Расширим
до некоторого типа
теории
.
Для подходящего ![]() имеем
имеем ![]() и
и ![]() совместим с теории
,
а поэтому и с теорией
совместим с теории
,
а поэтому и с теорией ![]() .
В силу (4)
.
В силу (4) ![]() для некоторой
для некоторой ![]() ,
откуда следует, что элемент
,
откуда следует, что элемент ![]() реализует тип
реализует тип ![]() в модели
.
в модели
.
СЛЕДСТВИЕ. Полная теория , имеющая не более чем счетное множество неизолированных моделей имеет счетно-насыщенную модель.
ДОКАЗАТЕЛЬСТВО.
Всякий тип
реализуется в некоторой её счетной
модели, а каждая счетная модель реализует
не более счетного множества типов.![]()
5.
ТЕОРЕМА (единственности для счетно-насыщенных
моделей). Если
и
- счетно-насыщенные модели и ![]() ,
то
и
изоморфны.
,
то
и
изоморфны.
ДОКАЗАТЕЛЬСТВО.
Производная с помощью челночной
конструкции напоминает доказательство
теоремы единственности для атомных
моделей. Различие заключается в том,
что работаем с типами, а не с полными
формулами. Так как
и
- счетно-насыщены, то ![]() и
и ![]() можно занумеровать так, что
,
можно занумеровать так, что
,
![]() и всякий
и всякий ![]() ,
который в
,
который в ![]() реализуется
реализуется ![]() ,
.
Поэтому
,
.
Поэтому ![]() ,
откуда следует, что
,
откуда следует, что
![]() ,
задаваемый отображением
,
задаваемый отображением ![]() .
.
Модель называется счётно-универсальной, если счетна и всякая счетная модель , для которой , элементарно вкладывается в модель .
6. ТЕОРЕМА (о счётно-универсальных моделях). Всякая счетно-насыщенная модель является счетно-универсальной.
ДОКАЗАТЕЛЬСТВО.
Пусть
- некоторая счетная модель, а
- счетно-насыщенная, для которой
.
Пусть
.
Используя односторонний вариант
челночной конструкции и насыщенностью
,
получаем во множестве
такую последовательность ![]() , что
, что ![]() .
Отображение
.
Отображение ![]() и осуществляет элементарное вложение
в модель
.
и осуществляет элементарное вложение
в модель
.
Однако имеются счетно-универсальные модели, и являющиеся счетно-насыщенными.
Напомним, что
теория
называется ![]() -
категоричной,
если все её модели мощности
– изоморфны.
-
категоричной,
если все её модели мощности
– изоморфны.
7. ТЕОРЕМА (об описании - категоричных теорий).
Пусть - полная теория. Тогда следующие условия эквивалентны:
![]() является
– категоричной.
является
– категоричной.
![]() для всякого
теория
имеет лишь конечное число типов от
.
для всякого
теория
имеет лишь конечное число типов от
.
ДОКАЗАТЕЛЬСТВО. Установим цепь импликаций
![]()
Пусть выполнено
![]() и докажем
и докажем
![]() Теория
имеет модель
одновременно и счетно-насыщенную, и
атомную.
Теория
имеет модель
одновременно и счетно-насыщенную, и
атомную.
Пусть - единственная счетная модель . Она счетно-проста и поэтому атомная, а т.к. имеет не более счетного числа моделей (одну), то обладает счетно-насыщенной моделью, т.е. будет таковой.
Пусть выполнено и докажем
![]() Для всякого
каждый тип теории
содержит полную формулу.
Для всякого
каждый тип теории
содержит полную формулу.
В силу
– насыщенности модели
,
тип ![]() реализуется некоторой n-кой
.
Но
- атомная модель и поэтому на
выполняется некоторая полная формула
.
Но невозможно
реализуется некоторой n-кой
.
Но
- атомная модель и поэтому на
выполняется некоторая полная формула
.
Но невозможно ![]() ,
т.е.
.
,
т.е.
.
Пусть выполнено и докажем
Для всякого теория имеет конечное число типов от .
Обозначим через
множество отрицаний всех полных формул
теории
.
Его можно расширить до типа от
и значит ![]() не совместимо с
.
Поэтому уже некоторое конечное
не совместимо с
.
Поэтому уже некоторое конечное ![]()
![]() не совместимо с теорией
,
т.е.
не совместимо с теорией
,
т.е. ![]() откуда
откуда ![]() .
Для всякого
.
Для всякого ![]() множество
всех следствий теории
множество
всех следствий теории ![]() является типом в
.
Но в каждой модели
на каждой n-ке
выполняется одна из формул
является типом в
.
Но в каждой модели
на каждой n-ке
выполняется одна из формул ![]() и значит эта n-ка
реализует один из типов
и значит эта n-ка
реализует один из типов ![]() ,
т.е. список
,
т.е. список ![]() исчерпывает все типы
от переменных
.
исчерпывает все типы
от переменных
.
Путь выполнено и докажем
![]() Для всякого
с точностью до эквивалентности в теории
существует лишь конечное число формул
.
Для всякого
с точностью до эквивалентности в теории
существует лишь конечное число формул
.
Для всякой
обозначим через ![]() множество всех типов
теории
,
содержащих формулу
.
Тогда равенство
множество всех типов
теории
,
содержащих формулу
.
Тогда равенство ![]() влечет
влечет ![]() .
Но в
имеется лишь конечное число типов от
,
скажем
.
Поэтому существуют всего
.
Но в
имеется лишь конечное число типов от
,
скажем
.
Поэтому существуют всего ![]() множеств типов, а поэтому с точностью
до эквивалентности в
,
не более
формул.
множеств типов, а поэтому с точностью
до эквивалентности в
,
не более
формул.
Из выведем
![]() Все модели теории
атомные.
Все модели теории
атомные.
Пусть
– модель
,
и ![]() ,…,
,…,![]() конечный список всех (с точностью до
эквивалентности в
)
формул, выполняющихся на
.
Тогда
конечный список всех (с точностью до
эквивалентности в
)
формул, выполняющихся на
.
Тогда ![]() полная формула
,
выполняющаяся в
на
,
т.е.
- атомная.
полная формула
,
выполняющаяся в
на
,
т.е.
- атомная.
Пусть выполнено . Любые две счетные модели атомные и элементарно эквивалентны, а поэтому и изоморфны. Значит - - категоричная теория.
8. ТЕОРЕМА (о насыщенных и атомных моделях). Всякая полная теория , обладающая счетно-насыщенной моделью, имеет и счетную атомную модель.
ДОКАЗАТЕЛЬСТВО.
Предположим, что
не имеет счетной атомной модели. Тогда
сама теория
не является атомной. Поэтому существует
совместимая с
непополнимая формула
,
для которой можно подобрать такие
совместимые с
формулы ![]() и
и ![]() ,
что
,
что
![]() ,
, ![]() ,
,
![]() (*)
(*)
Формулы и также непополнимы. Повторяя аналогичные рассуждения, получим бинарное дерево непополнимых формул
![]()

![]()
![]()
![]()
![]()
Всякая бесконечная
последовательность ![]() из 0 и 1 определяет некоторую ветвь
из 0 и 1 определяет некоторую ветвь ![]() этого дерева. Всего существует
этого дерева. Всего существует ![]() ветвей. Согласно (*) каждая ветвь
ветвей. Согласно (*) каждая ветвь ![]() представляет собой совместимое с теорией
множество формул, а любые две ветви
несовместны друг с другом. Расширяя
каждую ветвь
представляет собой совместимое с теорией
множество формул, а любые две ветви
несовместны друг с другом. Расширяя
каждую ветвь ![]() до соответствующего типа теории
,
получим
различных типов. Поэтому для
нет счетно-насыщенной модели.
до соответствующего типа теории
,
получим
различных типов. Поэтому для
нет счетно-насыщенной модели.
9. ТЕОРЕМА ВОТА. Никакая полная теория не может обладать точно двумя неизоморфными счетными моделями.
ДОКАЗАТЕЛЬСТВО.
Выше показано, что
имеет счетно-насыщенную модель
и счетно-атомную модель
и они неизоморфные, поскольку
не атомная, в ней найдется n-ка
![]() ,
на которой не выполняется никакая полная
формула. Построим счетную атомную модель
,
на которой не выполняется никакая полная
формула. Построим счетную атомную модель
![]() полной теории
полной теории ![]() и покажем, что обеднение
и покажем, что обеднение ![]() этой модели не может быть ни
– насыщенной, ни атомным.
этой модели не может быть ни
– насыщенной, ни атомным.
Поскольку,
счетно-насыщена, такой же будет и ![]() .
Поэтому
.
Поэтому ![]() имеет счетно-насыщенную модель, значит
и счетно атомную
имеет счетно-насыщенную модель, значит
и счетно атомную ![]() .
Ее обеднение С – модель
,
которая не атомная потому, что n-ка
.
Ее обеднение С – модель
,
которая не атомная потому, что n-ка
![]() не удовлетворяет никакой полной формуле.
Поскольку
не
– категорична, она содержит бесконечно
много попарно неэквивалентных формул.
Поэтому и
содержит такие формулы, т.е. никакая
модель
не является одновременно атомной и
– насыщенной. В частности,
не удовлетворяет никакой полной формуле.
Поскольку
не
– категорична, она содержит бесконечно
много попарно неэквивалентных формул.
Поэтому и
содержит такие формулы, т.е. никакая
модель
не является одновременно атомной и
– насыщенной. В частности, ![]() не
– насыщенная и значит С не
– насыщенная.
не
– насыщенная и значит С не
– насыщенная.
