2. Доказать формулу Герона.

Т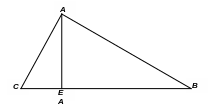 еорема Пифагора позволяет решить две важные задачи:

1) Зная стороны треугольника, найти его высоты;

2) Выразить площадь треугольника через его стороны.

Формула, устанавливающая связь между длинами сторон произвольного треугольника и его площадью, называется формулой Герона.

В треугольнике АВС: ВС = а; АВ = с; АС = b; AE  BC, AE = h_a; AE∩BC = {E};

CE = x; BE = a─x.

По теореме Пифагора из САЕ:

По теореме Пифагора из ВАЕ:

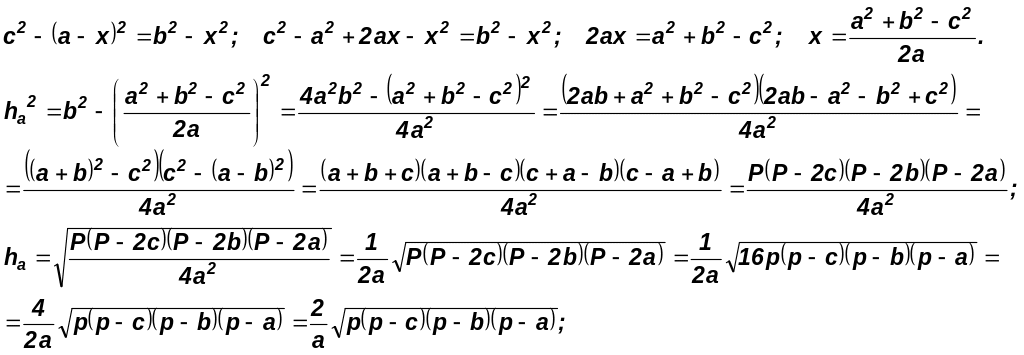
По аналогии запишем:

Найдем площадь АВC:

Билет № 9.

1. Взаимное расположение прямой и окружности.

Прямая и окружность могут находиться в следующих трех относительных положениях:

1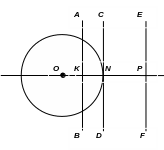 ) Расстояние OР от центра окружности до прямой EF, т. е. длина перпендикуляра, опущенного из центра на прямую, больше радиуса окружности: d > r. Точка Р удалена от центра окружности на расстояние, большее радиуса окружности, и потому лежит вне круга. Для любой другой точки прямой EF расстояние XO > PO > r (наклонные длиннее перпендикуляра), а значит, все точки прямой EF лежат вне круга; значит, прямая не имеет никаких точек, общих с окружностью.

2) Расстояние OK от центра окружности до прямой AB, т. е. длина перпендикуляра, опущенного из центра на прямую, меньше радиуса окружности: d < r. Точка K лежит внутри круга. Прямая AB пересекает окружность, т. е. имеет с ней две общие точки. Прямая OK называется секущей, а ее часть, состоящая из всех точек внутри окружности, является хордой окружности.

3) Расстояние ON от центра окружности до прямой CD, т. е. длина перпендикуляра, опущенного из центра на прямую, равно радиусу окружности: d = r. Точка N принадлежит и прямой, и окружности, все же остальные точки прямой, будучи удалены от О более, чем точка N, лежат вне круга. Значит, в этом случае прямая и окружность имеют только одну общую точку, которая служит основанием перпендикуляра, опущенного из центра окружности на прямую. Такая прямая называется касательной к окружности, а единственная общая точка прямой и окружности называется точкой касания.

2. Доказать формулу площади треугольника, выраженную через радиус вписанной окружности.

П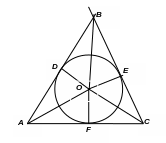 о свойству биссектрисы угла:

AB = c; BC = a; AC = b.

Площадь треугольника ABC:

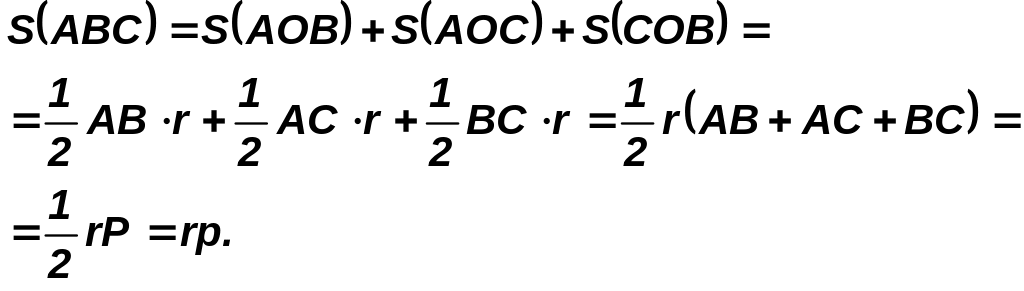
Билет № 10.

1. Доказать свойство касательной окружности. Следствие.

Определение 1. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.

Т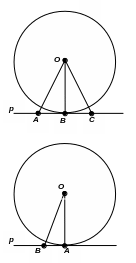 еорема 1 (о характерном свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

Доказательство:

Пусть прямая p касается окружности в точке А. Допустим, что прямая p не перпендикулярна ОА.

Проведем ОВp. Отложим на прямой p отрезок ВС = ВА. Тогда ΔАОВ = Δ СОВ как прямоугольные по двум катетам:

 OA = OC  точка С так же лежит на окружности, что противоречит условию. Следовательно, ОАp.

Теорема 2 (признак касательной, обратная). Прямая, проходящая через точку окружности и перпендикулярная ее радиусу, проведенному в эту точку, касается окружности.

Доказательство:

Возьмем любую точку А на окружности и проведем радиус ОА. Затем проведем прямую p, проходящую через точку А и перпендикулярную радиусу ОА. Любая точка В прямой p, отличная от точки А, удалена от О больше чем на радиус, поскольку наклонная ОВ длиннее перпендикуляра ОА. Следовательно, точка В не лежит на окружности. Значит, точка А − единственная общая точка прямой и окружности. Следовательно, прямая p является касательной к окружности.

Т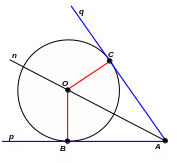 еорема 3 (об отрезках касательных, проведенных к окружности из одной точки). Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Доказательство:

По свойству касательных ОСq, OBp. Проведем луч из точки А через центр окружности. Рассмотрим образовавшиеся треугольники АОС и АОВ.

прямоугольные по гипотенузе и катету.

Из