2. Доказать формулу, выражающую площадь правильного многоугольника через его сторону, радиус вписанной и описанной окружностей.

Соединим центр многоугольника с его вершинами. Тогда многоугольник разобьется на n равных треугольников, площадь каждого из которых равна Следовательно,

И з рассмотрения равнобедренного треугольника получим:

Доказательство:

1) центральный, опирающийся на дугу, стягиваемую хордой А₁А₂;

2) Из ∆ А₁ОN₁ (А₁N₁О = 90°):

Отсюда

Билет № 4.

1. Сумма величин внутренних углов треугольника и многоугольника. Следствия.

1. Теорема о сумме углов треугольника.

Теорема: Сумма внутренних углов треугольника равна 180°.

Д ано: ∆АВС.

Доказать:

Доказательство:

1. Проведем

Свойства выпуклых многоугольников.

С войство 1. У выпуклого многоугольника все углы меньше 180°.

Доказательство: Возьмем любой угол А выпуклого многоугольника Р и его сторону а, идущую из вершины А. Пусть  - прямая, содержащая сторону а. Так как многоугольник Р выпуклый, то он лежит по одну сторону от прямой . Поэтому угол А лежит по одну сторону от прямой . Следовательно, угол А меньше развернутого, т. е. A < 180°.

Свойство 3. Сумма углов выпуклого многоугольника равна (n – 2)∙180°.

Доказательство (способ 1): Возьмем внутри выпуклого многоугольника Р произвольную точку О и соединим ее со всеми вершинами многоугольника. Образуется n треугольников, сумма углов каждого из которых равна 180°. Углы при вершине О в сумме дают 360° = 2∙180°. Поэтому сумма углов многоугольника равна n∙180° - 2∙180° = (n – 2)∙180°.

Доказательство (способ 2): Проведем из любой вершины выпуклого многоугольника Р все возможные диагонали, т. е. отрезки, соединяющие данную вершину со всеми несоседними вершинами. Диагонали разобьют многоугольник на (n – 2) треугольника. Заметим, что при сложении градусных мер углов полученных треугольников мы получаем сумму градусных мер углов выпуклого многоугольника. Сумма внутренних углов каждого треугольника равна 180°. Поэтому сумма углов многоугольника равна (n – 2)∙180°.

2. Правильные многоугольники. Доказать теорему о том, что около любого правильного многоугольника можно описать окружность и в любой правильный многоугольник можно вписать окружность.

Определение 1. Многоугольник называется вписанным в окружность, а окружность – описанной около многоугольника, если все вершины многоугольника лежат на окружности.

Около многоугольника можно описать окружность, если найдется точка, равноудаленная от всех его вершин. Эта точка лежит на серединном перпендикуляре каждой стороны многоугольника. Следовательно, около многоугольника можно описать окружность тогда и только тогда, когда серединные перпендикуляры всех его сторон имеют общую точку. Эта точка и будет центром описанной окружности.

Теорема 1: Около любого правильного многоугольника можно описать окружность, и притом только одну.

:

Дано: А₁А₂…А_n – правильный многоугольник.

Доказать: 1) существует окружность с центром О, описанная около многоугольника А₁А₂…А_n; 2) эта окружность единственная.

Доказательство:

1) Пусть лучи А₁О и А₂О – биссектрисы углов А₁ и А₂ – пересекаются в точке О. Докажем, что точка О – центр описанной около многоугольника А₁А₂…А_n окружности.

2) Рассмотрим ∆А₁ОА₂ – равнобедренный, т. к. по определению правильного многоугольника  по определению биссектрисы  Медиана ОN₁, проведенная к основанию равнобедренного треугольника, является высотой треугольника, т. е. серединным перпендикуляром.

3) Рассмотрим ∆А₁ОА₂ и ∆А₂ОА₃.

Из равенства треугольников 

4) Аналогично доказывается След-но, точка О равноудалена от всех вершин правильного многоугольника А₁А₂…А_n и является центром описанной окружности, а радиусом окружности является отрезок ОА₁.

5) Докажем, что эта описанная окружность единственная. Рассмотрим три любые вершины многоугольника, например, Так как через любые три точки, не лежащие на одной прямой, проходит только одна окружность, то около правильного многоугольника А₁А₂…А_n можно описать единственную окружность.

Определение 2. Многоугольник называется описанным около окружности, а окружность – вписанной в многоугольник, если все стороны многоугольника являются касательными к окружности.

В многоугольник можно вписать окружность, если найдется точка, равноудаленная от всех его сторон. Эта точка лежит на биссектрисе каждого угла многоугольника. Следовательно, в многоугольник можно вписать окружность тогда и только тогда, когда биссектрисы всех его углов имеют общую точку. Эта точка и будет центром вписанной окружности.

Теорема 2: В любой правильный многоугольник можно вписать окружность, и притом только одну.

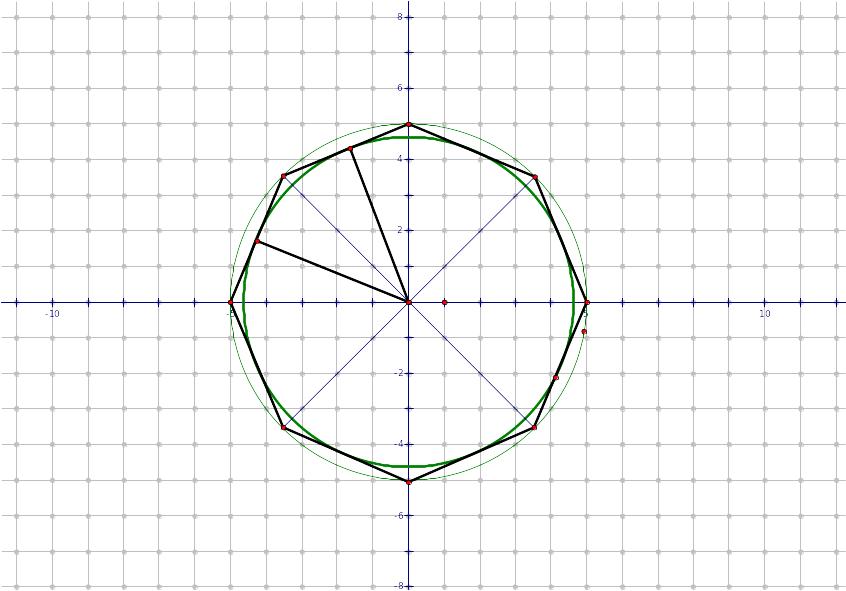
Дано: А₁А₂…А_n – правильный многоугольник.

Доказать: 1) существует окружность с центром О, вписанная в многоугольник А₁А₂…А_n; 2) эта окружность единственная.

Доказательство:

1) Из доказательства предыдущей теоремы следует, что серединные перпендикуляры Таким образом, окружность радиуса ОN₁ c центром в точке О является вписанной в многоугольник А₁А₂…А_n окружностью.

2) Докажем, что эта вписанная окружность единственная. Предположим, что наряду с рассматриваемой окружностью с центром в точке О и радиусом ОN₁ существует и другая вписанная в многоугольник окружность с центром в точке О₁. Тогда точка О₁ равноудалена от сторон многоугольника и лежит на каждой из биссектрис его углов, а следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. равен ОN₁. Таким образом, вторая окружность совпадает с первой.

Теорема доказана.

Следствие 1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах.

Следствие 2. Центр окружности, описанной около правильного многоугольника, совладает с центром окружности, вписанной в этот многоугольник. Эта точка называется центром правильного многоугольника.

Билет № 5.