1) Cd не пересекает окружность,

2) Cd пересекает окружность.

При первом предположении построим какую-нибудь касательную C₁D₁ к окружности, не пересекающую отрезок CD. Тогда по необходимому условию для описанного четырехугольника ABC₁D₁ имеем: AB + C₁D₁ = BC₁ + AD₁. Но т. к. BC₁ = BC − CC₁, AD₁ = AD − DD₁,

то AB + C₁D₁ = BC − CC₁ + AD − DD₁, откуда C₁D₁ + CC₁ + DD₁ = BC + AD − AB.

Из условия AB + CD = BC + AD следует BC + AD − AB = CD.

Следовательно, C₁D₁ +CC₁ +DD₁ =CD.

Оказалось, что в четырехугольнике CC₁D₁D одна сторона равна сумме трех других, что невозможно. Аналогично опровергается второе предположение. Теорема доказана.

Т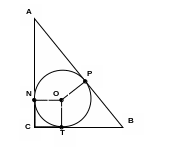 еорема о сумме катетов прямоугольного треугольника. Сумма катетов прямоугольного треугольника равна разности гипотенузы и диаметра вписанной окружности.

Доказательство:

По свойству касательных, проведенных к окружности из одной точки:

AN = AP, BP = BT, CN = CT = r.

AC = AN + r, BC = BT + r, AB = AP + PB.

AC + BC = AN + BT + 2r = AB + 2r.

a + b =c + 2r.

2. Доказать теорему о точке пересечения медиан треугольника.

Теорема о свойстве медиан треугольника. Три медианы пересекаются в одной точке. Эта точка делит каждую из медиан в отношении 2:1, считая от вершины.

Д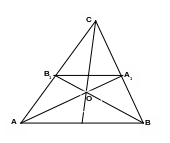 оказательство:

1). Медиана АА₁ пересекает АВ в точке А₁. Медиана ВВ₁ пересекает АС в точке В₁. Тогда А₁В₁– средняя линия.

2). Рассмотрим  АОВ и  А₁ОВ₁.

3). Из подобия треугольников:

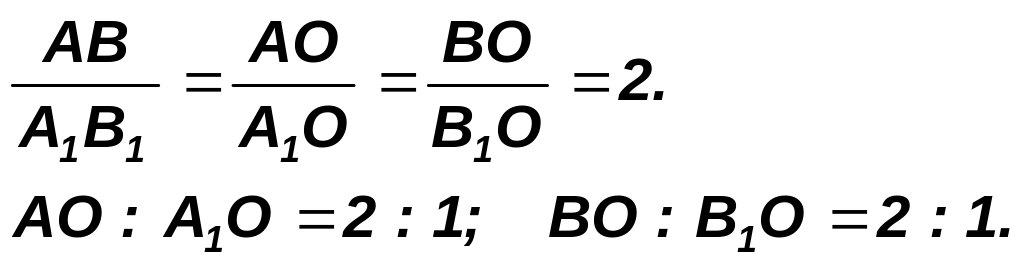
4). Аналогично доказывается, что точка О делит медиану СС₁ в отношении 2:1.

Билет № 16.

1. Подобные треугольники. Доказать теорему о прямой, параллельной стороне треугольника и пересекающей две другие его стороны.

В повседневной жизни часто встречаются тела и фигуры одинаковой формы, но разных размеров. В геометрии фигуры одинаковой формы принято называть подобными.

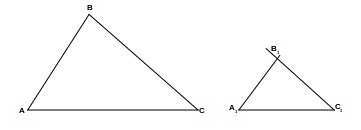Рассмотрим подобные треугольники АВС и А₁В₁С₁. У них углы соответственно равны и называются соответственными: А = А₁; В = В₁; С = С₁. Стороны, лежащие против равных углов, называются сходственными: АВ и А₁В₁; ВС и В₁С₁; АС и А₁С₁.

Определение подобных треугольников. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Иначе:

Число k, равное отношению сходственных сторон, называется коэффициентом подобия.

С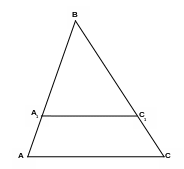 ледствие первого признака подобия. Прямая, параллельная какой-либо из сторон треугольника, отсекает от него треугольник, подобный исходному.

Доказательство:

Рассмотрим АВС и А₁ВС₁.

2. Доказать теорему о сумме квадратов диагоналей параллелограмма.

Теорема. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Д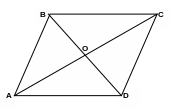 ано:

ABCD – параллелограмм;

AC ∩ BD = {O}.

Доказать:

Доказательство:

1. Рассмотрим BAD.

По теореме косинусов: где BАD = .

2. Рассмотрим ABC.

По теореме косинусов: где ABC = .

3. По свойству углов, прилежащих к одной стороне параллелограмма:

BAD + ABC = 180   +  = 180   = 180 − .

4. Преобразуем выражение для стороны AC, используя формулы приведения: так как по формуле приведения поскольку ABC = 180− находится во второй четверти.

5. Найдем сумму квадратов отрезков АС и ВD, являющихся диагоналями параллелограмма ABCD.

Поскольку по свойству параллелограмма BC = AD, то

Билет № 17.

1. Четыре замечательных точки треугольника. Доказать теоремы о центре тяжести и ортоцентре треугольника.

Замечательными точками треугольника являются:

1) Точка пересечения биссектрис треугольника. Она равноудалена от всех его сторон и является центром вписанной окружности. Точка пересечения биссектрис треугольника называется инцентром.

2). Точка пересечения серединных перпендикуляров к сторонам треугольника. Она равноудалена от всех его вершин и является центром описанной окружности.

3) Точка пересечения медиан треугольника. Она является центром тяжести треугольника.

3) Точка пересечения высот треугольника. Она является ортоцентром треугольника.

Теорема о центре тяжести треугольника. Все медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от соответствующей вершины.

Д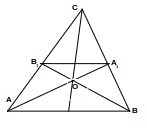 оказательство:

1). Медиана АА₁ пересекает АВ в точке А₁. Медиана ВВ₁ пересекает АС в точке В₁. Тогда А₁В₁– средняя линия.

2). Рассмотрим  АОВ и  А₁ОВ₁.

3). Из подобия треугольников:

4). Аналогично доказывается, что точка О делит медиану СС₁ в отношении 2:1.

Теорема об ортоцентре треугольника. Все высоты треугольника (или их продолжения) пересекаются в одной точке.

Д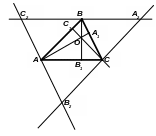 ано:  АВС; АА₁, ВВ₁, СС₁ - высоты.

Доказать: АА₁ ∩ ВВ₁ = {O}; АА₁ ∩ СС₁ = {O}.

Доказательство:

1. Проведем через каждую вершину треугольника прямую, параллельную противоположной стороне. Получим треугольник А₂В₂С₂.

2. Рассмотрим  АВС и  АВС₂.

2. Рассмотрим  АВС и  А₂ВС и аналогично докажем, что

3. Рассмотрим  АВС и  В₂АС и аналогично докажем, что

4.

5. Аналогично докажем, что АА₁ – серединный перпендикуляр к отрезку В₂С₂, а СС₁ – серединный перпендикуляр к отрезку В₂А₂.

6. Отрезки В₂С₂, В₂А₂ и А₂С₂ образуют треугольник А₂В₂С₂, в котором серединные перпендикуляры пересекаются в одной точке. Следовательно, высоты треугольника АВС пересекаются в одной точке.

2. Доказать теоремы о касательной и секущей, о двух секущих, проведенных из одной точки к окружности.

Т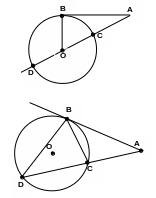 еорема 2. Квадрат отрезка касательной, проведенной из точки, лежащей вне круга, равен произведению отрезка секущей на ее внешнюю часть.

Доказательство:

1). Пусть секущая АD проходит через центр окружности О. Тогда OB – радиус окружности, AB – касательная к окружности. По свойству касательной OB  AB.

2). Из  AОB (ABO = 90°) по теореме Пифагора:

С

3). Пусть секущая AD не проходит через центр окружности. Построим вспомогательные хорды BC и BD.

4). Рассмотрим треугольники ABC и ABD.

Т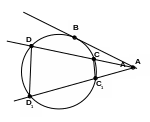 еорема 3. Если из некоторой точки А проведены к окружности сколько угодно секущих, то произведение каждой секущей на ее внешнюю часть есть число, постоянное для всех секущих.

Доказательство:

Проведем из точки А касательную к окружности. Тогда

Можно также доказать подобие треугольников ACC₁ и ADD₁.

Билет № 18.

1. Доказать признаки подобия треугольников.

Первый признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство:

1). Чтобы доказать подобие треугольников, нужно доказать, что их соответственные углы попарно равны и сходственные стороны пропорциональны.

2) Докажем равенство углов С и С₁:

3). Определим площадь АВС:

4). Определим площадь А₁В₁С₁:

5). Найдем отношение площадей данных треугольников:

6). По определению треугольники подобны:

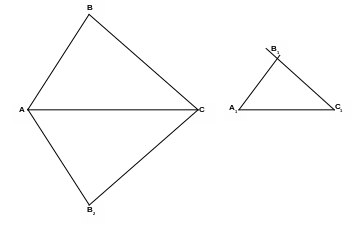
Второй признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство:

1). Рассмотрим треугольники АВС и А₁В₁С₁, у которых Нужно доказать, что еще одна пара углов, например в этих треугольниках равная, и тогда они подобны по первому признаку подобия.

2). Построим АВ₂С А₁В₁С₁. Для этого от стороны АС АВС отложим в нижнюю полуплоскость САВ₂ = А₁ и АСВ₂ = С₁. АВ₂С А₁В₁С₁ по первому признаку подобия.

3). Из подобия АВ₂С и А₁В₁С₁ следует: По условию Тогда

4). Рассмотрим треугольники АВ₂С и АВС:

5). Получим:

Третий признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство:

1). Рассмотрим треугольники АВС и А₁В₁С₁, у которых Нужно доказать, что одна пара углов, например в этих треугольниках равная, и тогда они подобны по второму признаку подобия.

2). Построим АВ₂С А₁В₁С₁. Для этого от стороны АС АВС отложим в нижнюю полуплоскость САВ₂ = А₁ и АСВ₂ = С₁. АВ₂С А₁В₁С₁ по первому признаку подобия.

3). Из подобия АВ₂С и А₁В₁С₁ следует: По условию Тогда

4). Из подобия АВ₂С и А₁В₁С₁ следует: По условию Тогда

5). Рассмотрим треугольники АВ₂С и АВС:

5). Получим:

2. Доказать теорему о площади прямоугольника, прямоугольного треугольника, теорему Пифагора.

Определение 1. Для многоугольных фигур площадью называется положительная величина с такими свойствами: 1) Если фигура составлена из нескольких многоугольных фигур, то ее площадь равна сумме площадей этих фигур. 2) Равные треугольники имеют равную площадь.

Определение 2. Фигуры, имеющие одну и ту же площадь, называются равновеликими.

Измерение площади состоит в сравнении площади данной фигуры с площадью фигуры, принятой за единицу измерения. В результате сравнения получается некоторое число, принятое за численное значение площади. Это число показывает, во сколько раз площадь данной фигуры больше (или меньше) площади фигуры, принятой за единицу измерения площади. За единицу измерения площади принимает площадь подходящего квадрата. Площадь этого квадрата называют квадратной единицей площади, а сам квадрат – единичным.

Т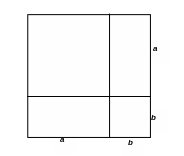 еорема о площади прямоугольника. Площадь прямоугольника равна произведению его сторон:

Доказательство: