Билет № 1.

1. Признаки равенства прямоугольных треугольников. Перпендикуляр и наклонная.

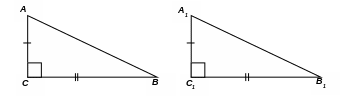
1. Если два катета одного треугольника соответственно равны двум катетам другого треугольника, то такие прямоугольные треугольники равны (частный случай первого признака равенства треугольников).

2 . Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).

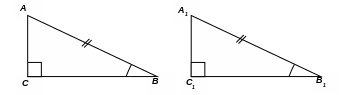
3. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

─ следствие из 2 признака равенства треугольников.

4. Если катет и противолежащий острый угол одного треугольника соответственно равны катету и противолежащему острому углу другого треугольника, то такие прямоугольные треугольники равны (частный случай второго признака равенства треугольников).

Доказывается аналогично предыдущей теореме ─ следствие из II признака равенства треугольников.

5. Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.

Доказательство:

1. Т. к. С = С₁, то АВС можно наложить на А₁В₁С₁ так, что вершина С совместится с вершиной С₁, а стороны СА и СВ наложатся соответственно на лучи СА₁ и СВ₁.

2. Т. к. СА = С₁А₁, то вершина А совместится с вершиной А₁. Остается доказать, что совместятся точки В и В₁.

3. Предположим, что точки В и В₁ не совместятся. Рассмотрим Δ А₁В₁В₂ – равнобедренный, так как АВ = A₁B₁  А₁В₂ = A₁B₁. Тогда A₁B₁В₂ = A₁В₂B₁. Заметим, что A₁B₁С₁ - острый угол прямоугольного треугольника А₁В₁С₁, а A₁B₁В₂, смежный с ним, - тупой. Поскольку в треугольнике не может быть двух тупых углов, то это невозможно. Значит, точки В и В₁ совместятся.

Пусть р – любая прямая и точка А не лежит на ней. Из точки А опустим перпендикуляр АС на прямую р.

О пределение 1. Точка С называется проекцией точки А на прямую р. Если точка А лежит на прямой, то ее проекцией на эту прямую является сама точка А. Точка С также называется основанием перпендикуляра АС.

Возьмем на прямой р точку В, отличную от точки С, и соединим точки А и В отрезком.

Определение 2. Отрезок АВ называется наклонной, проведенной из точки А на прямую р, а отрезок СВ называется проекцией наклонной АВ на прямую р.

Наклонная, проекция наклонной и перпендикуляр являются гипотенузой и катетами прямоугольного треугольника АВС. По т-ме Пифагора Поэтому Аналогично

С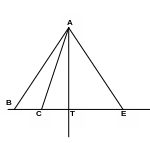 войство наклонной. Если из одной и той же точки проведены к некоторой прямой перпендикуляр и наклонная, то перпендикуляр и проекция наклонной всегда короче наклонной.

Теорема 1 (прямая). Если из одной точки проведены две наклонные к прямой, то большая наклонная имеет большую проекцию, меньшая наклонная – меньшую проекцию, равные наклонные имеют равные проекции.

Доказательство:

1) Рассмотрим АВТ и АСТ. АТВ = АТС = 90°; АТ – общая; AB > AC. Тогда по теореме Пифагора

2) Рассмотрим АВТ и АЕТ. АТВ = АТЕ = 90°; АТ – общая; AB = AЕ. Тогда по теореме Пифагора

Теорема 2 (обратная). Если из одной точки проведены две наклонные к прямой, то больше та наклонная, проекция которой больше.

Доказательство:

Рассмотрим АВТ и АСТ. АТВ = АТС = 90°; АТ – общая; BТ > CТ.

Тогда по теореме Пифагора

Определение 3. Расстоянием от точки А до фигуры F называется кратчайший отрезок, соединяющий любую граничную точку фигуры F с точкой А. Расстояние от точки А до фигуры F обозначается

Кратчайшим расстоянием от точки А до прямой р является перпендикуляр АС, опущенный из точки А на прямую р.

Определение 4. Расстоянием от точки до прямой называется перпендикуляр, опущенный из точки на данную прямую.

2. Вывести формулу площади круга, кругового сектора и сегмента.

О пределение 1. Кругом называется часть плоскости, ограниченная окружностью. Круг радиуса R с центром в точке О содержит точку О и все точки плоскости, находящиеся от точки О на расстоянии, не большем R.

Теорема 1 (о площади круга). Площадь S круга радиусом R выражается формулой S = R².

Пусть F – круг радиуса R, а Q – описанный около него правильный n-угольник. Тогда

Если число сторон многоугольника неограниченно возрастает, то его периметр сколь угодно мало отличается от длины окружности C = 2R, а площадь многоугольника сколь угодно мало отличается от площади круга.

Следствие 1. Площади кругов относятся как квадраты радиусов или диаметров.

Пусть S₁ и S₂ – площади кругов радиуса R₁ и R₂ соответственно. Тогда

Примечание 1. Квадратурой круга названа задача о построении циркулем и линейкой квадрата, равновеликого данному кругу, т. е. имеющего ту же площадь. Невозможность ее решения была доказана в конце XIX века.

Определение 2. Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Теорема 2 (о площади сектора). Площадь сектора равна произведению длины его дуги на половину радиуса:

Из чертежа очевидно, что площадь сектора зависит от градусной меры центрального угла, образованного радиусами, ограничивающими данный сектор. Она может быть определена как соответствующая часть площади руга.

Площадь сектора с центральным углом в 1° составляет часть площади круга, а площадь сектора с центральным углом в ° составляет часть площади круга и определяется по формуле: Преобразуем полученную формулу:

С ледует заметить, что площадь вектора однозначно определяется величиной центрального угла. Чем больше центральный угол сектора, тем больше длина дуги и, соответственно, площадь сектора.

О пределение 3. Сегментом называется часть круга, ограниченная дугой и хордой, соединяющими концы этой дуги.

Вывод формулы площади сегмента.

Из чертежа очевидно, что площадь сегмента может быть определена:

а) как разность площадей сектора 1 и треугольника AOB, если АОВ < 180°;

б) как сумма площадей сектора 2 и треугольника AOB, если АОВ > 180°.

Если градусная мера дуги АВ (соответствующего ей центрального угла) невелика, то площадь сегмента может быть определена по приближенной формуле: где b – есть основание сегмента или длина хорды АВ, а h – высота сегмента (стрелка сегмента). Стрелкой сегмента называется часть диаметра круга, перпендикулярного его хорде, лежащая в сегменте. h = CD. Если градусная мера дуги не превышает 50°, то погрешность в вычислении площади не превышает 1 %.

Билет № 2.