Математический анализ

1. Числа натуральные, рациональные и действительные. Полнота множества действительных чисел.

N назыв наименьшее из подмножеств R котор содержат 1 и вместе с каждым элементом содержат элемент на единицу больший т .е. n nN n+1N.(используются для нумерации элементов множества)

Множество всех натуральных, им противоположных и нуль назыв Z. Q- назыв мн-во всех чисел вида p/q где p .

2 мн-ва назыв эквивалентными если их можно поставить во взаимнооднозначное соответствие.

Мн-во назыв счетным если оно эквивалентно N

Т: R несчетно(т.к. оно имееют мощность континуума )

Док-во: докажем что даже мн-во всех R чисел (0;1) несчетно. Допустим что все эти числа перенумерованные 0; а1;а1- цифра 1й цифре после запятой у 1го из R чисел ; 0;а1;а2- цифра не равная 2й цифре после запятой у 2го из дейст-х чисел и так далее ; 0,a1a2a3…….

Мн-во R наз полным упорядочным полем, если для него выполняются след аксиомы:

1. Определена операция слож,т.е. 2 эл 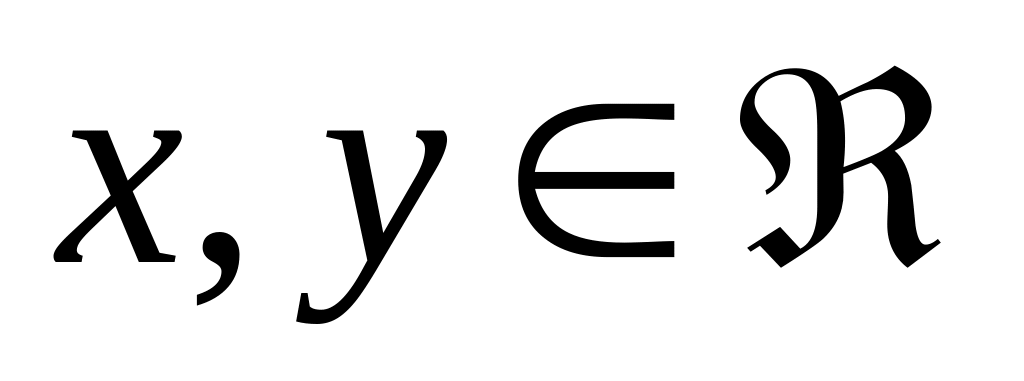ставит в соотв 3 эл , причём должны выполнятся аксиомы сложения:а) б) в) г)

2. Операция умнож а) б)

в) г)

3. 

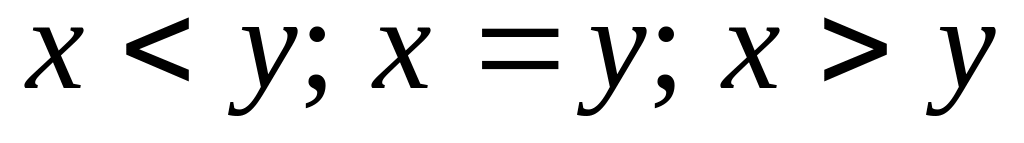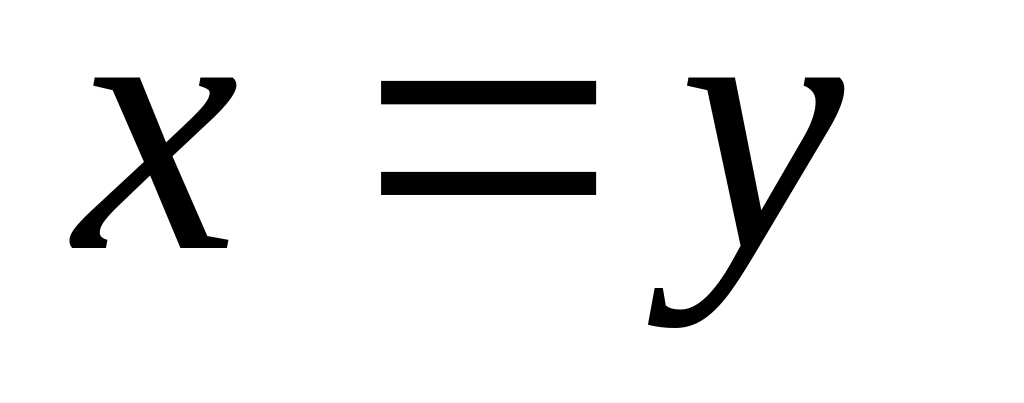4. Поле наз упоряд, если его эл определено одно из соотнош удовлетворяющее cв-вом: а) справедливо одно из след утвержд б)Если , то в) Если , то г) Если , то

д) Если , то

5) Полным упорядоч полем наз упоряд поле , если из того что не пустых

Опр: посл-ть фунд-на если  N n>=N m>=N  x_n-x_m  < (всякая сх-ся фундаментальна) (посл-ть назыв сх-ся если aR >0 N n>=N  x_n-a  < то есть а –предел посл-ти {x_n}

Т(о полноте д-х чисел): всякая фундаментальная последовательность д-х чисел сходится

Док-во: 3 этапа:1) докажем что всякая фунд-ная ограничена;2) тогда у нее есть сх-ся. Подпослед-ть ( если х_н-послед-ть и н_к-строго возр-щая пос-ть натур-х чисел ; тогда. Новая посл-ть х_н1 х_н2 …x_нк….-подпослед-ть исход послед-ти);3)докажем что вся посл-ть. Сходится к а (используя фундаментальность). Итак: (1) пусть =1 ; найдем номер из опр-я фундаментальности ; выберем м₀ >=N тогда. Для любого n>N x_n-x_m0<1; пусть А=min(x1,x2,…,xN,x_m0-1) тогда B=max(x1,x2,…,xN,xm0+1)тогда А<=xn<=B.(2): x_nka(3): рассмотрим любое е>0 , e/2;найдем номер из опр-я фундам-ти для е/2 выберем подпосл-ть так чтобы некот ее элемент н_к >=N ; x _nk-a/2. {x_nk}подпслед-ть значит {n }строго возрастающая натур. Значит n_k→∞ значит n_k>=N ; тогда для любого n>=N имеем │x_nk-x_n│<e/2 и │ x_nk-a│<e/2. Значит │x_n-a│=│(x_n-x_nk)+(x_nk-a)│<=│x_n-x_nk│+│x_nk-a│<e/2+e/2<e.

2. Последовательности и их сходимость (сходящиеся последовательности в топологическом пространстве; сходящиеся последовательности действительных чисел; теорема о существовании предела монотонной ограниченной последовательности; свойства последовательностей действительных чисел, связанные с арифметическими операциями над последовательностями).

Посл-тью чисел наз всякое отображение мн-во чисел во мн-во чисел, и обозначается (Посл-тью наз фунуция натур аргумента).

Число а наз пределом посл-ти x_n если >0 . Если послед. имеет предел, то эту послед. наз сходящейся, в противном случаи рассходящейся_..

Посл. наз огр.,если мн-во её значений огр. Посл. будет огр., если

Т:всякая сх-ся – ограничена

Д-во: пусть x_n→a положим =1; В=max(x ,…,x , a+1) НО обратное НЕВЕРНО.

Посл-ть- возраст-щая (убывающая), если . Возр. и убыв. послед. наз монотонными.

Т: всякая огр. посл-ть сходящаяся:1) если посл-ть возр и огр. сверху, то .

2) если посл-ть убыв и огр. снизу, то .

Д-во: пусть посл-ть возрастает и огран, это означает что , т.к. мн-во значений -огр,то это мн-во имеет sup . Пусть а=sup {x_n},докажем что ; рассмотрим >0 , поэтому имеем что , это означает что ЧТД.

Т(о связи предельного перехода с арифм операциями в множ-ве посл-тей):Если {x_n},{y_n}сх-ся посл-ти , то их сумма, произ-е,разность и частное явл. сх-ся посл-тями(в случае частного ,при допол предположении что предел Y_nне =0) .При этом lim(xn+yn)=lim xn+lim yn, lim(xn*yn)=lim xn*lim yn , lim(xn/yn)=lim xn/lim yn

Д-во(+): пусть xn→a, yn→b. Обозначим xn-a =pn, yn-b=qn тогда посл-ть рn ,qn б.м. (по лемме).Имеем xn+yn = a+pn+b+qn = (a+b) *(pn+qn); рn+qn б.м.(xn+yn)-(a+b) =p+qб.м., тогда посл-ть имеет предел а+b (для -,* аналогично). Для частного: xn→a ,yn→b ,b 0,док-ть что xn/yn→a/b.так как lim yn =b 0 , то все эл-ты посл-ти yn начин с некоторого номера будут 0.И будем рассматривать частное xn/yn только начиная с этого номера .рассмотрим

Это означает, что