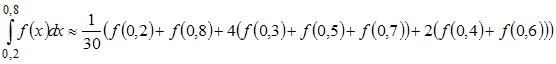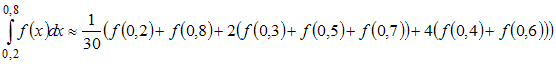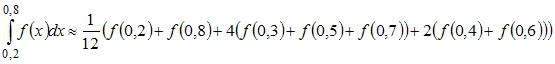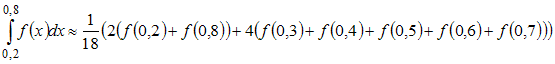- •4. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
- •6. Значение дифференцируемой функции в точке можно приближенно найти как …
- •7. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
- •16. Значение дифференцируемой функции в точке можно приближенно найти как …
- •20. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
- •22. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
- •30. Значение дифференцируемой функции в точке можно приближенно найти как …
- •33. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
- •35. Значение дифференцируемой функции в точке можно приближенно найти как …
- •37. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
- •38. Методом Эйлера с шагом решается задача Коши для системы дифференциальных уравнений с начальными условиями , . Тогда значения искомых функций и равны …
1. Интерполяционный
многочлен Лагранжа, составленный по
таблице значений функции
![]()
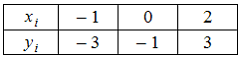 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Методом Эйлера
решается задача Коши
![]() ,
,
![]() с
шагом
с
шагом
![]() .
Тогда значение искомой функции
.
Тогда значение искомой функции
![]() в
точке
в
точке
![]() будет
равно …
будет
равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Метод
Эйлера решения задачи Коши
![]() ,
,
![]() реализуется
по следующим формулам:
реализуется
по следующим формулам:
![]() ,
,
![]() ,
,
![]() где
где
![]() –
шаг расчета (величина изменения
аргумента),
–
шаг расчета (величина изменения
аргумента),
![]() ,
а
,
а
![]() –
искомое решение задачи.
Значения
–
искомое решение задачи.
Значения
![]() и
и
![]() для
значения
для
значения
![]() определяются
начальным условием задачи Коши.
В
нашем случае
определяются
начальным условием задачи Коши.
В
нашем случае
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Требуется реализовать только один
шаг (этап) метода Эйлера, поскольку
.
Требуется реализовать только один
шаг (этап) метода Эйлера, поскольку
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
3. Значение
дифференцируемой функции
![]() в
точке
в
точке
![]() можно
приближенно найти как …
можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Воспользуемся
приближенной формулой
![]() .
В
нашем случае
.
В
нашем случае
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Тогда
.
.
Тогда
.
4. Интерполяционный многочлен Лагранжа, составленный по таблице значений функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Интерполяционный
многочлен Лагранжа 2-ой степени для
таблицы
 имеет
вид:
имеет
вид:
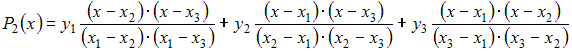 .
В
нашем случае получим:
.
В
нашем случае получим:
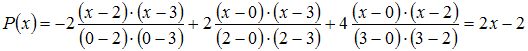 .
.
5. Методом Эйлера
с шагом
![]() решается
задача Коши для системы дифференциальных
уравнений
решается
задача Коши для системы дифференциальных
уравнений
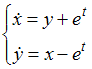 с
начальными условиями
с
начальными условиями
![]() ,
.
Тогда значения искомых функций
,
.
Тогда значения искомых функций
![]() и
и
![]() равны
…
равны
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Значение дифференцируемой функции в точке можно приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Воспользуемся
приближенной формулой
![]() .
Тогда
.
Тогда
![]() .
В
нашем случае
.
В
нашем случае
![]() ,
,
![]() и
и
![]() Следовательно,
получаем
Следовательно,
получаем
![]() .
.
7. Методом Эйлера решается задача Коши , с шагом . Тогда значение искомой функции в точке будет равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Метод
Эйлера решения задачи Коши
,
реализуется
по следующим формулам:
;
;
где
–
шаг расчета (величина изменения
аргумента),
,
а
–
искомое решение задачи.
Значения
и
для
значения
определяются
начальным условием задачи Коши.
В
нашем случае
![]() ;
;
;
;
![]() ;
.
Требуется реализовать два шага
(этапа) метода Эйлера, поскольку
;
.
Требуется реализовать два шага
(этапа) метода Эйлера, поскольку
![]() ;
;
![]() ;
;
![]() .
Тогда
.
Тогда
![]() .
.
8. Функция
![]() представлена
таблицей:
представлена
таблицей:
 Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами
Тогда
в интерполяционном полиноме Лагранжа
2-ой степени с узлами
![]() ,
составленном по этой таблице для
приближенного вычисления
,
составленном по этой таблице для
приближенного вычисления
![]() при
условии
при
условии
![]() значение
значение
![]() не
может быть равно
…
не
может быть равно
…
|
|
|
8 |
|
|
|
23 |
|
|
|
12 |
|
|
|
20 |
Решение:
Для
получения интерполяционного полинома
Лагранжа 2-ой степени требуются три узла
и
значения данной функции в них:
![]() .
Это могут быть любые три точки
из
таблицы, удовлетворяющие двум условиям:
.
Это могут быть любые три точки
из
таблицы, удовлетворяющие двум условиям:
![]() и
и
![]() .
Следовательно, в качестве узла
.
Следовательно, в качестве узла
![]() нельзя
брать 0, 1, 3, 4. Следовательно,
не
может принимать значения 2, 3, 5 или 8.
нельзя
брать 0, 1, 3, 4. Следовательно,
не
может принимать значения 2, 3, 5 или 8.
9. Метод левых
прямоугольников дает приближенное
значение интеграла
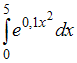 …
…
|
|
|
с недостатком |
|
|
|
с избытком |
|
|
|
точно |
|
|
|
про которое ничего определенного сказать нельзя |
10. На рисунке
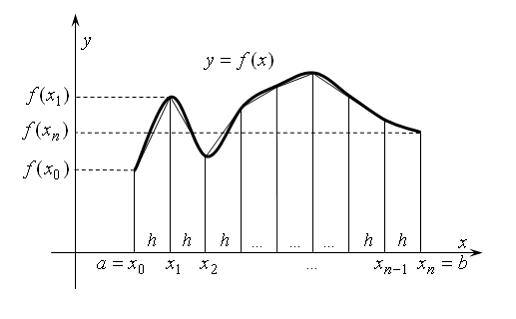 изображена
геометрическая интерпретация приближенного
вычисления определенного интеграла
методом …
изображена
геометрическая интерпретация приближенного
вычисления определенного интеграла
методом …
|
|
|
трапеций |
|
|
|
правых прямоугольников |
|
|
|
парабол |
|
|
|
левых прямоугольников |
Решение:
Как
известно, геометрический смысл
определенного интеграла от неотрицательной
непрерывной на отрезке
![]() функции
функции
![]() состоит
в том, что
состоит
в том, что
 равен
площади криволинейной трапеции,
ограниченной осью
равен
площади криволинейной трапеции,
ограниченной осью
![]() ,
прямыми
,
прямыми
![]() и
графиком функции
и
графиком функции
![]() .
Для получения приближенного значения
этой площади (этого интеграла) разобьем
отрезок
на
n
равных частей с длинами h
точками
.
Для получения приближенного значения
этой площади (этого интеграла) разобьем
отрезок
на
n
равных частей с длинами h
точками
![]() и
заменим каждую «маленькую» криволинейную
трапецию с высотой h
на обычную трапецию с высотой h
и основаниями, равными значениям функции
в левом и правом конце каждого частичного
отрезка –
и
заменим каждую «маленькую» криволинейную
трапецию с высотой h
на обычную трапецию с высотой h
и основаниями, равными значениям функции
в левом и правом конце каждого частичного
отрезка –
![]() и
и
![]() где
где
![]() Сумма
площадей полученных обычных трапеций
приближенно равна сумме площадей
маленьких криволинейных трапеций.
Данный метод замены
на
сумму
Сумма
площадей полученных обычных трапеций
приближенно равна сумме площадей
маленьких криволинейных трапеций.
Данный метод замены
на
сумму
 называется
методом трапеций приближенного нахождения
определенного интеграла.
называется
методом трапеций приближенного нахождения
определенного интеграла.
11. Решение
дифференциального уравнения
![]() на
отрезке
на
отрезке
![]() с
шагом
,
при начальном условии
,
в точке
по
методу Эйлера может быть найдено как …
с
шагом
,
при начальном условии
,
в точке
по
методу Эйлера может быть найдено как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Метод
Эйлера решения задачи Коши
,
реализуется
по следующим формулам:
,
![]() ,
где
–
шаг расчёта (величина изменения
аргумента),
,
а
–
искомое решение задачи.
Значения
и
для
значения
определяются
начальным условием задачи Коши.
В
нашем случае
,
где
–
шаг расчёта (величина изменения
аргумента),
,
а
–
искомое решение задачи.
Значения
и
для
значения
определяются
начальным условием задачи Коши.
В
нашем случае
![]() ,
,
,
.
Требуется реализовать только один
шаг (этап) метода Эйлера, поскольку
и
.
Тогда
,
,
,
.
Требуется реализовать только один
шаг (этап) метода Эйлера, поскольку
и
.
Тогда
![]() .
.
12. Значение
определенного интеграла
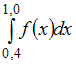 по
формуле парабол (Симпсона) можно
приближенно найти как …
по
формуле парабол (Симпсона) можно
приближенно найти как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. Функция
представлена
таблицей
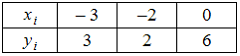 Тогда
значение
Тогда
значение
![]() ,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
,
вычисленное с помощью интерполяционного
многочлена Лагранжа, равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
6 |
Решение:
Интерполяционный
многочлен Лагранжа 2-ой степени для
таблицы
имеет
вид:
В
нашем случае получим:
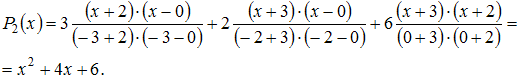 Тогда
Тогда
![]() .
.
14. Для задачи Коши
![]() выполнен
один шаг получения приближенного решения
методом Эйлера - Коши с шагом
:
выполнен
один шаг получения приближенного решения
методом Эйлера - Коши с шагом
:
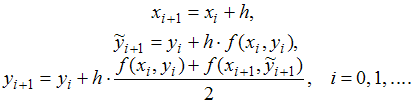 Тогда
значение
Тогда
значение ![]() ,
записанное с двумя знаками после запятой,
равно …
,
записанное с двумя знаками после запятой,
равно …
|
|
|
1,12 |
|
|
|
0,9155 |
|
|
|
1,11 |
|
|
|
1,1155 |
Решение:
По
условию задачи известно, что начальная
точка интегральной кривой имеет
координаты:
![]() .
Правая часть уравнения:
.
Правая часть уравнения:
![]() .
Получим следующую точку:
.
Получим следующую точку:
![]()
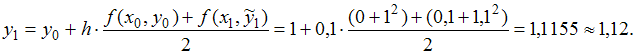
15. Функция
представлена
таблицей:
 Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
Тогда
график многочлена, интерполирующего
эту функцию, пересекает ось
в
точке с абсциссой …
|
|
|
5,5 |
|
|
|
11 |
|
|
|
6 |
|
|
|
0 |