Гидравлика, гидравлические машины и гидропривод: Лабораторный практикум. Издание переработанное и дополненное / Набережные Челны: Изд-во ИНЭКА. 2009 г. – с.

Составители: Г.Н.Толстухин, С.И.Харчук.

Лабораторный практикум содержит 6 лабораторных работ по общему и специальному курсам гидравлики, а также 4 работы по гидромашинам. Описание каждой лабораторной работы структурно включает в себя: цель работы, теоретические основы, описание установки, порядок выполнения работы, обработку экспериментальных данных и контрольные вопросы.

Ил.: Библ.назв.:

Рецензент: доцент Казанского государственного технического университета им. А.Н.Туполева (КАИ), к.т.н. В.М.Чефанов.

Печатается в соответствии с решением методической комиссии автомеханического факультета ГОУ ВПО «ИНЭКА».

Камская государственная

инженерно-экономическая

академия,2009г.

Введение

Настоящий лабораторный практикум является результатом опыта работы кафедры «Теплоэнергетика и гидропневмоавтоматика» ИНЭКА по циклу лабораторных работ, включенных в программы по гидравлике, гидравлическим машинам и гидроприводам.

Основным назначением практикума является ознакомление студентов с целью и теоретическими основами каждой работы, методикой проведения экспериментальных исследований и обработкой их результатов, а также усвоение и закрепление теоретического материала по отдельным разделам читаемых курсов: «Гидравлика и Гидрогазодинамика», «Гидравлика и гидромашины», «Гидравлика, водоснабжение и канализация»« и др.

Весь материал практикума разбит на отдельные работы и изложен в порядке их выполнения. В зависимости от специальности полный цикл лабораторного практикума по гидравлике и гидромашинам может содержать различное количество работ в соответствии с учебной программой курса. Поэтому практикум составлен так, что даже отсутствие ряда работ в том или ином курсе не повлияет на выполнение работ, предусмотренных программой. Для удобства пользования пособием все работы имеют однотипное построение. Подробное описание порядка выполнения работы, обработки экспериментальных данных и оформление работы с кратким изложением теоретических основ по каждой теме позволит студентам самостоятельно подготовиться к выполнению лабораторной работы. обучения.

Работа № 1

«Определение формы свободной поверхности жидкости в равномерно вращающемся вокруг вертикальной оси цилиндрическом сосуде»

ЦЕЛЬ РАБОТЫ

Определение формы свободной поверхности жидкости в цилиндри­ческом сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью и сопоставление результатов измерения с теоретическими расчётами.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

При вращении сосуда с жидкостью с постоянной угловой скоро­стью вокруг вертикальной оси в сосуде устанавливается состояние относительного равновесия (покоя) жидкости, т.е. такое состояние, при котором частицы жидкости не перемещаются относительно друг друга и самого сосуда, жидкость и сосуд движутся как одно целое.

Законы относительного равновесия жидкости находят широкое применение в различных областях техники - в металлургии (центро­бежное литьё), в измерительной технике (жидкостные тахометры) и др.

При исследовании относительного равновесия жидкости, наряду с установлением закона распределений давления в ней, практический интерес представляет определение формы поверхности равного дав­ления, т.е. такой поверхности, все точки которой испытывают одинаковое давление.

Дифференциальное уравнение поверхности равного давления имеет­ вид:

Xdx+Ydy+Zdz=0 (1.1)

где X,Y,Z - проекции ускорений массовых сил на соответствующие координатные оси;

dx, dy, dz - проекции приращения координат точки.

В случае относительного равновесия жидкости в цилиндричес­ком сосуде, вращающемся вокруг вертикальной оси с постоянной уг­ловой скоростью, на каждую частицу жидкости действуют две массо­вые силы: сила тяжести и центробежная сила инерции.

Рассмотрим в качестве поверхности равного давления свободную поверхность жидкости, в любой точке которой давление равно атмосферному. Проведём систему координат, вращающуюся вместе с сосудом, через вершину свободной поверхности жидкости (рис.1.1). При таком расположении осей проекции ускорений массовых сил, действующих, например, на частицу жидкости М, равны:

(1.2)

где: X,Y - проекции радиуса вращения точки М на координатные оси; - угловая скорость вращения.

Подставив найденные значения про­екции в уравнение (1.1) и проинтегрировав его, получим:

(1.3)

Выражение (1.3) есть уравнение параболоида вращения.

Из выражения (1.3) видно, что форма параболоида вращения не зави­сит ни от рода налитой в сосуд жидкости, ни от формы сосуда.

Рис.1.1.

ОПИСАНИЕ УСТАНОВКИ

Схема установки для изучения относительного покоя жидкости во вращающемся сосуде представлена на рис.1.2.

Цилиндрический сосуд 1 заполнен на 0,6 своей высоты трансформаторным маслом и приводится во вращение электродвигателем 3 через червячный редуктор 2.

Для измерения координат свободной поверхности предназначено измерительное устройство, содержащее измерительную иглу 4 и ка­ретку 5. При вращении рукоятки 6 каретка с измерительной иглой перемещается в горизонтальном направлении. Отсчет перемещений ре­гистрируется по шкале. Вертикальное перемещение измерительной иг­лы осуществляется при вращении рукоятки 7. На поверхности измери­тельной иглы нанесена шкала, по которой регистрируют вертикальные координаты свободной поверхности жидкости. Точность отсчета вер­тикальных перемещений не менее 0,5 мм.

Конструкция установки предусматривает регулирование частоты вращения сосуда с жидкостью в пределах 10-15 рад/с. Измерение частоты вращения производится при помощи электронного тахометра.

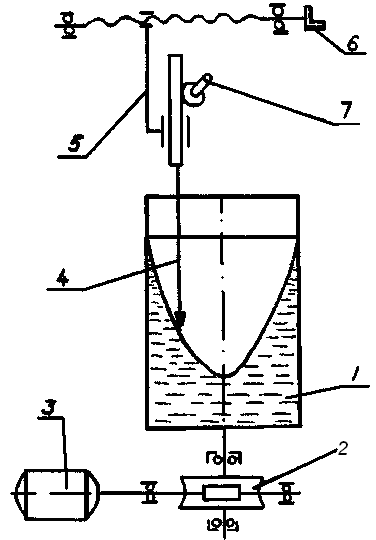
Рис.1.2.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Включением электродвигателя в сеть сосуд с жидкостью при­водится во вращение.

2. По стрелочному индикатору с помощью тарировочного графи­ка определяется частота вращения сосуда.

3. Игольчатым уровнемером определяют отметки в выбран­ных точках (7-10 точек) кривой свободной поверхности жидкости в сосуде с радиусом вращения . Отметку на оси вращения обозначим .

4. Данные измерений заносят в соответствующие графы таблицы.

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

1. По частоте вращения n сосуда подсчитывается угловая ско­рость вращения:

2. Вычисляются теоретические ординаты кривой поверхности

жидкости в сосуде:

3. По разности отметок точек свободной поверхности жид­кости и вершины параболоида, принятой за нулевую точку системы координат, определяются экспериментальные значения ординат сво­бодной поверхности в сосуде:

4. Вычисляется относительная погрешность измерений

Все вычисленные значения заносятся в соответствующие графы таблицы 1.1.

5. По данным измерений и вычислений вычерчиваются экспери­ментальная и теоретическая кривые свободной поверхности жидко­сти в меридиональном сечении сосуда.

6. Работа заканчивается выводами о результатах сопоставле­ния экспериментальной и теоретической кривых свободной поверх­ности и анализом возможных их несовпадений.

Таблица 1.1

Номер точки
Размерность	м	м	м	м	%
1
2
3
.
.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Зависит ли форма свободной поверхности от формы враща­ющегося сосуда?

2. Зависит ли форма свободной поверхности от рода жидкости?

3. Как расположена свободная поверхность по отношению к век­тору массовых сил?

Работа № 2

«Исследование режимов движения жидкости

в цилиндрической трубе»

ЦЕЛЬ РАБОТЫ

1. Установление опытным путём наличия двух режимов движения жидкости.

2. Определение по опытным данным значений чисел Рейнольдса при ламинарном и турбулентном режимах движения.

3. Определение момента смены режимов движения и подсчёт зна­чения критического числа Рейнольдса.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

В природе возможны два режима движения жидкости: ламинарный и турбулентный. Ламинарный режим движения характеризуется ярко выраженной упорядоченной слоистостью без перемешивания частиц жидкости, движущихся по прямолинейным или плавно изменяющимся траекториям (рис.2.1а).

Рис. 2.1

В другом случае движение отдельных частиц происходит по сложным траекториям, имеющим пространственную форму, что приводит к интенсивному перемешиванию жидкости и хаотическому, неупоря­доченному её течению. Такой режим движения жид­кости называется турбулентным. При турбулентном режиме происходят пульсации скорости и давления в данной точке потока жидкости (рис.2.1б).

Между ламинарным и турбулентным режимами находится область переходного режима. В этой области движение не­устойчиво и может принимать как ламинарный, так и турбулентный характер (рис.2.1в).

В 1883 году английским физиком О.Рейнольдсом на основе многочисленных опытов с разными жидкостями при различных скоростях и размерах потока установлено, что на режим движения жидкости ока­зывает влияние её вязкость, определяемая кинематическим коэффициентом , плотность , характерный линейный размер потока ℓ и средняя скорость υ. Исходя из теории подобия, эти факторы объединяются в безразмерный комплекс Re , названный числом Рейнольдса, который для цилиндрической трубы диаметром d имеет вид:

(2.1)

Для потоков некруглого сечения число Рейнольдса подсчитывается по так называемому гидравлическому радиусу:

, (2.2)

где: - гидравлический радиус,

S - площадь живого сечения,

П - смоченный периметр.

С физической точки зрения число (критерий) Рейнольдса представляет собой отношение сил инерции потока к силам трения при его движении.

Так как сила инерции , (2.3)

а сила трения , (2.4)

то, разделив Y на F, получим:

, (2.5)

где: V - объём жидкости,

S - площадь соприкосновения слоев жидкости,

ℓ - характерная линейная величина.

В зависимости от значения указанного соотношения устанавливается или ламинарный, или турбулентный режимы движения жидкости. Число Рейнольдса, соответствующее моменту смены режимов движения, называется критическим числом и обозначается Re_кр Как показыва­ют опыты, значение Re_кр не зависит от рода жидкости и для напорного движения в цилиндрической трубе с обычной шероховатостью стенок принимает значение Re_кр = 2320. При значении Re < Re_кр режим движения ламинарный, если Re > Re_кр - режим движения жидкости тур­булентный.

Необходимо отметить, что искусственно уменьшая возмущённость потока, особенно на входе в трубопровод, можно получить ламинар­ный режим при числах Рейнольдса, значительно превышающих значение Re_кр, например, для цилиндрических труб до Re = 5000 и даже больше. Однако в этом случае ламинарный режим движения весьма не­устойчив и при малейшем возмущении мгновенно переходит в турбулентный. Искусственным возмущением (турбулизацией) можно получить турбулентный режим при значениях Re < Re_кр, который также будет неустойчивым и перейдёт в ламинарный при прекращении действия возмущающего устройства.

В зависимости от режима движения жидкости существенно меня­ются сопротивление и теплопередача обтекаемых потоком тел. По­этому в инженерной практике установление режима движения являет­ся необходимым условием при гидравлических расчётах.

ОПИСАНИЕ УСТАНОВКИ

Схема экспериментальной установки представлена на рис.2.2.

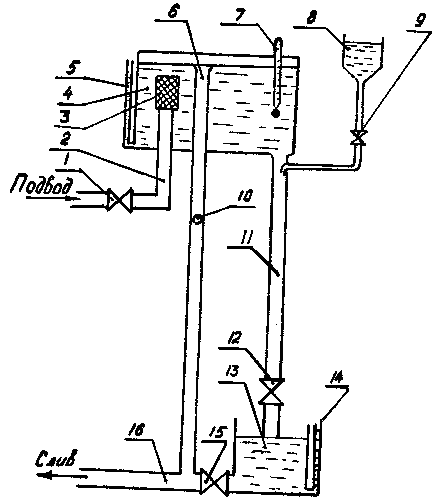
Рис. 2.2.

Вода из водопровода через вентиль 1 по трубе 2 с успокои­тельной сеткой 3 подаётся в расходный бак 4, уровень воды в котором контролируется водомерной трубкой 5. Во время экспери­мента уровень воды в баке поддерживается постоянным при помощи перепускного трубопровода 6, через который сливаются излишки воды. Наличие слива контролируется через смотровое отверстие 10, закрытое стеклом. Температура воды в баке определяется термомет­ром 7. Из расходного бака вода поступает в стеклянную трубку 11 диаметром 0,0245 м, установленную вертикально. На выходе стеклян­ной трубки установлен вентиль 12,с помощью которого регулируется скорость течения воды на экспериментальном участке. В начальный участок стеклянного трубопровода из бачка 8 тонкой струйкой по­даётся подкрашенная жидкость, расход которой регулируется краном 9. После стеклянного трубопровода жидкость поступает в мерный бак 13, имеющий мерную шкалу 14. Через кран 15 вода из мерного бачка сливается в сливной трубопровод 16.