Интегрирование рациональных функций

Из высшей алгебры известно, что всякую рациональную функцию можно представить в виде рациональной дроби, то есть отношения двух многочленов

Рациональная дробь называется правильной, если степень многочлена стоящего в числителе меньше степени многочлена, стоящего в знамена-теле

Рациональная дробь называется неправильной, если степень многочлена, стоящего в числителе больше или равна степени многочлена, стоящего в знаменателе

Если дробь неправильная, то разделив числитель на знаменатель по правилу деления многочленов, можно представить данную дробь в виде суммы многочлена и правильной дроби.

Здесь - многочлен, правильная дробь

Так как интегрирование многочленов проводится непосредственно и не вызывает затруднений, то в дальнейшем все наши рассуждения относительно интегрирования рациональных функций будут относится к правильным рациональным дробям.

Правильные дроби вида:

1. 

2. 

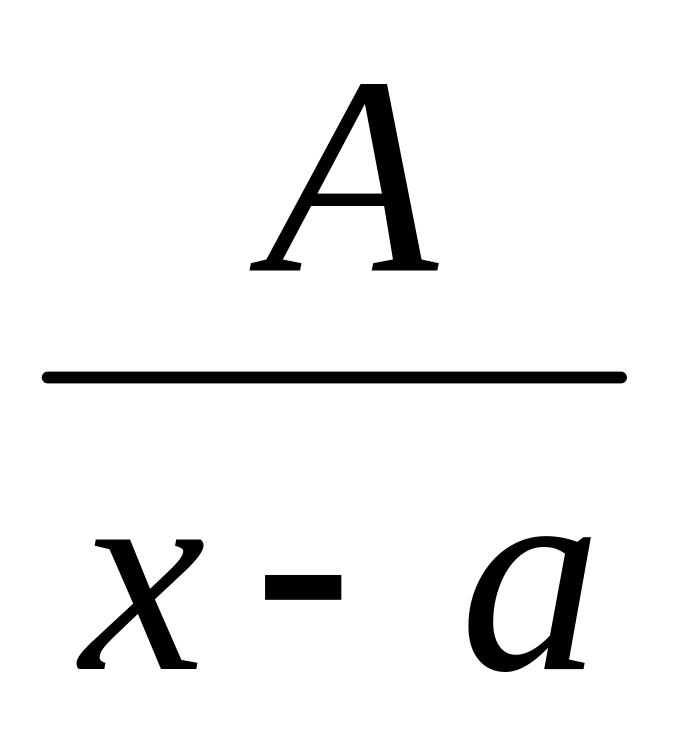
3. ( не имеет действительных корней)

Называются простейшими дробями.

Интегрирование простейших дробей I, II, III типов нами уже было рассмотрено ранее.

Теорема

Если знаменатель правильной рациональной дроби разложен на множители:

то дробь может быть представлена в виде суммы простейших дробей

Для определения коэффициентов применяют метод неопределенных коэффициентов. Сущность метода состоит в следующем:

В правой части разложения рациональной дроби простейшие дроби приводим к общему знаменателю, которым является многочлен , после чего знаменатель в левой и правой частях равенства отбрасываем. Получаем тождество, в левой части которого стоит многочлен , а в правой многочлен содержащий неопределенные коэффициенты . Приравнивая коэффициенты при одинаковых степенях в выражениях, стоящих в левой и правой частях тождества, получаем систему уравнений относительно искомых коэффициентов .

Например:

Найти интеграл

Подынтегральная функция в данном случае представляет собой неправильную дробь. Поэтому сначала представим её в виде суммы многочлена и правильной дроби. Для этого поделим многочлен на многочлен:

Будем иметь:

Далее воспользуемся методом неопределенных коэффициентов и разложим правильную дробь на сумму простейших дробей:

Приводим дроби к общему знаменателю и, отбросив его, получаем

Откуда, приравнивая коэффициенты при одинаковых степенях, получаем систему

Отсюда A= -1, B=1

Окончательно имеем

Следовательно

Пример 2

Напишем разложение подынтегральной дроби на сумму простейших дробей:

Приводим дроби к общему знаменателю и отбросив его, получаем

Приравнивая коэффициенты при одинаковых степенях получаем систему

Отсюда A=0, B=1, C=1, D=1

Тогда интеграл принимает вид

Интегрирование некоторых иррациональных выражений.

Интегрирование иррациональных выражений, вообще говоря, представляет большую трудность. Многие интегралы от иррациональных функций не выражаются через элементарные функции. Поэтому мы рассмотрим только некоторые частные случаи, когда заменой переменных можно от интеграла от иррациональной функции перейти к интегрированию рациональных выражений.

1.Рассмотрим интеграл вида

где R – рациональная функция, m, n, … p,q – целые числа

Пусть к - общий знаменатель дробей .

Применим подстановку

Тогда каждая дробная степень выразится через целую степень t и иррациональная функция преобразуется в рациональную

Например

Применим подстановку

2.Интегралы вида

вычисляются с помощью подстановки

где k - наименьшее общее кратное чисел n…q

Эта подстановка сведет интеграл от иррациональной функции к интегралу от рациональной дроби.

Например:

Обозначим тогда