Лабораторная работа №16

Санкт-Петербургский государственный электротехнический университет

КАФЕДРА ФИЗИКИ ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ N16 по дисциплине "Ф И З И К А" Маятники Преподаватель: студент гр. 0341 Юбрин А.Н. Санкт-Петербург 2000

Цель работы: Ознакомление с физическим маятником и определение ускорения силы тяжести при помощи оборотного маятника.

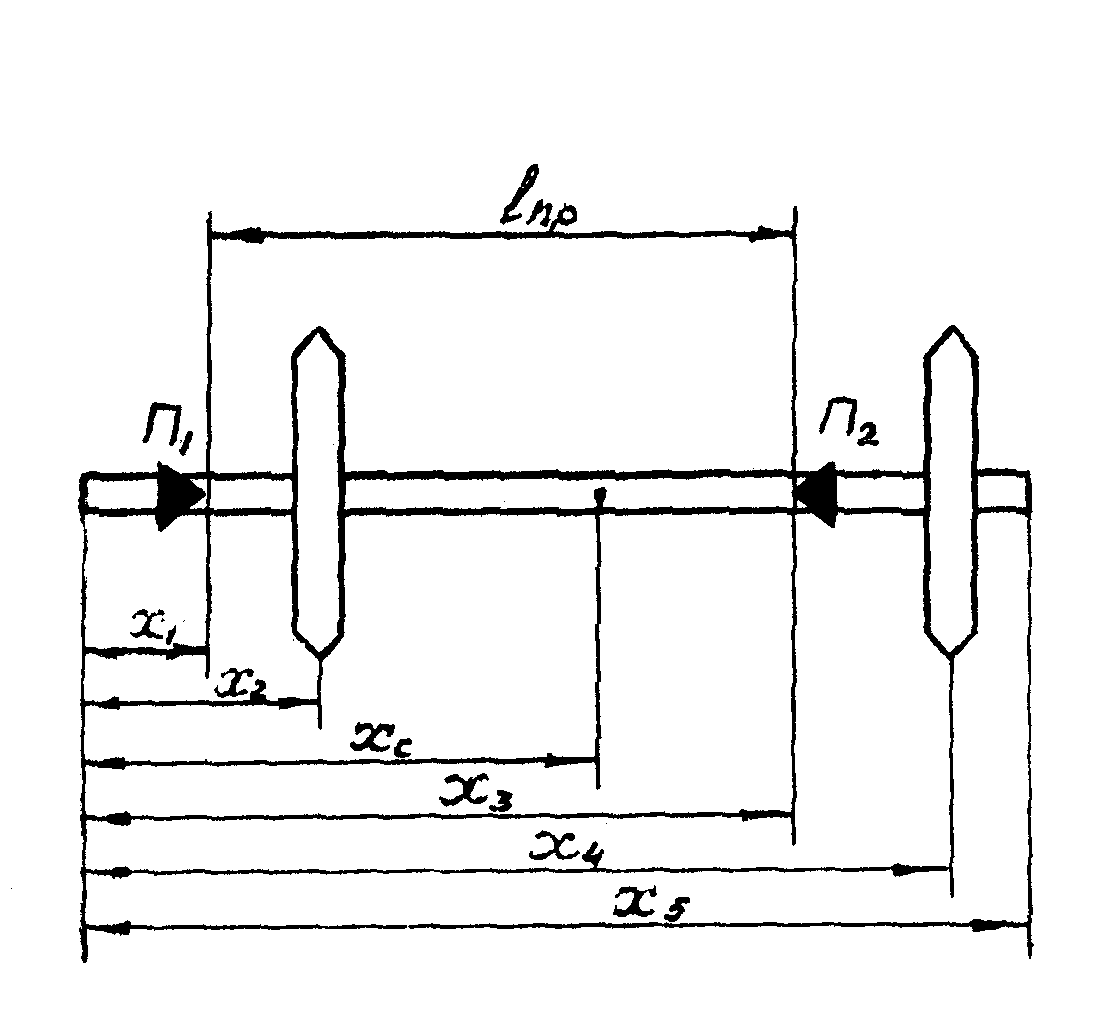Рисунок установки:

Приборы и принадлежности: Оборотный маятник, миллисекундомер, микрокалькулятор.

Исследуемые закономерности

Маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники:

• математический маятник – это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Период колебаний математического маятника Т не зависит от массы маятника m и определяется как:

, где l – длинна маятника; g – ускорение силы тяжести.

• физический маятник имеет подвешенную массу которую нельзя представить, как материальную точку. Период колебаний физического маятника определяется выражением:

, где J – момент инерции маятника относительно оси

качений(точка подвеса); m – масса маятника; l – расстояние от оси

качания до центра тяжести.

Используя две предыдущие формулы получается, что математический маятник с приведенной длинной будет иметь такой же период колебаний, как и данный физический маятник. Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Большинство косвенных методов измерения ускорения силы тяжести основано на использовании формулы для периода колебаний физического маятника. В данной лабораторной работе в качестве физического маятника, рассматривается оборотный маятник, состояний из стального стержня, на котором укреплены две опорные призмы П₁ и П₂. Период колебаний маятника можно менять припомощи подвижных грузов m₁ и m₂. Пусть удалось найти такое положение грузов при которых периоды колебаний маятника T₁ и Т₂ на призмах П₁ и П₂ совпадают, т.е.

Условием этого является равенство приведенных длин .

Исключая из предыдущей формулы J и m получаем формулу для g:

, где - расстояние между призмами П₁ и П_2, которое можно легко измерить.

Так как в реальных условиях T₁=Т₂ , поэтому для определения g при помощи оборотного маятника следует пользоваться формулой:

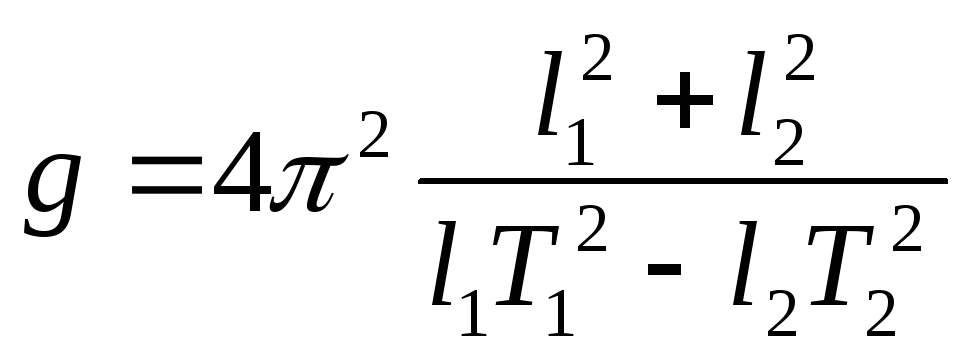
Для расчета необходимо предварительно найти центр масс x_c оборотного маятника. Для физического тела центром масс системы называется точка С, положение которой задается радиус-вектором :

, где m_i – масса i-й частицы; - радиус вектор, определяющий положение этой частицы; m – масса системы.

Задание по обработке результатов

Параметры маятника(см. рисунок)

Х1=0,04 м m1=1055 г

Х2=0,08 м m2=1061 г

Х3=0,44 м m3=396 г

Х4=0,49 м m=2512 г

Х5=0,55 м lпр=0.4 м

1. Статистическая обработка результатов измерений.

Расчет среднего T_1, T₂:

;

Расчет среднеквадратических отклонений:

;

;

Расчет случайной погрешности:

По Стьюденту:

t_P,N=2.8

;

Результат в округленной форме:

с вероятностью 95%

с вероятностью 95%

2. Ускорение силы тяжести по оценочной формуле:

- значения в таблице 1

3. Определение доверительной погрешности ускорения силы тяжести, найденной по оценочной формуле:

9.81-9.76=0.05

4. Нахождение цента масс маятника:

;

5. Расчет ускорения силы тяжести по уточненной формуле

6. Определение доверительной погрешности ускорения силы тяжести, найденной по оценочной формуле:

9.81-9.67=0.14

Вывод: Опыты показали, что g_расч=9.76, разница между истинным значением и расчетным обусловлена, малой точностью измерительных приборов и малым количеством измерений.