Лабораторная работа №4_2

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ОТЧЕТ

по лабораторной работе №4.2

"Исследование разветвленных цепей с применением компенсационного метода измерения"

Выполнил: Зуев Иван

Группа: 9132

Факультет: РТ

Санкт-Петербург

2000

Цель работы: ознакомление с компенсационным методом измерения на примере измерения ЭДС, приобретение навыков применения правил Киргофа для расчета разветвленных цепей.

Вспомогательный источник G3 с ЭДС ₃ создаст в цепи потенциометра R2 рабочий ток I₃. При замыкании кнопки SB1 в цепи устанавливаются токи I₁, I₂ , I₃. Первое правило Киргофа для узла А дает . По второму правилу для контуров A-G1-B-A и A-G3-C-B-A получим соответственно и , где R_x – сопротивление введенного участка потенциометра R2.

Когда сопротивление R_x равно нулю: I₁=0 получаем и . Изменяемая ЭДС компенсируется падением напряжения I₃R_x, создаваемым на сопротивление R_x током I₃, протекающего через потенциометр. Для этого вместо измеряемого источника G1 включают источник G2 с известной ₀ и добиваются ее компенсации (I₁=0), которая наступает при некотором, отличном от R_x. .

Для так называемых потенциометров, например реохордов, отношение R_x/R₀ равно отношению соответствующих координат движка n_x/n₀, отсчитываемых по шкале потенциометра, тогда

САНКТ-ПЕТЕРБУРГСКИЙ

ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

лабораторная работа№4.2

"Исследование разветвленных цепей с применением компенсационного метода измерения"

Протокол наблюдений

		1	2	3	4	5
G2 0	n0
G1 x	nx
G	nx

Выполнил: Зуев Иван Проверил:

Факультет: РТ

Группа: 9132

Санкт-Петербург

2000

По результатом наблюдений вычислим среднее значение и доверительные погрешности величин n₀, n_x, n`<sub>x</sub> и ЭДС <sub>x</sub> и `_x.

Для n₀, n_x, n`<sub>x</sub> считаем по СКО среднего: 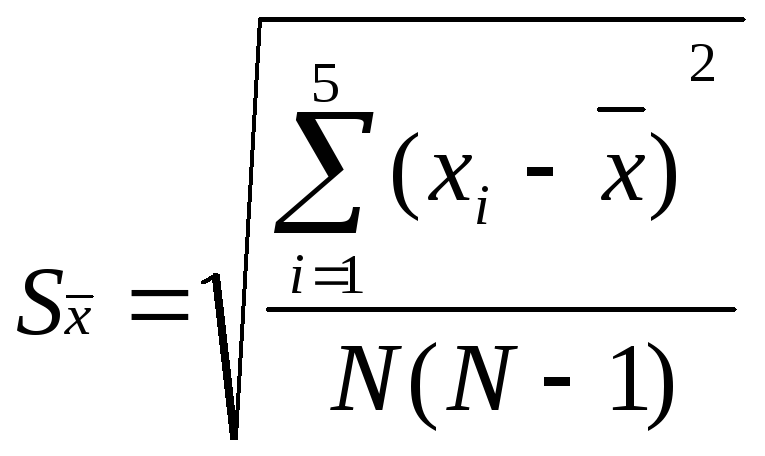, тогда для n<sub>0</sub> СКО равно: 0,380833. Результат для . В итоге получаем, что . Аналогичным путем найдем и для n<sub>x</sub>, n`_x и в результате получим следующее: и .

Для того, чтобы рассчитать ЭДС _x и `<sub>x</sub> нам надо, т.к. будет погрешность косвенных измерений формулу 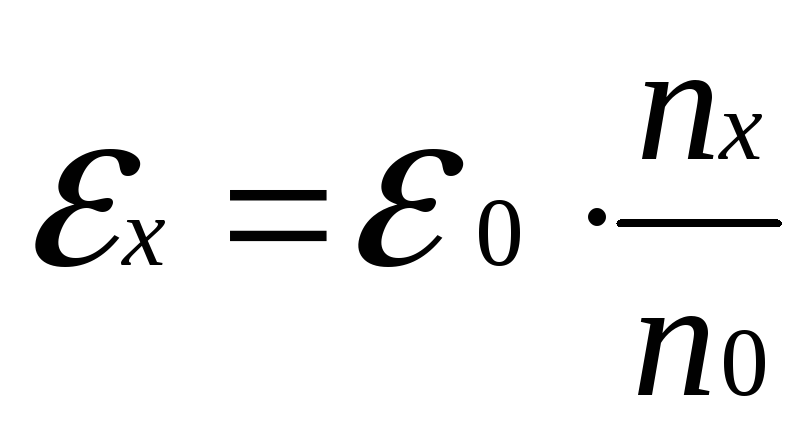прологарифмировать и взять производную: , тогда погрешность для <sub>i</sub> будет равна , аналогично и для `_x, в результате получаем, что В и В.

Можно сделать вывод, что включаемый в сеть источник R1 повлиял на результат, что он его немного снизил, но это уменьшение незначительно, поэтому он практически не влияет.

Рассчитаем _max: В.

Теперь определим внутренне сопротивление микроамперметра r₀ для микроамперметра, для этого составим по правилам Кирхгофа систему уравнений, пологая, что r₁=r₃=0:

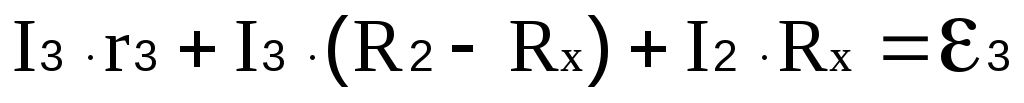
Т.к. и из второй формулы следует, что Ом.

	1	2	3	4	5	ср
G2 n0	170	170,5	169,5	171	171	170,4
G1 nx	255	254,5	254,5	254,5	255	254,7
G1 c R1	253,5	253	254	254	253,5	253,6
x	1,9125	1,903152	1,914381	1,897588	1,901315789	1,905787306
x`	1,90125	1,891935	1,910619	1,89386	1,890131579	1,897559236

Вывод: Исследованный в данной работе метод позволил нам определять показания  более точно, чем при прямом измерении вольтметром.