Лаба №3Измерение сопротивлений токопроводящих моделей при помощи моста Уитстона

ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНА.

Цель работы: ознакомление с методом измерения сопротивлений при помощи моста постоянного тока; приобретение навыков расчета сопротивлений проводников переменного сечения; определение удельных сопротивлений материалов токопроводящих моделей.

Приборы и принадлежности: стенд для сборки измерительной цепи; магазины образцовых сопротивлений; нуль-индикатор (гальванометр); источник тока.

Общие сведения: сопротивление проводников зависит от их формы и размеров, от рода вещества и его состояния. Для проводников в форме цилиндров постоянного поперечного сечения сопротивление равно:

,

где - удельное сопротивление материала проводника;

l и S – длина и сечение проводника, соответственно.

Удельное сопротивление является одной из основных электрических характеристик вещества. Оно определяет плотность тока в веществе при заданной величине напряженности электрического поля : , а также удельную тепловую мощность тока Р_уд., т.е. количество тепла, выделяющегося в единицу времени в единице объема:

Выражение (3.1) имеет ограниченное применение: оно не пригодно для проводников переменного сечения, в которых плотность тока не одинакова в любом сечении, например, при расчете сопротивления утечки цилиндрического конденсатора, заполненного проводящей средой. Расчет таких сопротивлений производят, разбивая проводники на множество элементов длинной и поперечным сечение S так, чтобы плотность тока в любой точке отдельного элемента была одинаковой. Сопротивление проводника на участке от l₁ до l₂ будет:

,

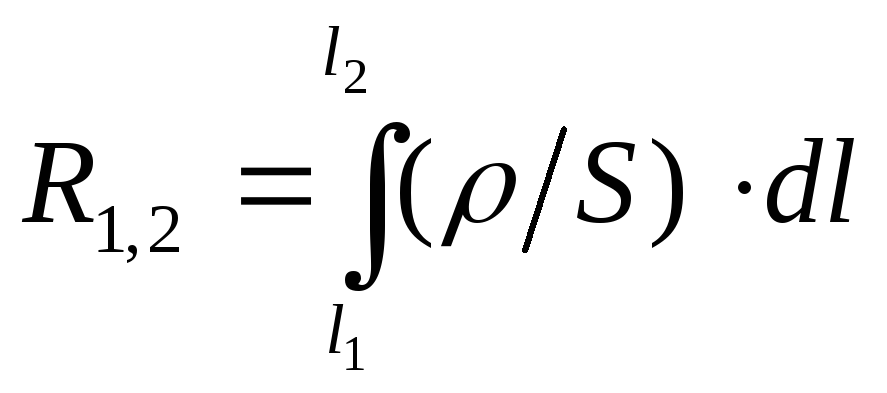где S – поперечное сечение проводника, представленное в виде некоторой функции от l.

Если такое разбиение невозможно, или зависимость S от l слишком сложна, используют подобие электрического поля в однородной проводящей среде с током электростатическому полю в диэлектрике при условии, что удельное сопротивление проводящей среды много больше удельного сопротивления материала электродов. Иначе говоря, распределение потенциала в проводящей среде с током окажется таким же, что и в диэлектрике, если, не меняя размера и формы электродов, их взаимного расположения и разости потенциалов между ними, проводящую среду заменить диэлектрической. При этом выполняется соотношение:

(3.2)

где R – сопротивление утечки между двумя электродами в проводящей среде с удельным сопротивлением ; C – емкость конденсатора, образованного этими же электродами в среде с относительной диэлектрической проницаемостью .

Таким образом, расчет сопротивления утечки между электродами в проводящей среде можно свести к расчету емкости конденсатора, образованного этими же электродами, т.е., по существу, к задаче электростатики.

Расчет емкости конденсатора производится по формуле , где Q – заряд на одном из электродов, - разность потенциалов между электродами.

Выражения для получается из связи напряженности и потенциала электрического поля ():

, (3.3)

где - проекция вектора на направление l, вдоль которого производится интегрирование. Линию l следует выбирать, руководствуясь соображениями простоты расчетов, например, удобно производить интегрирование вдоль одной из силовых линий электрического поля, так как при этом . Выражение для , подставляемое в формулу (3.3), находится по принципу суперпозиции напряженностей электрических полей и создаваемых зарядами электродов Q и –Q, либо по теореме Гаусса:

В результате расчета получается выражения для , представленное функцией заряда Q, геометрических размеров, формы и взаимного расположения электродов. В этом выражении коэффициент пропорциональности перед Q – есть величина, обратная емкости конденсатора, образованного электродами. Формула для расчета сопротивления утечки между электродами в проводящей среде получается из соотношения (3.2).

Следует также отметить, что из-за подобия распределения полей в проводящей среде и в диэлектрике проводящая среда может служить моделью для исследования электростатических полей. Например, вместо трудоемких расчетов или непосредственного измерения емкости какой-либо системы проводников сложной формы можно поместить модели этих проводников в проводящую среду, измерить сопротивление между ними, а затем найти емкость, использую соотношение (3.2). Во многих случаях такая методика оказывается предпочтительнее.

Методика измерений: в данной работе измеряются сопротивления токопроводящих моделей, имитирующие реальные объекты, например, сопротивление изоляции коаксиального кабеля, сопротивление утечки двухпроводной линии в проводящей среде, сопротивление заземления и так далее. Измеренные значения используются для расчета удельных сопротивлений материалов моделей .

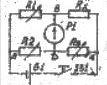Измерение сопротивления в работе производится при помощи моста постоянного тока (моста Уитстона). Измерительный мост (см. рис) образован четыремя резисторами: сопротивления трех из них – R1, R2, R3 – известны, а сопротивление четвертого - - требуется определить. Клеммами А и С мост присоединен к источнику G1, а в диагональ моста BD включен гальванометр P1.

Если сопротивление в плечах моста подобраны так, что напряжение делится между R1 и в ветви ABC в том же соотношении, что и между R2 и R3 в ветви ADC, то разность потенциалов между точками B и D равна нулю: нет тока через гальванометр (условие баланса моста), . Таким образом, зная значения R1, R2 и R3 при равновесии моста, можно определить неизвестное сопротивление

В качестве резисторов R1, R2 и R3 служат многодекадные магазины образцовых сопротивлений, изменяя номиналы которых, добиваются условия баланса моста, а затем рассчитывают значение . Измерения проводятся на двух моделях, имеющих сопротивления и . Переключатель SA1 обеспечивает включение в цепь моста либо сопротивления , либо .

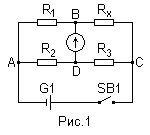
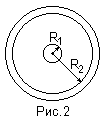
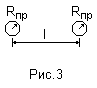
В данной работе в качестве токопроводящих моделей используются коаксиальный кабель и двухпроводная линия, поперечные сечения которых представлены на рисунках Рис.2, Рис.3 соответственно.

Размеры:

Коаксиальный кабель: R₁=4 мм, R₂=15 мм, h=80 мкм;

Двухпроводная линия: R_пр=2.5 мм, l=17 мм, h=0.16 мм.

Выведем формулы для _x1 и _x2

1. Для коаксиального кабеля.

RC=₀

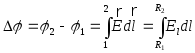
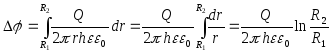
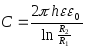
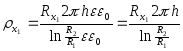
2. Для двухпроводной линии.

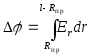
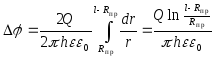
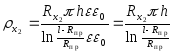
Таблица исходных данных

1. Вычислим для каждого R3 свой 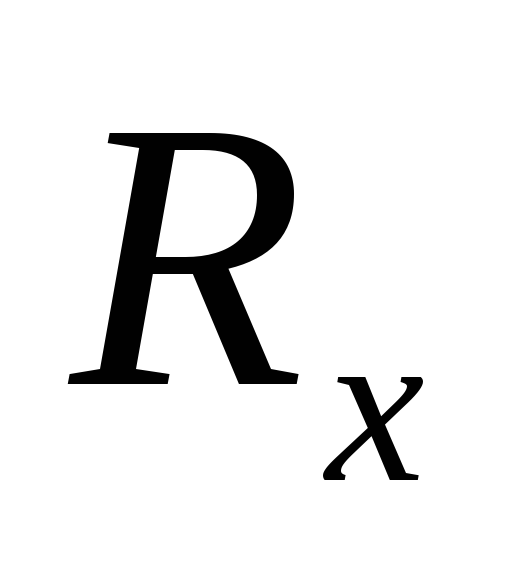и сведем значения в таблицу

	1:1	1:2	2:1
	1729	1746	1732
	1792	1808	1826

2. Вычисляем средние значения и погрешности искомых величин.

Для коаксиального кабеля.

R_x1=1736 (Ом)

	1	2	3
x1, Ом*м	0.657	0.663	0.658

_x1=0.660 (Ом*м)

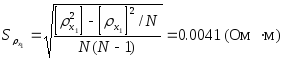
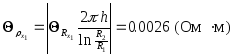
Для двухпроводной линии.

R_x2=1809 (Ом)

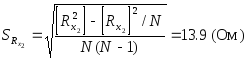
	1	2	3
x2, Ом*м	0.637	0.645	0.651

_x2=0.644 (Ом*м)

Ответ:

R_x1=(1.73  0.04)*10³ (Ом) _x1= 0.66  0.02 (Ом*м)

R_x2=(1.81  0.07)*10³ (Ом) _x2= 0.64  0.02 (Ом*м)

Вывод: В результате выполнения данной работы были получены результаты для _x1 и _x2, которые с учетом погрешностей перекрываются: _x1= 0.66  0.02 (Ом*м) _x2= 0.64  0.02 (Ом*м), т. е. в обоих случаях использовался один и тот же материал.

6