Лабораторная работа №17 по механике

Государственный комитет Российской Федерации по высшему образованию

С.-Петербургский Государственный Электротехнический Университет имени В. И. Ульянова (Ленина)

Лабораторная работа №17

Определение момента инерции маятника Максвелла

Выполнил: Кныш А.О.

(гр. 7201)

1998

1. Цель работы:

Изучение закона сохранения энергии и определение момента инерции маятника.

2. Описание приборов и установки:

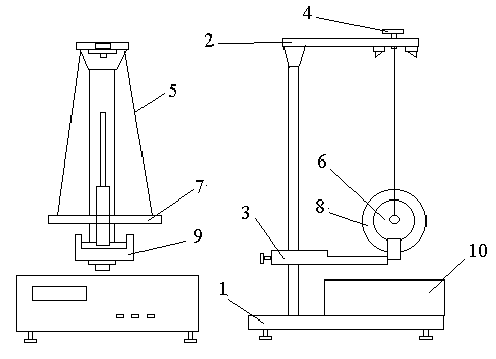
Маятник Максвелла (см. Рис.1) представляет собой диск 6, закрепленный на стержне 7, подвешенном на бифилярном подвесе 5 к верхнему кронштейну 2. На диске крепятся сменные кольца 8. Верхний кронштейн 2, установленный на вертикальной стойке 1, имеет электромагнит и устройство 4 для регулировки бифилярного подвеса. Маятник со сменными кольцами фиксируется в верхнем исходном положении с помощью электромагнита.

Рис. 1

На вертикальной стойке 1 нанесена миллиметровая шкала, по которой определяется ход маятника. На нижнем кронштейне 3 находится фотоэлектрический датчик 9. Кронштейн обеспечивает возможность перемещения фотодатчика вдоль вертикальной стойки и его фиксирования в любом положении в пределах шкалы 0...420 мм. Фотодатчик предназначен для выдачи электрических сигналов на миллисекундомер 10 в момент пересечения светового луча диском маятника.

3. Элементы теории:

Принцип работы маятника Максвелла основан на том, что маятник массой , поднятый на высоту путем накручивания нитей подвеса на стержень маятника, будет иметь потенциальную энергию . После отключения электромагнита маятник начинает раскручиваться и его потенциальная энергия будет переходить в кинетическую энергию поступательного движения и энергию вращательного движения . На основании закона сохранения механической энергии (если пренебречь потерями на трение):

(1)

где - ход маятника; - скорость маятника в момент пересечения оптической оси фотодатчика; _ - момент инерции маятника; - угловая скорость маятника в тот же момент времени.

Из уравнения (1) получаем:

.

Учитывая, что , , где - радиус стержня, - ускорение, с которым опускается маятник, получаем экспериментальное значение момента инерции маятника:

(2)

где - время хода маятника.

Теоретическое значение момента инерции мятника относительно оси маятника определяется по формуле:

(3)

где -масса стержня, =29г; -масса диска, насажанного на стержень, =131г; - масса сменного кольца; - внешний радиус диска; - внешний радикс кольца.

При учете работы, совершаемой маятником против сил трения, уравнение закона сохранения энергии имеет вид:

где -работа против сил трения.

Эту работу можно оценить по изменению высоты первого подъема маятника. Считая, что работа при спуске и подъеме одинакова, получим:

где -изменение высоты наивысшего положения маятника в первом цикле спуска-подъема. Тогда легко получить:

(4)

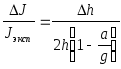
где - оценка величины, на которую завышается экспериментально определенное значение без учета потери энергии на трение.

Методика эксперимента:

Экспериментальное измерение основано на определении ускорения , с которым опускается маятник. Из уравнения (2):

(5)

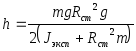
Проводится измерение времени опускания маятника с различной высоты , а затем методом наименьших квадратов определяется коэффициент линейной зависимости , где , . Из (2) определяется , а также погрешность .

Табл.1

4. Результаты эксперимента:

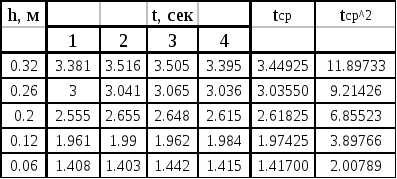
Табл.2

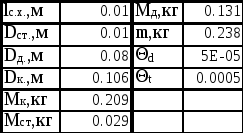
5. Обработка результатов эксперимента.

5.1. Нахождение коэффициента «k» зависимости y=kx, где y=h, x=t² и кго погрешности dk.

Нахождение коэффициента «k» осуществляется путем построения графика по данным табл.1.

По оси Ox - отложена величина t_ср.² вычисляемая по снятым данным а по Oy- h.

, получим таблицу:

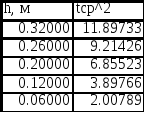
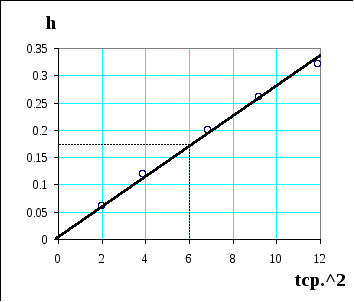
Для оценки погрешности вычислим значение для всех значений и по формуле:

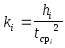, i=1...5.

В результате получим таблицу:

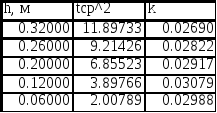
В результате можно перейти к обработке результата:

Пусть X=k, тогда

;; ; =0.0005

Расчет среднего значения результатов измерений:

, где N=5; =0.14496

0.14496/5= 0.02899

Проверка на промахи:

0.03079-0.02690= 0.00389

(0.02690-0.02822)/ 0.00389= 0.33934(0.02988-0.03079)/ 0.00389=

=-0.23274промахов в данных нет.

Расчет средне выборочного отклонения:

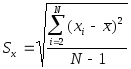, где N=5; 0.000009

= 0.00150

Вычисление среднеквадратичного отклонения: 0.00067

Расчет случайной погрешности по Стьюденту: 0.00067=0.00188

Расчет случайной погрешности по размаху выборки:=0.51×0.00389=0.00198

0.00198

Расчет полной погрешности: 0.00205=> округление результата должно производиться до сотых.

Результат в округленной форме:

Значение ускорения получаем из формулы: 0.06 м/с² , 0.001

5.2. Вычисление ( экспериментального значения момента инерции диска).

Вычисление производятся по формуле (2):

=0.00097 кг×м².

0.001.

= кг×м².

5.3. Вычисление (теоретического значения момента инерции).

Вычисление производятся по формуле (3):

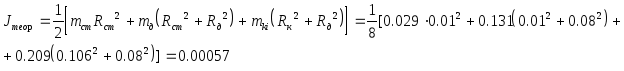
5.4. Нахождение ( погрешности вносимой трением).

Из соотношения (4) получаем:

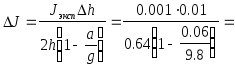0.00001.

5.5. Анализируя данные полученные в п.3 и п.4 можно сказать, что погрешность связанная с потерями энергии на трение очень мала и не вносит существенного вклада в общую ошибку.

6. Вывод по проделанной работе.

В результате проделанной работы был изучен закон сохранения энергии и определен момент инерции маятника кг×м².