
Лабораторная работа №32
.DOC
*

М
 инистерство
общего и профессионального образования
РФ
инистерство
общего и профессионального образования
РФ
Санкт-Петербургский Государственный
Электротехнический Университет
“ЛЭТИ”


кафедра физики
ОТЧЁТ
по лабораторной работе №№3
"“Исследование крутильных колебаний"”
Выполнил:
Группа: №9331
Факультет: КТИ
Проверил:
Шкирман И.А.
Мирошниченко Т.Я.
Санкт-Петербург
2000 год
Приборы и принадлежности: крутильный маятник, секундомер, масштабная линейка, штангенциркуль, микрометр.
Цель работы: определить параметры движения крутильного маятника, измерение модуля сдвига материала подвеса.
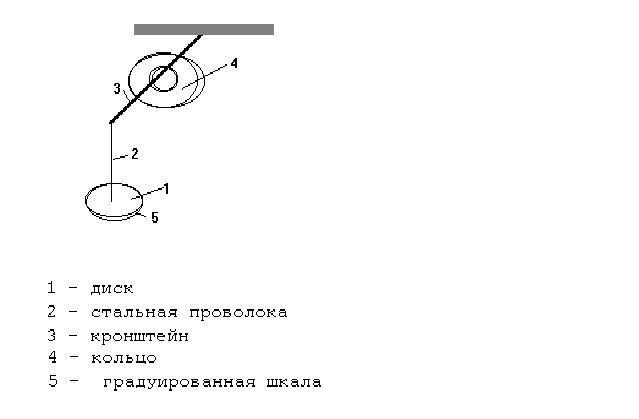
Устройство крутильного маятника: маятник представляет собой диск (1), закреплённый на толстой стальной проволоке, (2) свободный конец которой зажат в неподвижном кронштейне (3). На кроншейне расположено кольцо (4) известной массы, которое можно поместитьна диск. Для отсчёта угла поворота служит градуированная шкала (5), расположенная на основании маятника или диске.
рис. 1 Схема крутильного маятника
Основные
сведения изучаемого процесса:
При повороте тела, закреплённого на
упругом подвесе, на угол
происходит закручивание подвеса на тот
же угол, и в подвесе возникает возвращающий
момент упругих сил M=-k,
где k
- коэффициент кручения, зависящий только
от свойств подвеса. Без учёта трения в
повесе уравнение движения маятника
имеет вид
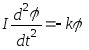 или
или
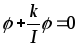 и
является уравнением осциллятора с
собственной частотой
и
является уравнением осциллятора с
собственной частотой
![]() .
.
Трение
в подвесе создаёт тормозящий момент
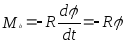 ,
где R
- коэффициент сопротивления. в этом
случае уравнение движения маятника
имеет вид I=-R-k
или
,
где R
- коэффициент сопротивления. в этом
случае уравнение движения маятника
имеет вид I=-R-k
или
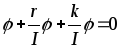 и
является уравнекнияем осциллятора с
затуханием. Решение этого уравнения
имеет вид
и
является уравнекнияем осциллятора с
затуханием. Решение этого уравнения
имеет вид
![]() ,
где А0
- начальная амплитуда колебаний маятника,
- время затухания, определяющее скорость
убывания амплитуды колебаний (А(t)=A0e-t/)
и численно равное времени, за которое
амплитуда уменьшается в е
раз
(рис. 2),
а w
- частота колебаний, связанная с
собственной частотой w0
соотношением
,
где А0
- начальная амплитуда колебаний маятника,
- время затухания, определяющее скорость
убывания амплитуды колебаний (А(t)=A0e-t/)
и численно равное времени, за которое
амплитуда уменьшается в е
раз
(рис. 2),
а w
- частота колебаний, связанная с
собственной частотой w0
соотношением
 .
Время затухания
может быть выражено и через механические
параметры маятника - момент инерции и
коэффициент сопротивления - соотношением
=2I/R.
.
Время затухания
может быть выражено и через механические
параметры маятника - момент инерции и
коэффициент сопротивления - соотношением
=2I/R.
 Энергия
колебаний, т.е. амплитудное значение
потенциальной (kA2/2)
или кинетической I(A)2/2
энергии, изменяется с учётом зависимоти
убывания амплитуды колебанийво времени
по закону W(t)=W0e-2t,
где W0=kA02/2
- начальная энергия колебаний. изменение
энергии происходит за счёт работы против
сил трения и превращения в теплоту
(диссипирует). скорость диссипации
энергии
Энергия
колебаний, т.е. амплитудное значение
потенциальной (kA2/2)
или кинетической I(A)2/2
энергии, изменяется с учётом зависимоти
убывания амплитуды колебанийво времени
по закону W(t)=W0e-2t,
где W0=kA02/2
- начальная энергия колебаний. изменение
энергии происходит за счёт работы против
сил трения и превращения в теплоту
(диссипирует). скорость диссипации
энергии
![]() есть мощность потерь
есть мощность потерь
![]() .
.
Кроме
времени затухания и мощности потерь
любая диссипативная система характеризуетя
также параметром Q
- добротностью, позволяющей судить о
способности системы сохранять энергию.
Величина добротности определяется
отношеием запасённой системой энергии
к потерям за время T/2=1/.
Тогда
 ,
т.е. добротность определяется числом
колебаний за время .
За это время амплитуда колебаний
уменьшается в
,
т.е. добротность определяется числом
колебаний за время .
За это время амплитуда колебаний
уменьшается в
![]() раза, а энергия - в
раза, а энергия - в
![]() раз.
раз.
методом
крутильных колебаний пользуются для
косвенного измерения модуля сдвига G
материала подвеся. модуль сдвига
характеризует упругие свойства материала
и в случае малых деформаций численно
равен силе, действующей касательно
площадке в месте определения модуляg
на единицу площади при единичном угле
сдвига
(рис. 3); G=Ft/S.
Величину
модуля сдвига определяют из соотношения
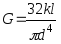 ,
где l
- длина подвеса, d
- диаметр, k
-
коэфиициент кручения.
,
где l
- длина подвеса, d
- диаметр, k
-
коэфиициент кручения.
РЕШЕНИЕ
1. Измерение линейных характеристик установки:
d (диаметр подвеса) = 2.5 мм = 0.0025 м
l (длина подвеса) = 600 мм = 0.6 м
Dex (внешний диаметр кольца) = 250 мм = 0.25 м
Din (внутренний диаметр кольца) = 60 мм = 0.06 м
DO (диаметр диска) = 250 мм = 0.25 м
m (масса кольца) = 1862 гр = 1.862 кг
2. Измерения колебаний маятника с/без кольца
в таблице протокола
3. Измерение времени затухания колебаний с/без кольца
в таблице протокола
4.1. Определение значения периода колебаний, вычисление погрешности периода с вероятностью 95% (без кольца):
|
Период Ti, c |
1.135 |
1.145 |
1.15 |
1.16 |
1.175 |
|
4.1.1. Проверка на промах
 ,
где R=|Tmax-Tmin|
,
где R=|Tmax-Tmin|
U95,5=0,64
![]() -
промаха нет
-
промаха нет
![]() -
промаха нет
-
промаха нет
4.1.2 Вычисление среднего значения
_
Т=1.153 с
4.1.3. Среднее квадратичное отношение:
|
_ T1-T |
_ T2-T |
_ T3-T |
_ T4-T |
_ T5-T |
|
|
|
-0.018 |
-0.008 |
-0.003 |
0.007 |
0.022 |
0.00093 |
0.00682 |
 =0.00682
c
=0.00682
c
4.1.4. Вычисление случайной погрешности:
Tсл=t95,5
t95,5=2.8
Tсл=0.00682*2.8=0.019 c
4.1.5. Вычисление полной погрешности:
T=Tсл+Т=0.019+0.005=0.069 c
T=0,069c
4.2. Определение значения периода колебаний, вычисление погрешности периода с вероятностью 95% (с кольцом):
|
Период T’i, c |
1.635 |
1.645 |
1.655 |
1.66 |
1.67 |
|
4.2.1. Проверка на промах
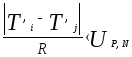 ,
где R=|T`max-T’min|
,
где R=|T`max-T’min|
U95,5=0,64
![]() -
промаха нет
-
промаха нет
![]() -
промаха нет
-
промаха нет
4.2.2 Вычисление среднего значения
_
Т’=1.653 с
4.2.3. Среднее квадратичное отношение:
|
_ T’1-T’ |
_ T’2-T’ |
_ T’3-T’ |
_ T’4-T’ |
_ T’5-T’ |
|
|
|
-0.018 |
-0.008 |
0.002 |
0.007 |
0.017 |
0.00073 |
0.006 |
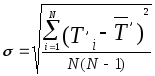 =0.006
c
=0.006
c
4.1.4. Вычисление случайной погрешности:
T’сл=t95,5
t95,5=2.8
T’сл=0.006*2.8=0.0168c
4.2.5. Вычисление полной погрешности:
T’=T’сл+T’=0.0168+0.05=0.0668 c
T’=0,0668 c
5. Определение времени затухания колебаний, вычисление доверительной погрешности с вероятностью 95% (без кольца):
|
i, c |
25.82 |
25.97 |
26.26 |
26.4 |
26.55 |
|
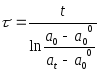
5.1. Проверка на промах
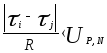 ,
где R=|max-min|
,
где R=|max-min|
U95,5=0,64
![]() -
промаха нет
-
промаха нет
![]() -
промаха нет
-
промаха нет
5.2 Вычисление среднего значения
_
=26.2 с
5.3. Среднее квадратичное отношение:
|
_ 1- |
_ 2- |
_ 3- |
_ 4- |
_ 5- |
|
|
|
-0.38 |
-0.23 |
0.06 |
0.2 |
0.35 |
0.3634 |
0.006 |
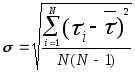 =0.1348
c
=0.1348
c
5.4. Вычисление случайной погрешности:
сл=t95,5
t95,5=2.8
сл=0.1348*2.8=0.8814c
5.5. Вычисление полной погрешности:
=сл+=0.8814+0.05=0.9314 c
=0.9314 c
6. Определение момента инерции маятника
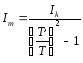 ,
где
,
где
![]()
![]()
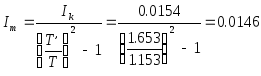
7. Нахождение 0,
![]()
![]()
![]() c-1
c-1
![]() c-1
c-1
8. Определение коэффициента кручения маятника
![]()
![]()
9. Расчет модуля сдвига
![]()
10. Нахождение полной энергии, мощности потерь и добротности маятника
![]()
W=7.83
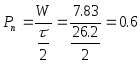
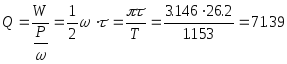
ПРОТОКОЛ
Таблица №1
|
Измеряемая величина |
Номер наблюдения i |
Результаты вычислений |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
|
||
|
Колебания диска без кольца |
||||||||
|
Число колебаний n |
20 |
20 |
20 |
20 |
20 |
|
||
|
Время колебаний t, c |
23.5 |
22.7 |
23.2 |
23.0 |
22.9 |
|
||
|
Период Ti, c |
1.175 |
1.135 |
1.16 |
1.15 |
1.145 |
|
||
|
Колебания диска с кольцом |
||||||||
|
Число колебаний n |
20 |
20 |
20 |
20 |
20 |
|
||
|
Время колебаний t, c |
33.2 |
32.9 |
33.4 |
32.7 |
33.1 |
|
||
|
Период T’i, c |
1.66 |
1.645 |
1.67 |
1.635 |
1.655 |
|
||
|
Масса кольца m= 1862 гр. Диаметры Dex= 250 мм ; Din= 60 мм ; D0= 250 мм ; Dпр= 0.5 мм t=0.05 c |
||||||||
Таблица №2
|
Измеряемая величина |
Номер наблюдения i |
Результаты вычислений |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
|
||
|
a0o, деления шкалы |
0 |
0 |
0 |
0 |
0 |
|
||
|
а0 , деления шкалы |
6 |
6 |
6 |
6 |
6 |
|
||
|
аt, деления шкалы |
3 |
3 |
3 |
3 |
3 |
|
||
|
t, c |
18.0 |
18.2 |
17.9 |
18.4 |
18.3 |
|
||
|
i, c |
25.97 |
26.26 |
25.82 |
26.55 |
26.4 |
|
||
Выполнил: Проверил: Шкирман И.А.
студент группы 9331, АСОиУ, ФКТиИ ............................................
24 февраля 2000 г. “..............” апрель 2000 год
