1.1.3.5 Введение в динамику системы
Систему материальных точек или тел, движение или равновесие которой рассматривается, называют механической системой. Если между точками (телами) механической системы действуют силы взаимодействия, то положение или движение каждой точки в ней зависит от положения и движения всех остальных. Классический пример - Солнечная система, в которой все тела связаны силами взаимного притяжения.
Действующие на механическую систему активные силы и реакции связей разделяют на внешние и внутренние.
Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы.
Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга.
Внутренние силы обладают следующими свойствами:
геометрическая сумма (главный вектор) всех внутренних сил системы равна нулю;
сумма моментов (главный момент) всех внутренних сил системы относительно любого центра сил или оси равна нулю.
Масса системы. Центр масс.
Масса системы равна арифметической сумме масс всех точек или тел, образующих систему
.
Распределение масс в системе определяется значениями масс тк ее точек и их взаимными положениями. В целом это распределение можно охарактеризовать некоторыми суммарными характеристиками. Ими являются координаты центра масс, осевые моменты инерции, центробежные моменты инерции. Чтоб определить эти понятия, нужно начать с определения центра тяжести.
Центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве. Координаты центра тяжести
;
;
,
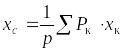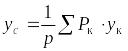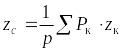где xк,
yк, zк
- координаты точек приложения сил тяжести
,
действующих на частицы тела;
Р - равнодействующая сил тяжести.
Учитывая, что
,
,
из этих уравнений следует
;
;
.
Эта замена справедлива лишь в однородном поле тяжести, для которого g = const. Геометрическая точка С, координаты которой определяются последними формулами, называется центром масс или центром инерции механической системы. Момент инерции относительно оси.
Моментом инерции тела (системы) относительно данной оси называется скалярная величина, равная сумме произведений масс всех точек тела на квадраты их расстояний от этой оси
.
В качестве примера приведем значения Jz для некоторых тел.Момент инерции тонкого однородного стержня длиной l, массой М относительно оси, перпендикулярной стержню и проходящей через ее конец
.
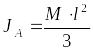Момент инерции тонкого круглого однородного кольца радиусом R, массой М относительно оси, проходящей через центр кольца перпендикулярно его плоскости
.
Момент инерции цилиндра относительно его оси
.
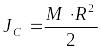Момент инерции сплошного шара относительно его оси
.
Использование приведенных выше понятий позволяет вывести для систем теоремы динамики, некоторые из которых мы рассматривали раньше применительно к точке.
1.2 Основные понятия о важнейших свойствах конструкций технических систем: прочности, жесткости и устойчивости
Прочность, жесткость, устойчивость формы являются предметом науки, называемой сопротивлением материалов, которая является составной частью механики твердого тела.