Глава 3. Проверка статистических гипотез

3.1. Статистическая гипотеза

Статистической гипотезой называют предположение либо о виде распределения генеральной совокупности (закон распределения неизвестен), либо о значениях неизвестных параметров известного закона распределения. Например, статистическими являются гипотезы:

1. генеральная совокупность распределена по закону Пуассона;

2. математическое ожидание а нормально распределенной генеральной совокупности равно числу а₀;

3. дисперсии двух нормальных совокупностей равны между собой.

Статистические гипотезы делятся на параметрические (в них говорится о значениях параметров известного распределения) и непараметрические (в них высказывается предположение о виде закона распределения). Например, гипотеза 1) является непараметрической, а гипотезы 2) и 3) – параметрическими.

Наряду с проверяемой гипотезой (ее называют нулевой или основной Н₀.) рассматривают и противоречащую ей гипотезу (ее называют конкурирующей или альтернативной Н₁). Нулевая и альтернативная гипотеза взаимно исключают друг друга. Процедура проверки применяется к нулевой гипотезе Н₀. Если в результате проверки нулевую гипотезу Н₀ оказывается целесообразней отвергнуть, то принимается альтернативная гипотеза.

Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что а  10. Коротко это записывают так: Н₀: а=10; Н₁: а10.

Простой называют гипотезу, содержащую только одно предположение. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Нулевая гипотеза – это простая гипотеза, в ней говорится о конкретных значениях параметров или о конкретном распределении. Альтернативная гипотеза сложная, в ней подразумевается бесконечно много возможностей.

3.2. Процедура проверки нулевой гипотезы.

Для проверки нулевой гипотезы используют специально подобранную случайную величину (выборочную статистику) К, точное или приближенное распределение которой известно в предположении справедливости нулевой гипотезы Н₀. Эта случайная величина К называется статистическим критерием.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается (оно называется критической областью или областью отвержения гипотезы), а другое – те значения, при которых она принимается (область принятия гипотезы).При справедливости нулевой гипотезы Н₀ вероятность того, что случайная величина К примет значения из области принятия гипотезы, велика, а вероятность того, что случайная величина К примет значения из критической области, мала. Вероятность попадания в критическую область называется уровнем значимости и обозначается буквой . Тогда вероятность попадания в область принятия гипотезы Н₀ равна .

По выборке, извлеченной из генеральной совокупности, вычисляют наблюдаемое значение критерия К – число К_набл. Если это число принадлежит критической области, то гипотеза Н₀ отвергается, как противоречащая опытным данным. Справедливой в этом случае считается альтернативная гипотеза Н₁. Если же число К_набл принадлежит области принятия гипотезы Н₀, то эта гипотеза считается согласующейся с опытными данными.

В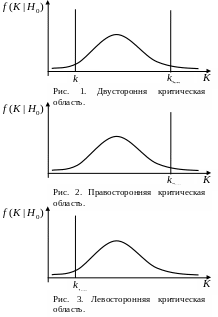 зависимости от условия эксперимента критическую область можно выбрать двусторонней, левосторонней и правосторонней. Критическая область строится в зависимости от вида конкурирующей гипотезы. Обозначим – плотность распределения случайной величины К при условии справедливости гипотезы Н₀.

Двусторонняя критическая область на рис. 1 образованна интервалами (– , k_1кр) и (k_2кр, ). Интервал (k_1кр, k_2кр) – область принятия нулевой гипотезы. Площади под кривой на интервалах (– , k_1кр) и (k_2кр, ) равны каждая.

Правосторонняя критическая область на рис. 2 образованна интервалом (k_2кр, ). Интервал (– , k_1кр) – область принятия нулевой гипотезы. Площадь под кривой на интервале (k_2кр, ) равна .

Левосторонняя критическая область на рис. 3 образованна интервалом (– , k_1кр). Интервал (k_2кр, ) – область принятия нулевой гипотезы. Площадь под кривой на интервале (– , k_1кр) равна .