5. Аксіоматичне означення імовірності. Властивості імовірностей

Нехай є простір елементарних подій, σ(сігма)-алгебра і імовірність для них (Ω, ,Р)

- сукупність підмножин простору елементарних подій Ω

1). ∀ А є Р(А)≥0;

2). Р(Ω)=1 (аксіома одиниці);

3). Аксіома зліченої адитивності:

А _і є , А_і ∩ А_j = Ø, і ≠ j

P( ) =

Властивості імовірностей:

1.1) Р(А) = 1 – Р(Ᾱ) 2) Ω = А ∪ Ᾱ 3) Р(Ω) = Р(А ∪ Ᾱ) = Р(А) + Р(Ᾱ)

2. Р(Ø) = 0 Ø є Ω , Р(Ø) = Р( ) = 1 – Р(Ω) = 1-1 = 0

3. А с В Р(В \ А) = Р(В) – Р(А) В \ А = В \ (А ∩ В) = В ∩ В = (В \ А) ∪ А Р(В) = Р(( В \ А) ∪ А) = Р(В \ А) + Р(А) Р( В \ А) = Р(В) – Р(А)

4. А с В Р(А) < Р(В) Р(В \ А) = Р(В) – Р(А)

Р(В \ А) ≥ 0 ,=> Р(В) – Р(А) ≥ 0 Р(В \ А) ≥ 0 ,=>

Р(В) – Р(А) ≥ 0 => Р(В) ≥ Р(А)

5. ∀ А є Р(А) ≤ 1 А с Ω Р(А) ≤ Р(Ω) =1

6. ∀ А, В є Р(А ∪ В) = Р(А) + Р(В) – Р(А ∩ В) А ∪ В = А ∪ (В\(А ∩ В)) Р(А ∪ В) = Р(А) + Р(В\(А ∩ В)) = Р(А) + Р(В) – Р(А ∩ В)

7. А₁ , А₂ ,…А_n є Р(В ∪ А_n) = Р(А_n) + Р(В) – Р(А_n ∩ В) Р ( ) = + )+…+ (-1)ⁿ P(A₁ ) Р(А ∪ В) = Р(А₁) + Р(A₂) – Р(А₁ ∩ A₂)

P( ) = P( ∪ A_n) = P(B ∪ A_n) = P(B) + P(A_n) – P(B ∩ A_n)

P(B) =

P(B ∩ A_n) = P(( )∩ B) = P( ∩ A_n)) = P( = 8. Теорема неперервоності для ймовірностей

Послідовність подій: - монотонно зростаюча, якщо

А₁≤ А₂≤ А₃≤ А₄≤….. А_n≤ А_n+1≤…

- монотонно спадна, якщо А₁≥ А₂≥ А₃≥ А₄≥….. А_n≥ А_n+1≥…

6.Умовні ймовірності.Приклади

Властивості:

1. P(A/A)=1 2. P(A/Ω)=P(A) 3.P(Ω/A)=1 4. P(A/B)>=0

5. 

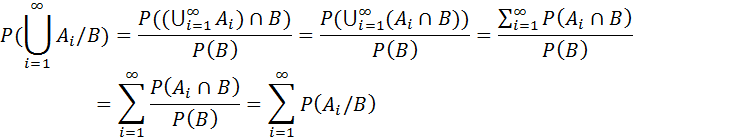
Теорема множення ймовірностей подій

(*)

Узагальнена ф-ла множення ймовірностей

….

Якщо покласти ( , отримаємо (*)

Дві події А і В наз. незалежними,якщо

Дві події А і В незалежнi,якщо

Приклад1. 2 гр.кубика , якщо на 1-му випала 1-ця?

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

Позн , P(B)>0

,P(A)>0

\ P(A)>0,P(B)>0

Приклад2 2 гр. кубика

А-парна кількість очок, В – непарна. Незал?

Події незалежні.

7.Формула повної імовірності та формула Байєса.

Формула Байєса.

_{Подія А може відбутись одночасно з деякою із подій . Відомі ймовірності подій та умовні ймовірності того, що подія А відбудеться. Відомо, що в результаті випробування подія А відбулась. Потрібно з огляду на це переоцінити ймовірності гіпотез . Для цього застосовують формулу Байєса. Нехай - усі гіпотези та несумісні події. (i = 1, 2,…n). Подія А відбувається хоча б з однією із подій, тоді:}

_{– це апріорна ймовірність;}

_{– це апостеріорна ймовірність;}

_{Доведення:}

_{Формула повної ймовірності:}

_{Нехай подія А може відбутися тільки за умови настання однієї із несумісних подій (i=1,2,…,n), які утворюють повну групу.}

_{Тоді ймовірність події А подається формулою:}

_{Доведення:}

8.Незалежні події

Def. Дві події А і В називаються незалежними якщо ймовірність добутку дорівнює добутку ймовірностей ( теорема множення незалежних подій):

P(A*B) =P(A)*P(B) або P(A∩B)=P(A)*P(B)

Тоді P(A/B) = P(A*B)/P(B) = P(A)*P(B)/P(B) = P(A);

P(B/A) = P(B*A)/P(A) = P(A)*P(B)/P(A) = P(B);

Властивості незалежних подій:

1Якщо А і В – незалежні події то А і В̅ , Ᾱ і В, Ᾱ і В̅ - незалежні події:

Р(А∩В̅) = Р(А) ∩ Р(В̅)

Р (А∩В̅) = Р(А) ∩ Р(В̅)=Р(А\(А∩В))=Р(А)-P(A)*P(B)=P(A)*(1-P(B))= P(A)*P(В̅ )

P(Ᾱ ∩ В̅ )=P(A U B)=1-P(A U B)=1-(P(A)+P(B)-P(A ∩ B))=1-P(A)-P(B)+

P(A)*P(B)=(1-P(B))-P(A)+ P(A)*P(B)=(1-P(B))-P(A)*(1-P(B))= (1-P(A))(1-

P(B))=P(Ᾱ)P(В̅ )

2Якщо А і В₁, А і В₂ – незалежні події , причому В₁∩ В₂ =порожня множина,

то незалежними є події А і В₁+В₂

P(A∩( В₁U В₂))=P((A∩В₁) U (A∩В₂))= P((A∩В₁) + (A∩В₂))= P(A)P(В₁) +

P(A)P(В₂)= P(A)(P(В₁) + P(В₂))= P(A)P(В₁ U В₂)

Def. події А1, А2,…..Аn називаються попарно незалежними, якщо Р(Аi) P(Аj) для i≠j

Def. події А1, А2,…..Аn називаються незалежними в сукупності, якщо незалежна кожна пара, кожна тріка, кожна четвірка, ….:

P(Ai1 *Ai2*… Air)=P(Ai1)*P(Ai2)*….*P(Air)

Попарна незалежність слідує з незалежності в сукупності. Незалежність в сукупності не слідує з попарної незалежності.