Питання:
Простір елементарних подій. Випадкові події, операції над ними.
Частотне та класичне означення ймовірності.
Імовірності в дискретних просторах елементарних подій.
Геометричне означення ймовірності. Задача Бюффона. Парадокс Бертрана.
Аксіоматичне означення ймовірності. Властивості ймовірностей.
Умовні ймовірності. Приклади.
Формула повної ймовірності та формула Байєса.
Незалежні події.
Дискретні випадкові події та їх характеристики.
Математичне сподівання випадкових величин. Властивості.
Дисперсій випадкових величин та його властивості.
Коефіцієнт кореляції випадкових величин.
Біномінальний, геометричний та пуассонівський росподіли. Їх характеристики.
Схема Бернулі. Локальна теорема Муавра-Лапласа.
Загальне поняття випадкової величини.
Функція розподілу. Щільність випадкових величин.
Рівномірний, показників та нормальний розподіли. Їх характеристики.
Функції від випадкових величин.
Багатовимірні розподіли.
Нерівність Чебишева.
Типи збіжності випадкових величин.
Генератриси, їх властивості.
Характеристичні функції та їх властивості.
Перша теорема Хелі.
Друга і третя теореми Хелі.
Теорема неперервності для характеристичних функцій.
Теорема Пуассона.
Закон великих чисел у формі Хінчина.
Закон великих чисел. Теореми Чебишева та Маркова.
Центральна гранична теорема для незалежних однаково розподілених випадкових величин.
Теорема Ляпунова. Умова Лінденберга.
Дискретні ланцюги Маркова. Матриця перехідних ймовірностей.
Класифікація станів дискретного ланцюга Маркова.
Рекурентні ланцюги Маркова.
Ергодична теорема для скінчених ланцюгів Маркова.
Поняття випадкового процесу. Скінченновимірні розподіли випадкових процесів.
Процеси з незалежними приростами.
Вінерів процес.
Пуассонівський процес.
Процеси відновлення. Функція відновлення.
Закон великих чисел для процесів відновлення.
Гіллясті процеси.
Ланцюги Маркова з неперервним часом.
Система диференціальних рівнянь Колмогорова для ланцюгів Маркова з нескінченним часом.
1. Простір елементарних подій. Випадкові події, операції над ними.
Випробування — реальний або мислений експеримент (виконуваний за певної незмінної сукупності умов), результати якого піддаються спостереженню.
Простір елементарних подій — множина можливих елементарних подій, кожною з яких може закінчитись випробування. Простір Ω може містити скінченну, зліченну або незліченну множину значень.
Ω
= 
– простір
елементарних подій;
- елементарний
наслідок;
Ω - може бути будь-якою структурою;
кількість
може бути будь-якою.
Випадкова подія — подія, яка в результаті випробування може відбутись, а може не відбутись.
Озн.: Будь-яка підмножина Ω називається випадковою подією.
Елементарні події — події, які не можна розкласти на простіші.
Операції над подіями:
1)
доповнення
(
)
2) об’єднання
(
)
;
;
- неможлива
подія;
;
;
;
;
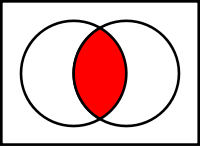
3)
перетин
(переріз)
(
)
4) різниця
(
)
;
;
;
;
;
;
;
Неможлива подія — подія, яка в даному випробуванні не може відбутись.
Достовірна подія — подія, яка в результаті випробування неодмінно відбудеться
Несумісними у випробуванні називаються події В і С, якщо відповідні їм множини елементарних подій не містять однакових елементів. Це означає, що коли одна з подій відбулась, друга подія відбутись не може.
Рівноможливими у випробуванні називаються події В і С, якщо є підстава вважати, що жодна з них не є об’єктивно більш можливою, ніж інша.
2. Частотне та класичне означення ймовірності
І.
В
просторі елементарних подій Ω зафіксуємо
довільну подію А. Експеримент повторюється
n разів( n – достатньо велике).
―
частота
події А( скільки разів А з'являлася в n
експериментах).
0
n;
Відносна
частота настання А в n експериментах:
.
Властивості
1)
2)
3)
Ǿ(
наприклад, парні і непарні числа)
.
Є вимога виконання властивості стійкості частот.
Теорема Бернуллі: При необмеженому збільшенні числа однорідних та незалежних дослідів відносна частота події А необмежено наближається до деякої сталої величини.
Означення Мізиса( частотне означення ймовірності)
Якщо
,
вона називається ймовірністю
події А,
а сама подія ― стохастично
стійкою.
Властивості
1)
2)
3)
Ǿ
Недоліки
означення: 1)
,
2) якщо
означення
статистичне оцінювання. Але аксіоматичним
означенням виступати не може.
ІІ. Нехай Ω ― скінчений дискретний простір.
,
n<+∞
(
ставимо у відповідність);
(
всі значення наслідків рівноможливі)
―
класичне
означення ймовірності(
відношення кількості точок події А до
загальної кількості точок)
Властивості
1)
2)
3)
,
при
=Ǿ
Для неможливої події P(Ǿ)=0 (m=0); Для вірогідної події P(Ω)=1 (m=n).