13.Логарифмічні частотні хар-ки.Побудова логарифмічних ха-к.

1.В log – координатах є можливість в більшості практичних випадках спрощено зображати амплітудні частотні хар-ки ломаними лініями. , .

2.В lg – масштабі амплітудна частотна ф-ція послідовно з’єднаних ланок = сумі амплітудних частотних ф-цій окремих ланок.

Амплітудна част. ха-ка побудована в lg-координатах у вигляді залежності від назив. логарифмічною амплітудною ха-ою(ЛАХ).

Залежність від назив логарифмічною фазовою ха-кою.

-логарифмічна амплітудна функція позначається :

-одиниці вимірювання -децибел(дБ)

-1 дБ=0,1 Б(Белл).Белл-це одиниця вимірювання десяткового lgкоеф. підсилення потужності сигналу.1 Б відповідає підсиленню в 10 раз;2 Б-в 100 раз

-так як потужність сигналу пропорційна квадрату амплітуди, а ,то підсилення в Беллах,що вираж. через відношення амплітуд= ,а підсилення в дБ =

-1 дБ відповідає зміні амплітуди в .

Асимптотична lg-ха-ка представляє собою сукупність відрізків прямих ліній з нахилом, що кратний 20 дБ на декаду.

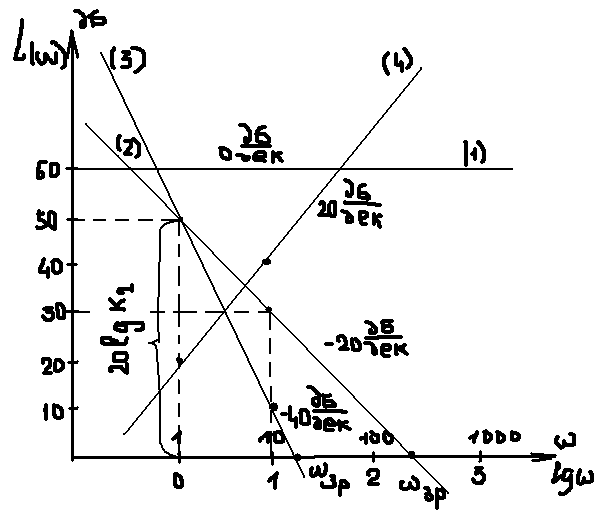
-частота зрізу

1. ; ,

2. ; ;

;

3. ;

; 4. ;

;

Ідеальна ланка-20дб/дек.

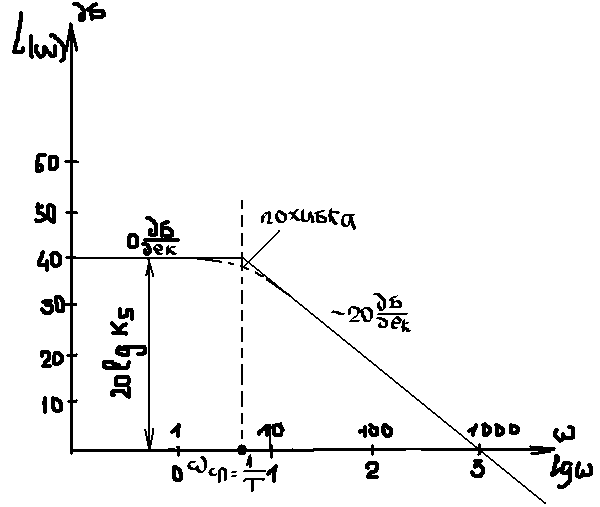
5. ; ; ;

35. Критерій стійкості Льєнара-Шипара (модифікований критерій Гурвіца)

Використовується для дослідження САК, які мають порядок n 5.

Якщо виконані необхідні умови стійкості:

>0, >0 , >0 , …, >0

То для стійкості САК необхідно і достатньо. Щоб серед визначників Гурвіца додатніми були всі визначники з парними індексами або всі визначники з непарними індексами, тобто

>0, >0 , >0 >0, >0, >0

Або

>0, >0 , …, >0, >0, >0, >0.

Приклад:

С-ма нестійка, так як один з коеф не є >0.

а) якщо всі визначники додатні, , то коли , то с-ма знаходиться на границі аперіодичної стійкості.

б) якщо , то с-ма знаходиться на границі коливної стійкості.

34. Критерій стійкості Гурвіца

>0

Складаємо визначник Гурвіца

Викреслюючи в головному визначнику Гурвіца діагональні мінори отримаємо визначник нижчих порядків:

;

Для того щоб САК була стійкою необхідно і достатньо, щоб всі визначники Гурвіца мали знаки однакові зі знаком першого коеф. характеристичного р-ня. Тобто при >0, всі визначники Гурвіца були додатні.

>0, >0, >0, >0, …, >0 .

Умови стійкості с-ми від 1 до 4 порядку:

1. n=1

>0, >0 – умова стійкості 1-го порядку

2. n=2

>0, >0 , >0 – умова стійкості 2-го порядку

3. n=3

>0, >0 , >0 , >0,

>0 - умова стійкості 3-го порядку

4. n=4

>0, >0 , >0 , >0, >0,

- умова стійкості 4 порядку

36. Критерій стійкості Михайлова

Підставляє в D( ), замість

де - дійсна частина отримана з членів , які мають парні степені .

- уявна частина, отримана з членів з непарними степенями .

Зобразимо на комплексній площині у вигляді АФЧХ змінюючи від 0 до ∞. Цей годограф назив. годографом Михайлова.

ω =0; ∞.

Цей годограф починається на дійсній додатній півосі .

Критерій Михайлова:

С-ма стійка, якщо годограф Михайлова починається на дійсній додатній півосі огинає проти годинникової стрілки початок координат проходить послідовно комплексну площину.

- порядок с-ми або характеристичне р-я.

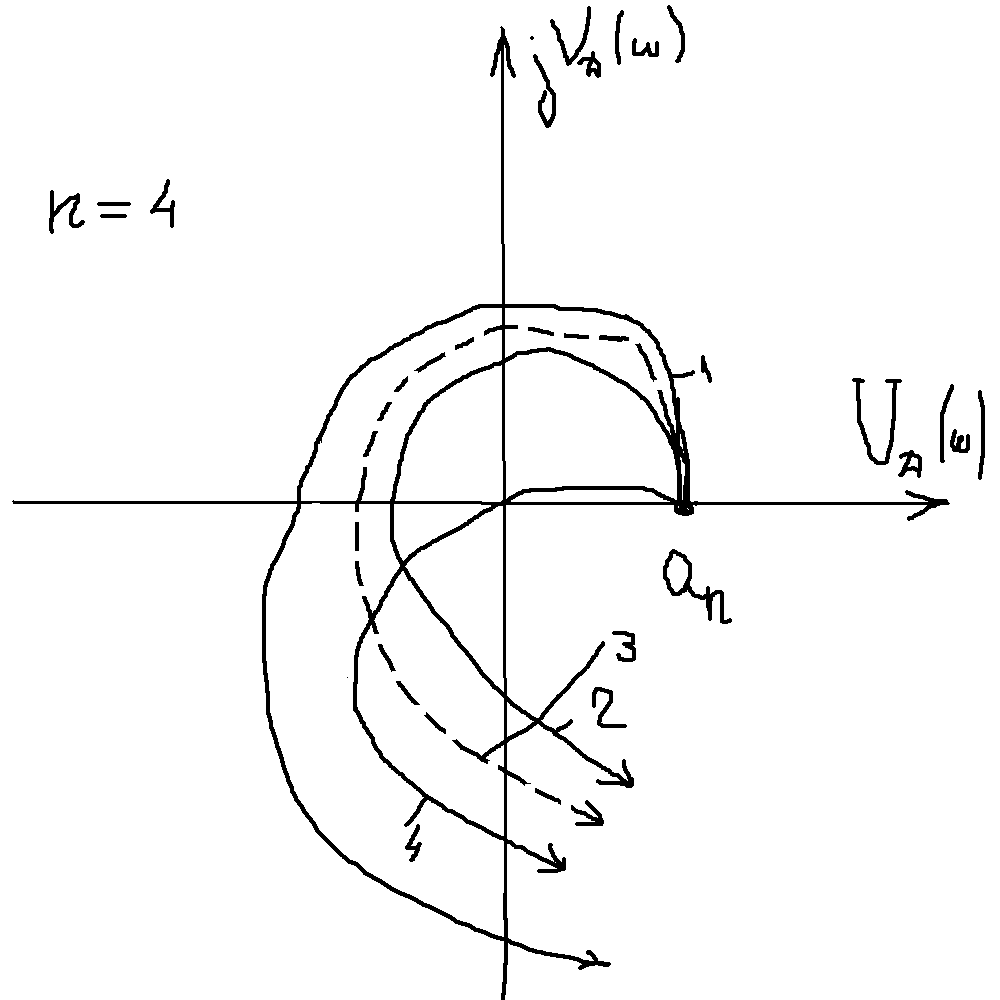
1-с-ма стійка

2,3-с-ма нестійка

4 с-ма знах на границі стійкості

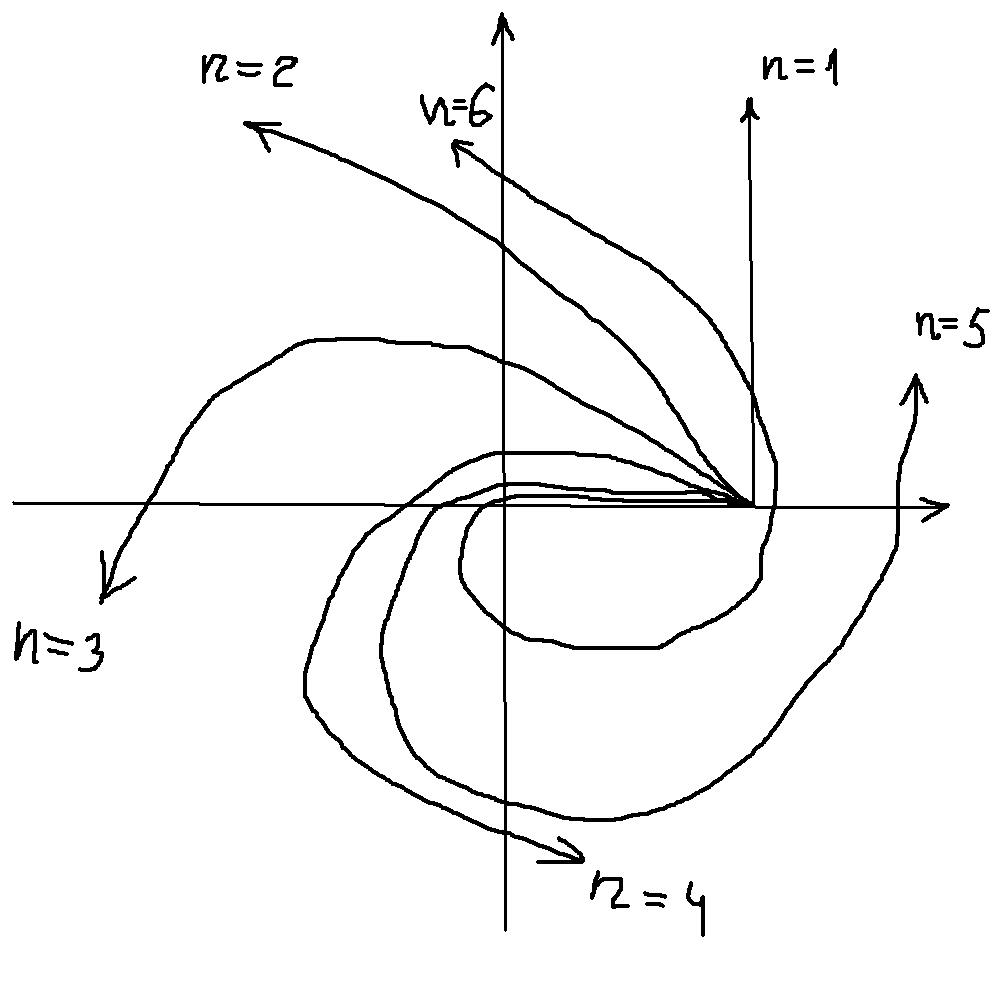
Для побудови годографа спочатку находять точки його перетину з координатними осями. Для цього визнач з р-ня значення частот, які відпов точкам перетину годографа з уявною віссю, і підставляємо ці значення у вираз і визнач відповідні ординати.

Аналогічно визначаємо точки перетину з дійсною віссю, прирівнюючи до =0.

Дійсну і уявну ф-цію Михайлова і можна представити графічно у вигляді кривих.

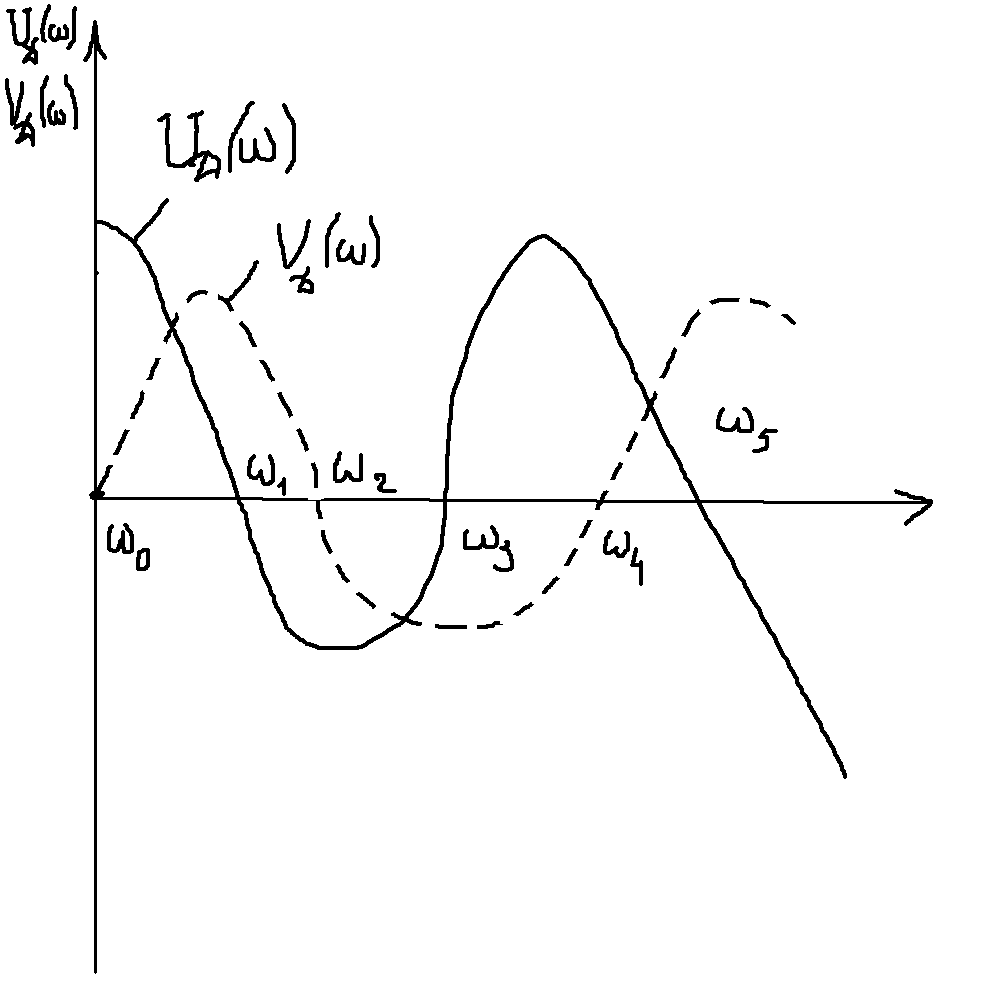
Якщо значення кривих корені р-ня .

, корені р-ня =0, при цьому < < <…

< < <…,

То для стійкості с-ми необхідно щоб < < < < < <….

Тоді критерій Михайлова можна сформулювати так:

С-ма САК буде стійка тоді і тільки тоді, коли дійсна і уявна ф-ці Михайлова = 0 мають всі дійсні корені, що чергуються, до того ж загальна к-сть цих коренів = порядку і при =0 задається умова >0, >0.