28. Определение производной функции в точке. Геометрический смысл производной. Правила дифференцирования.

Пусть f – функция с областью определения D(f), x₀ – внутренняя точка множества D(f) // это значит существует (а, в)>0, включающийся в D(f), :, x₀ принадлежит (а, в)//.

Опр. 1 Предел 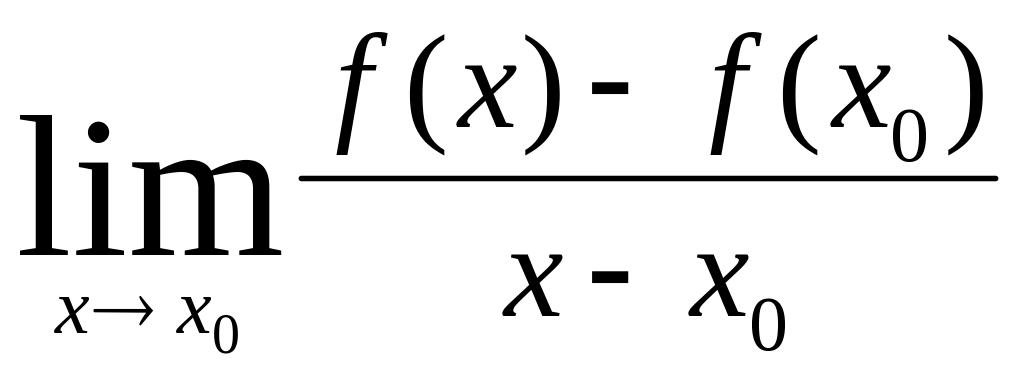, в том случае когда он существует, называется производной функции f в точке x₀ и обозначается через  . Функция f, имеющая производную в точке x₀, называется дифференцируемой в точке x₀.

Геометрический смысл производной: производная функции f в точке x₀ равна тангенсу угла наклона касательной к графику функции f в точке M₀ с координатами (x₀, f(x₀)):

∆M₀CM VC=f(x)-f(x₀) CM₀=x-x₀

MC/CM₀=tg∟MM₀C=tg α_x => f’(x₀)=tg(lim α_x) x→x₀ => f’(x₀)= tgα

Уравнение касательной: y-f(x₀)=f’(x₀)(x-x₀)

Для выяснения механического смысла производной представим, что некоторая материальная точка движется прямолинейно по закону , указывающему величину пройденного пути S к моменту времени t. Ясно, что за промежуток времени от x₀ до x, x>x₀, материальная точка прошла путь . Так как это произошло за время , то можно вычислить среднюю скорость движения материальной точки на этом отрезке пути: (1).

Интуитивно ясно, что величина V_ср тем точнее характеризует мгновенную скорость движения материальной точки в момент времени t=t₀ /обозначим ее через V(t₀)/, чем меньше t отличается от t₀. Вот почему в механике принято считать, что . Однако, в силу равенства (1), тогда . То производная функции S=S(t) в точке t₀ – это мгновенная скорость движения материальной точки в момент времени t=t₀.

Заметим, что условие непрерывности функции f в точке х₀ не влечет ее дифференцируемости в точке х₀(пр. y=|x| в точке х₀).

Лемма. Если функция f дифференцируема в точке х₀, то она и непрерывна в этой точке х₀.

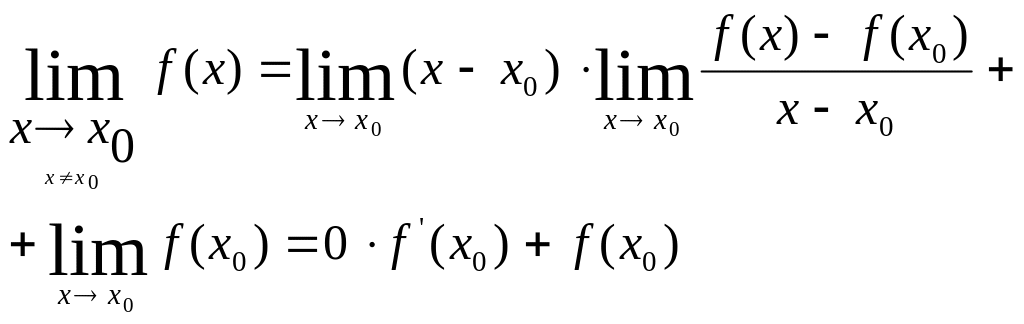Док-во: Т.к. при х≠х₀ еханике принято считать, что точки в момент материальной точки на это материальная точка движется прямолинейно по закону 0000 то по св-вам предела функции имеем Т.1. Пусть функции f и g дифференцируемы в точке х₀ и пусть х₀ – внутренняя точка мн-ва D(f)∩D(g). Тогда в точке х₀ дифференцируемы функции f+g, f-g, f*g, а при g(x₀)≠0 и функция f/g. При этом выполняются следующие равенства: 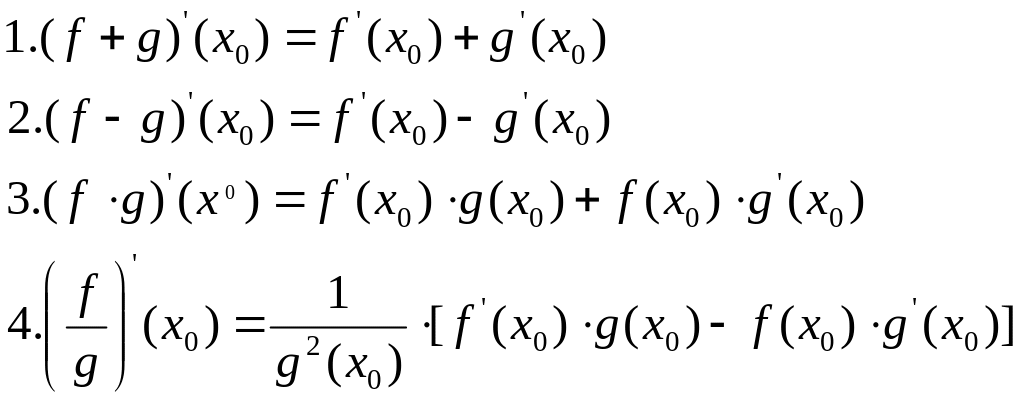Док-ва во всех 4 случаях сходны. Остановимся подробнее на примере функции f*g. Док-во: Чтобы док-ть существование (f*g)^’(x₀) и вычислить ее заметим, что. .

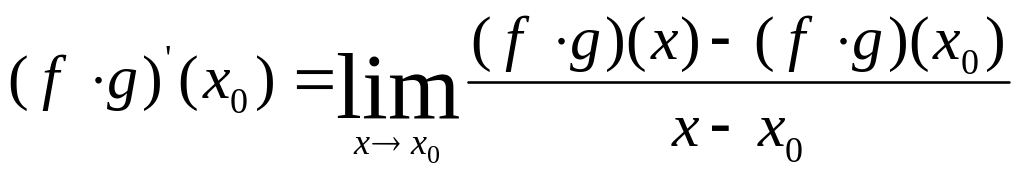D(fg)=D(f)∩D(g)

X₀- внутренняя точка D(f)=> δ₁ – окрестность точки х₀:

X₀ – внутренняя точка D(g)=> δ₂ – окрестность точки х₀:

Рассмотрим δ=min{δ₁; δ₂}

(x₀- δ;x₀+ δ)c(x₀-δ₁;x₀+ δ)cD(f)|

(x₀- δ;x₀+ δ)c(x₀- δ;x₀+ δ)cD(g)| =>(x₀- δ;x₀+ δ)cD(f)∩D(g)

Представим выражение под знаком предела в удобной форме:

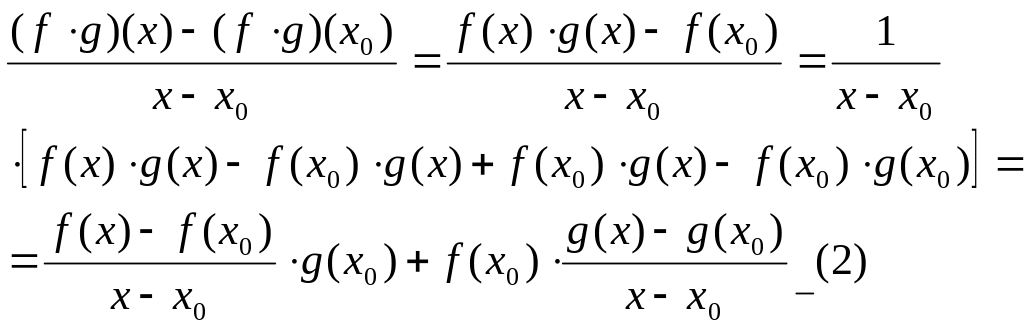Т.к. при х→х₀, в силу лемме, g(x)→g(x₀), а из дифференцируемости функций f и g в точке х₀, следует , то по Т.( Если существуют конечные пределы функций f и g в точке х₀, причем х₀ – точка прикосновения мн-ва D(f)∩D(g), то в ней существуют пределы функций f+g, f-g, f*g) существует предел выражения (2), причем он равен именно правой части доказываемой формулы 3.

//Для док-ва 4.:

По условию по Лемме: y=g(x) непрерывна в точке х₀ т.е.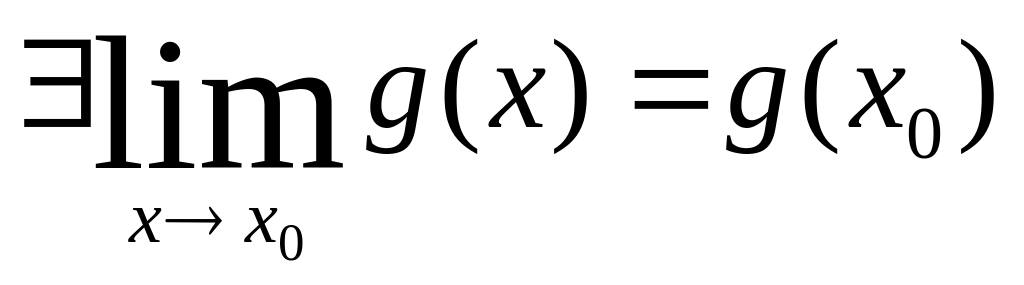

Рассмотрим g(x₀)>0=>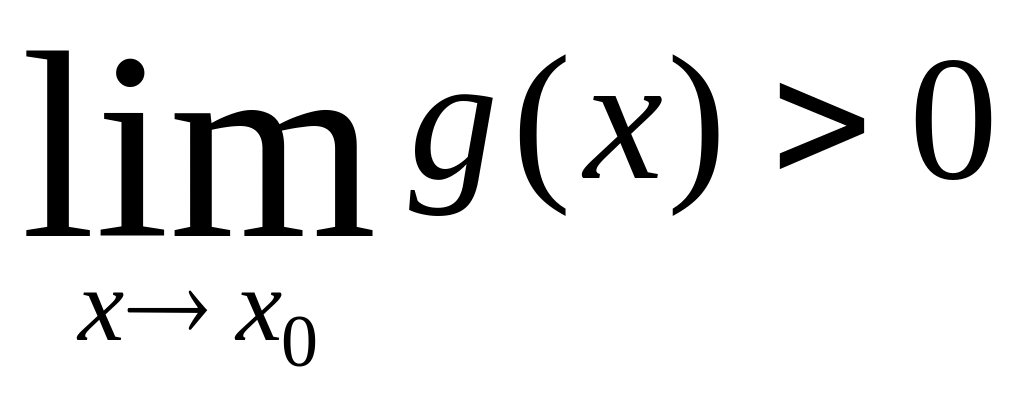 по Т. о локальном сохранении знака(если предел в точке >0, то существует окрестность этой точки, во всех точках которой знак тоже положительный)=>

δ=min{δ₁,δ₂,δ₃}

(x₀-δ;x₀+δ)c(D(f)∩D(g))\{x:g(x)=0}//

Т.2. Пусть функция f дифференцирована в т.x₀, причем f(x₀)≠0. Пусть Т=f(x₀) и на некотором интервале, содержащем Т определена обратная функция F(х), непрерывная в т. Т. Тогда эта функция дифференцирована в т. Т, причем F'(Т)=1/f(x₀).

Т.3. Пусть функция f дифференцирована в т. x₀ и пусть в некотором интервале, содержащем т. x₀ определена следующая функция

S(x)=g◦f(x)=g(f(х)). Обозначим Т=f(x₀). Если внешняя функция g дифференцирована в т.Т, то сложная функция S(х) дифференцирована в т. x₀, причем S^’(x₀)=g^’(T)*f ^’(x₀)=

=g^’(f(x₀))*f ^’(x₀), т.е. производная композиции равна произведению производных, составляющих эту функцию.