Министерство Науки и Образования Российской Федерации

Санкт-Петербургский государственный электротехнический университет

Кафедра МОЭВМ

Отчет

по лабораторной работе №6

Вариант 19.

по дисциплине

«Цифровая обработка сигналов»

Выполнил: Эмман П.А.

Группа: 3351

Факультет КТИ.

Проверил: Жукова Н.

Санкт-Петербург.

2007г.

1. Цель работы

Изучение методов использования алгоритма быстрого преобразования Фурье (БПФ) для решения задач оценки спектральных характеристик различных сигналов с помощью ЭВМ, а также исследование свойств дискретного преобразования Фурье, непосредственно влияющих на качество получаемых спектральных оценок.

2.1. Изучение частотной характеристики БПФ

2.1.1. Задание

Задать параметры:

n=1024 - длина реализации БПФ (N=10, f_дискретизации будет равно 1024 Гц).

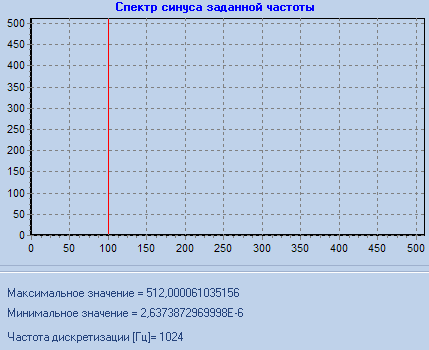
f_sin=100 Гц

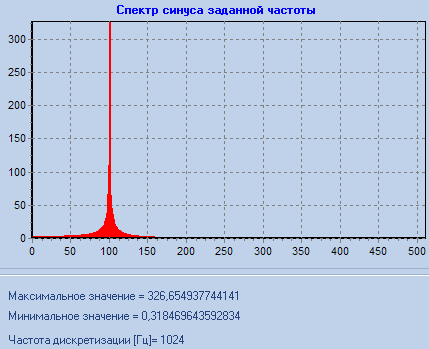
f_sin=100,5 Гц

Сравнить результаты,

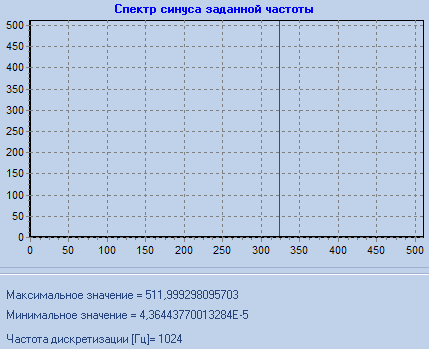
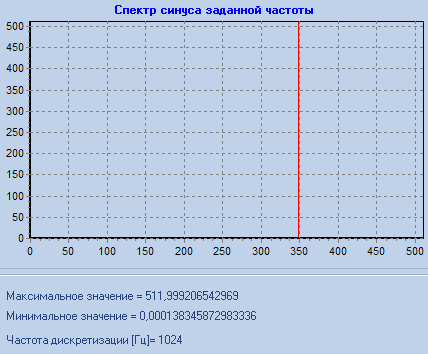
f_sin= 700,1100,1700,2100

Объяснить полученные результаты.

2.1.2. Выполнение

f_sin = 100	f_sin = 100,5
f_sin = 700	f_sin = 1100

f_sin = 1700	f_sin = 2100

2.1.3. Вывод

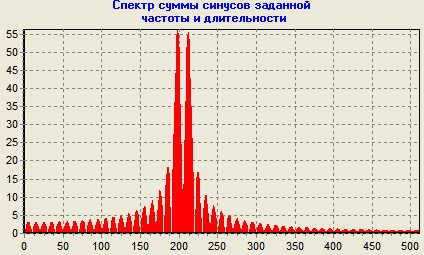
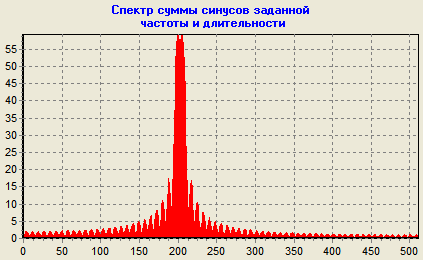
1) При f_sin = 100,5 наблюдаем «растекание спектра». Оно обусловлено некратностью частоты синуса шагу частоты дискретизации. При этом на спектре вместо единственного истинного значения амплитуды виден набор значений с меньшей амплитудой, максимальное из которых будет зависеть от соотношения частоты сигнала и шага частоты дискретизации.

2) В остальных случаях не выполняются условия теоремы Котельникова. Из-за этого происходит подмена частот. Согласно соотношениям:

=>

=> f₀^’’= f₀

2.2. Изучение разрешающей способности БПФ по частоте

2.2.1. Задание

Задать параметры:

N=1024 - длина реализации БПФ (n=10),

f1=300, f2=310 проверить разрешение по частоте.

Подобрать длину реализации сигнала, при которой сохраняется разрешение. Объяснить результаты. Надо учесть, что при моделировании для заданного N длина реализации сигнала уменьшается путем замены части отсчетов нулями. Реальное разрешение по частоте равно при этом 1/T, где T- длина сигнала.

То же проделать для частот 200; 210 Гц и 200; 205 Гц.

2.2.2. Выполнение

f1 = 300 f2 = 310
N = 70	N = 103
f1 = 200 f2 = 210

N = 70	N = 103
f1 = 200 f2 = 205
N = 128	N = 133

2.2.3. Вывод

Для распознавания частот синусов как различных необходима длина реализации синуса:

N_DFT / N_sin = d

Для случаев 1) и 2) d = 10, N_sin = 1024 / 10 = 102,4

Для случая 3) d = 5, N_sin = 1024 / 5 = 204,8

2.3. Применение окон для спектрального анализа

2.3.1. Задание

Задать параметры:

1. n=1024 - длина реализации БПФ (N=10)

2. M=20 - ширина окна.

3. Необходимо учесть, что при таком выборе М и N 1 бин будет соответствовать 1024/20 = 50 точек (здесь использована интерполяция для расширения графического изображения окна).

4. Нажать кнопку "Без синуса"

5. Выбрать тип окна, нажать кнопку "Выполнить БПФ"

6. Включить "шкала логарифмическая"

7. Включить "пропускать через окно" (При включенной кнопке "пропускать через окно" программа работает с заданным окном, при выключении кнопки - можно рассчитать спектр синусоидального сигнала без окна.)

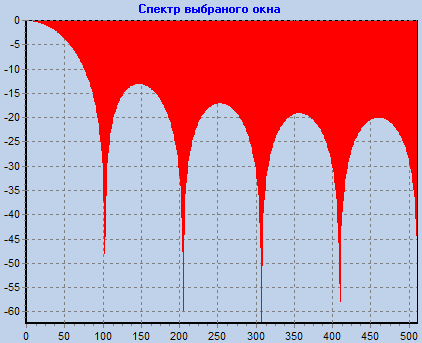
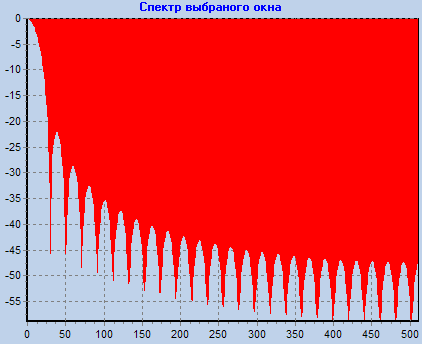
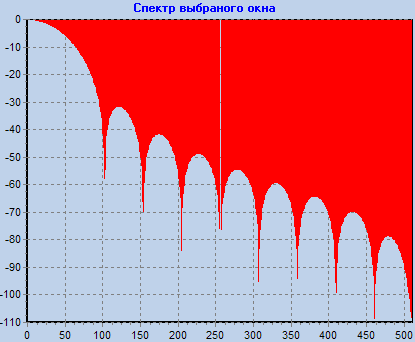
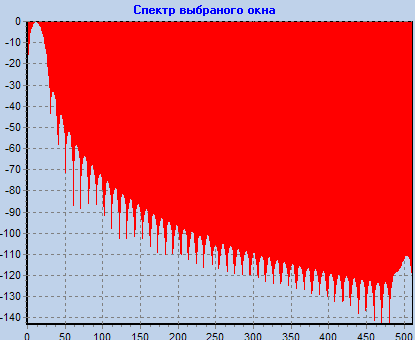
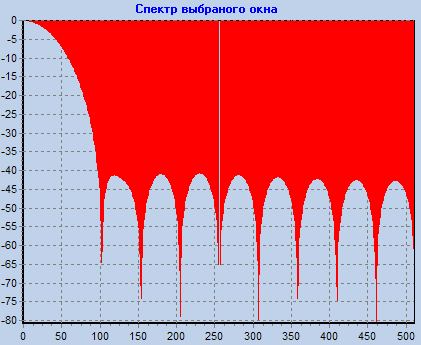
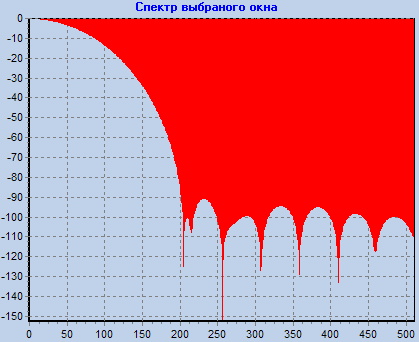
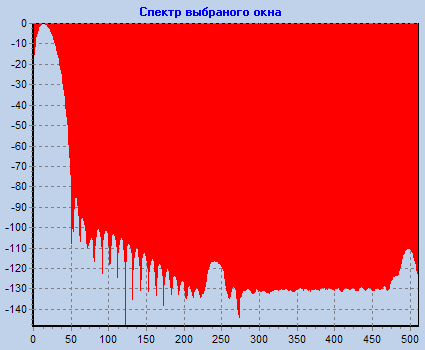
8. Просмотреть частотные характеристики различных окон. Определить ширину главного лепестка и скорость спада боковых лепестков (для первых пяти лепестков) для всех окон.

9. Провести сравнение спектра синусоидального сигнала при использовании БПФ без окна (при этом выключается "пропускать через окно") и с использованием всех окон (установить "с синусом", "частота синуса", n=10 , ширина окна M=100)

2.3.2. Выполнение

Вид	Без синуса	С синусом n = 10
Прямоугольное M=20
Треугольное M=20
Хеннинга M=20
Хемминга M=20
Блекмана-Харриса M=20
Синус n = 10 Без окна

2.3.3. Вывод

Получены параметры окон:

Окно	Ширина гл. лепестка,	Скорость спада лепестков, дБ/окт
	точек	1	2	3	4
Прямоугольное	50	-6,26	-2,08	-1,62	-1,05
Треугольное	100	-5,43	-1,77	-0,89	-0,45
Хеннинга	100	-13,46	-5,71	-3,63	-2,66
Хемминга	100	-17,87	0,5	0	-0,53
Блекмана-Харрриса	200	-38,96	6,73	-5,14	3,28

Наиболее эффективно боковые лепестки подавляются окном Блекмана-Харриса.

2.4. Влияние накопления на характеристики спектрального анализа

2.4.1. Задание

1) Количество точек реализации n = 1024 (частота дискретизации 1024 Гц).

2) Мощность шума здесь - С.К.О (sigma)

3) Амплитуда полезного сигнала (SIN)-A

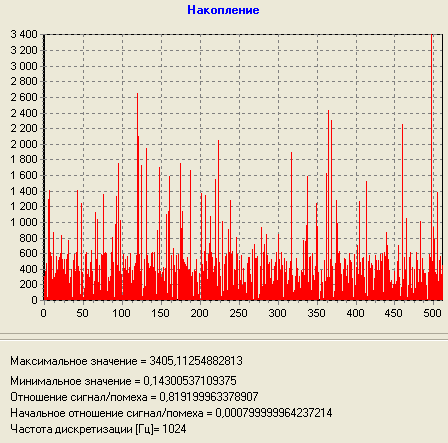
4) Отношение сигнал/помеха q=A*A/(2*sigma*sigma) вычисляется в программе. Это отношение сигнал/помеха во входном сигнале. После спектрального анализа отношение в каждом фильтре БПФ становится q1=q*N. Если сделать M накоплений по времени, то отношение q2=q1*(M)^0,5. Сигнал на спектре визуально можно обнаружить при отношении сигнал/помеха не менее 8-10.

5) Рассмотреть вариант:

sigma=10, 25, 50

A=1

f=150 Гц

6) Определить теоретически и экспериментально необходимое количество накоплений, чтобы надежно выделить гармонический сигнал.

2.4.2. Выполнение

Рассчитаем теоретическое количество накоплений:

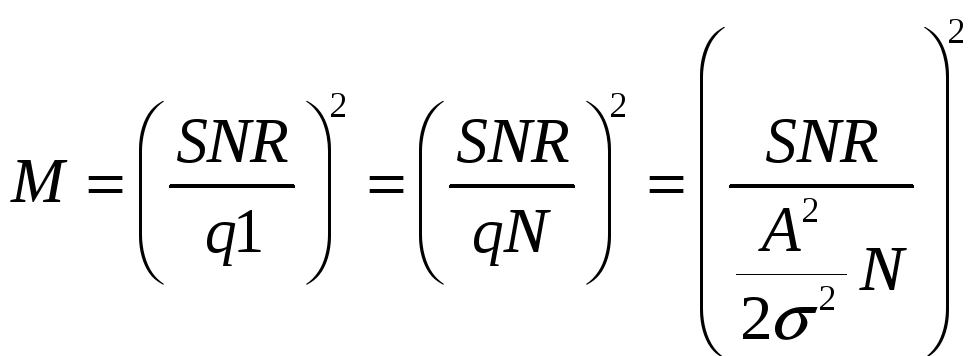
Параметры	Результат
sigma = 10	Теоретически: SNR = 10 при M = 4 Экспериментально: SNR = 10 при M = 4
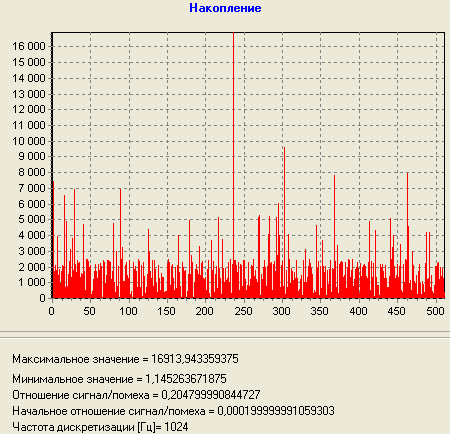
sigma = 25	Теоретически: SNR = 10 при M = 4 Экспериментально: SNR = 10 при M = 149
sigma = 50	Теоретически: SNR = 10 при M = 2384 Экспериментально: SNR = 10 при M = 2400

2.4.3. Вывод

Значения параметра усреднения по времени, полученные экспериментально, близки к полученным теоретически. При этом визуальное обнаружение сигнала на спектре наступало раньше, чем достигалось SNR=8-10.

11