
- •1. Типовые преобразования сообщений 3
- •1. Типовые преобразования сообщений
- •1.1. Преобразование вида представления сообщений.
- •1.2. Сжатие объема сообщений.
- •1.3. Повышение помехоустойчивости.
- •1.4. Повышение верности оценок и целевая обработка.
- •2. Дельта - модуляция
- •2.1. Общие замечания.
- •2.2. Выбор основных характеристик дельта-модуляции.
- •2.3 Повышение помехоустойчивости при дельта-модуляции.
- •3. Базовые алгоритмы дельта - мод ляции
- •3.1.Линейная дельта-модуляция.
- •3.2.Троичная дельта-модуляция.
- •3.5. Алгоритм Синклера.
- •3.4. Дельта-модуляция с компрессированием.
- •4. Работа с программой
- •4.1. Описание интерфейса
- •4.2. Инструкция по работе с программой
- •4.3. Результаты прогонки тестового примера
2.2. Выбор основных характеристик дельта-модуляции.
При
дельта представлении возникают ошибки
двух видов: квантования (![]() )
и перегрузки (
)
и перегрузки (![]() )
(Рис. 6). Максимальная ошибка квантования
не превышает шага квантования, если
перегрузки по крутизне отсутствуют.
Ошибки перегрузки возникают, если
крутизна сообщения превышает максимально
допустимую при дельта- представлениях.
Последняя определяется произведением
величины шага квантования
)
(Рис. 6). Максимальная ошибка квантования
не превышает шага квантования, если
перегрузки по крутизне отсутствуют.
Ошибки перегрузки возникают, если
крутизна сообщения превышает максимально
допустимую при дельта- представлениях.
Последняя определяется произведением
величины шага квантования![]() на
частоту опроса
на
частоту опроса![]() .
Поэтому, для того чтобы система не
перегружалась. должно удовлетворяться
следующее условие:
.
Поэтому, для того чтобы система не
перегружалась. должно удовлетворяться
следующее условие:
![]() (2.8)
(2.8)
где
![]() -
модуль первой производной сообщения
по времени.
-
модуль первой производной сообщения
по времени.
Если сообщение описывается недифференцируемой функцией или значения производных априори неизвестны, но известно, что сообщение удовлетворяет условию Липшица (6),т.е.
![]() (2.9)
(2.9)
то должно удовлетворяться следующее условие:
![]() (2.10)
(2.10)
Поскольку
шаг квантования
![]() выбирается исходя из заданной погрешности
квантования, частота опроса при дельта-
представлении должна выбираться из
условия
выбирается исходя из заданной погрешности
квантования, частота опроса при дельта-
представлении должна выбираться из
условия
![]() (2.11)
(2.11)
или
![]() (2.12)
(2.12)
Для нормального стационарного стохастического сообщения при доверительной вероятности Рj = 0.99
условие (2.8) можно записать в следующем виде (4):
![]() (2.13)
(2.13)
где
![]() - дисперсия (мощность)
первой производной сообщения.
- дисперсия (мощность)
первой производной сообщения.
Например, для сообщения с ограниченным спектром и корреляционной функцией вида
![]() (2.14)
(2.14)
дисперсия 1-й производной
![]() (2.15)
Тогда
при шкале сообщения
(2.15)
Тогда
при шкале сообщения
![]() (2.16)
(2.16)
и шаге квантования
![]() (2.17)
(2.17)
требуемая частота опроса будет:
![]() (2.18)
(2.18)
2.3 Повышение помехоустойчивости при дельта-модуляции.
Дельта-
представления имеют тот недостаток,
что в каналах с шумами погрешности в
оценке координат на приемной стороне
накапливаются. Если на приемной стороне
вместо каждой координаты
![]() принимается координата
принимается координата![]() и если погрешность
и если погрешность![]() в разных координатах(i=1,2...)
есть реализации некоррелированных
случайных величин с математическим
ожиданием равным нулю и одинаковой
дисперсией
в разных координатах(i=1,2...)
есть реализации некоррелированных
случайных величин с математическим
ожиданием равным нулю и одинаковой
дисперсией
![]() (6),
то
через время
(6),
то
через время
![]() (
(![]() -
период опроса)
дисперсия
погрешности в оценке сообщения возрастает
до (2)
-
период опроса)
дисперсия
погрешности в оценке сообщения возрастает
до (2)
![]() (2.19)
(2.19)
Поэтому
для уменьшения влияния эффекта накопления
погрешностей длительность интервала
представления сообщения
![]() (n
-
количество переданных координат) должна
быть не очень большой,
т.е.
опорная координата
(n
-
количество переданных координат) должна
быть не очень большой,
т.е.
опорная координата
![]() должна повторяться согласно (2.19) через
должна повторяться согласно (2.19) через
![]() (2.20)
(2.20)
координат,
где
![]() - допустимая погрешность в оценке
сообщения точек опроса. Последнее влечет
за собой увеличение объема передаваемых
сообщений, так как объем опорных координат
может быть значителен (2.5).
- допустимая погрешность в оценке
сообщения точек опроса. Последнее влечет
за собой увеличение объема передаваемых
сообщений, так как объем опорных координат
может быть значителен (2.5).
3. Базовые алгоритмы дельта - мод ляции
Рассмотрим математическое представление алгоритмов для важнейших типов ДМ.
3.1.Линейная дельта-модуляция.
Все сказанное выше относительно базовых принципов ДМ можно почти без изменений отнести к описанию ЛДМ. Алгоритм описывается соотношением (2.1).
Подробное исследование ЛДМ было проведено Аббатом (8),в частности он приводит зависимость отношения сигнал/шум от нормированного шага
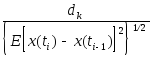 (3.1)
(3.1)
и
![]() (3.2)
(3.2)
где
![]() -частота
дискретизации, а
-частота
дискретизации, а![]() -частота
Найквиста (7).
-частота
Найквиста (7).
Из
(Рис. 7) видно, что для данного значения
![]() отношение сигнал/шум достигает максимума
при некотором
отношение сигнал/шум достигает максимума
при некотором![]() .
Значения
.
Значения
![]() ,
лежащие
левее этого максимума, соответствуют
перегрузке по крутизне.
,
лежащие
левее этого максимума, соответствуют
перегрузке по крутизне.
Кроме того, Аббат (8) вывел эмпирическую формулу для оптимального шага квантования аналогично (2.8):
![]() (3.3)
(3.3)
Как
оказалось, отношение сигнал/шум в большой
степени зависит от уровня входного
сигнала (8), т.е. согласно (9) для получения
качества восстановления,
сравнимого
с качеством,
достигаемым
в ИКМ, требуется значительно больная
частота дискретизации. Кроме того,
отсутствие сигнала порождает для такого
алгоритма ошибку с размахом
![]() , называемую шумом дробления.
, называемую шумом дробления.
Поэтому дальнейшее развитие ЛДМ связано с одной стороны с введением адаптивных методов квантования, а с другой - с использованием многоуровневой ДМ. Обратимся сначала к троичной дельта-модуляции.
