23,4 Долл/кг.
Таким образом, применение формулы расчета средней арифметической взвешенной позволило учесть влияние структуру исходных данных.
Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах.
В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот.
Рассмотрим пример вычисления средней арифметической в дискретном ряду:
Цена тонны условного товара, долл. Xi |
Частота (количество тонн), шт. fi |
Произведение вариант на веса (частоты) Xi*fi |
1200 |
1 |
1200 |
1300 |
2 |
2600 |
1400 |
2 |
2800 |
1500 |
5 |
7500 |
1600 |
3 |
4800 |
1650 |
2 |
3300 |
1700 |
1 |
1700 |
1750 |
1 |
1750 |
1800 |
1 |
1800 |
1950 |
1 |
1950 |
2000 |
1 |
2000 |
Итого: |
20 |
31400 |
В интервальных рядах значение признака задано, как известно, в виде интервалов, поэтому, прежде чем рассчитывать среднюю арифметическую, нужно перейти от интервального ряда к дискретному.
В качестве вариантов Xi используется середина соответствующих интервалов. Они определяются как полусумма нижней и верхней границ.
Если у интервала отсутствует нижняя граница, то его середина определяется как разность между верхней границей и половиной величины следующих интервалов. При отсутствии верхних границ, середина интервала определяется как сумма нижней границы и половины величины предыдущего интервала. После перехода к дискретному ряду дальнейшие вычисления происходят по методике рассмотренной выше.
Средней гармонической величиной называют величину, рассчитанную из обратных значений варьирующего признака. Она применяется и как обобщающая характеристика относительных величин.
Также как и средняя арифметическая, средняя гармоническая может быть простой и взвешенной.
Средняя гармоническая простая:
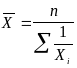(10.3)
Средняя гармоническая взвешенная:
,
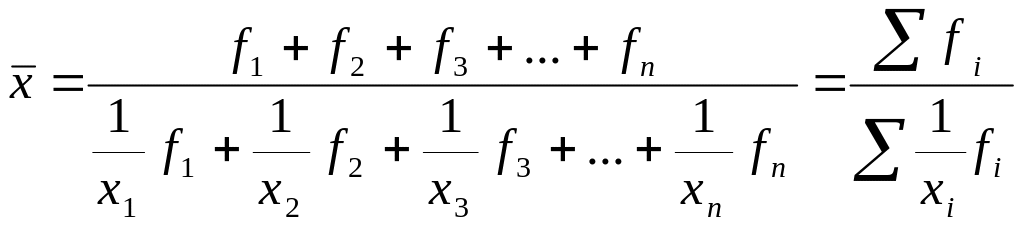(10.4)
где fi - частоты;
Xi - индивидуальные значения.
В приведенном ниже примере необходимо найти, сколько процентов в среднем по стране составил импорт по некоторой товарной группе за 2001 год по сравнению с 2000 годом. Для этой цели можно использовать среднюю гармоническую. В качестве значений признака будут выступать проценты, а в качестве частот – объемы импорта за 2001 год.
Таблица 10.2
|
1 страна |
2 страна |
3 страна |
4 страна |
Объем импорта за 2001г, тыс.дол. |
2450 |
3000 |
1400 |
2160 |
В % к импорту за 2000г |
70 |
60 |
70 |
90 |
.
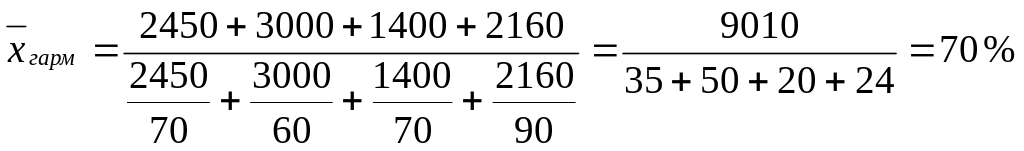Средней геометрической принято именовать величину, исчисляемую как корень n–ной степени из произведения n отдельных вариантов признака.
Она также обычно используется для характеристики относительных величин и рассчитывается по формуле:
,
(10.5)
Пример. Темпы роста в период с 1998-2001 гг. составили соответственно 50%; 40%; 60%; 20%. Определить средний темп роста. Воспользуемся формулой 10.5. Средний темп роста составит
39%.
В случаях, когда некоторые либо все варианты (коэффициенты темпов роста, например) относятся к периодам, не одинаковым по продолжительности, средний коэффициент роста исчисляется по формуле средней геометрической взвешенной:
, (10.6)
где х - варианты;
fi - веса;
-
сумма весов.
Допустим, что коэффициент роста физического объема внешней торговли за периоды:
1994-1998 гг. - 115 %
1998-2001 гг. – 104,7%
2001-2004 гг. прогноз - 101%
Средний темп роста, рассчитанный по формуле 10.6 составит 108%.
При расчете средних величин необходимо помнить о том, что всякие промежуточные вычисления должны приводить как в числителе, так и в знаменателе к имеющим экономический смысл показателям.