7. Модель Леонтьева межотраслевого баланса
Задача 7.
Некоторая экономическая система задана
матрицей прямых затрат
,
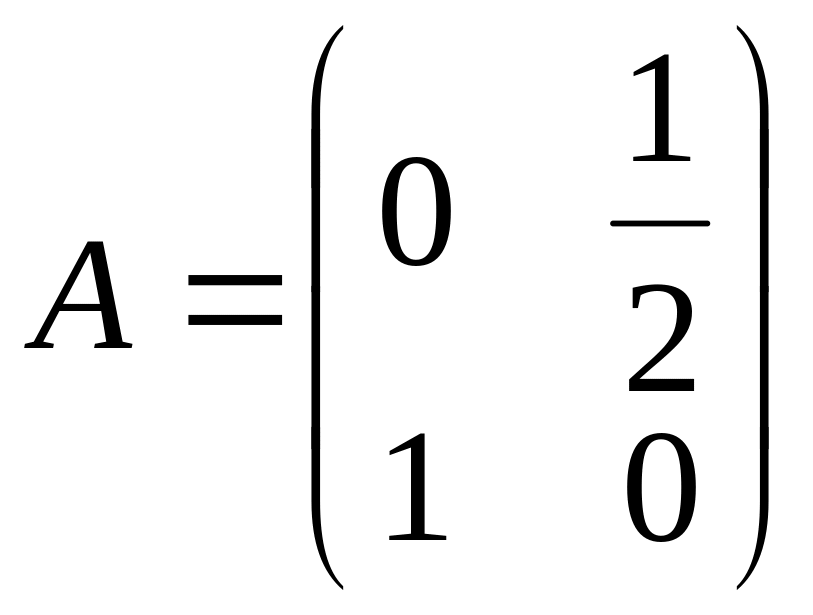вектором прямых потребностей в труде
и вектором конечного потребления
.
Требуется:
1) Проверить
продуктивность модели Леонтьева
;
2) Вычислить косвенные потребности во всех продуктах, включая труд, для чистого выпуска единицы каждого продукта;
3) Найти нормализованный вектор равновесных цен и соответствующую ему ставку заработной платы;
4) Определить
суммарный выпуск каждой отрасли и
суммарную потребность в труде для
производства ассортиментного набора
продуктов
.
Решение.
Развернутое изложение модели Леонтьева содержится в монографиях [2], [7]. Краткое описание этой модели приведено в методической разработке [8], терминологию и обозначения которую мы будем использовать в дальнейшем.
Матричная форма
записи модели Леонтьева (для рассматриваемого
в данной задаче случая двухотраслевой
экономики) имеет вид:
,
где
- вектор (столбец) валового выпуска
продуктов,
- заданный вектор (столбец) конечного
потребления продуктов,
- заданная матрица прямых затрат
продуктов.
1) Для проверки продуктивности модели Леонтьева применим следующий критерий продуктивности:
модель Леонтьева
продуктивна тогда и только тогда, когда
выполнено условие
;
где
- наибольшее положительное собственное
значение матрицы прямых затрат
.
Найдем собственные
значения матрицы
,
т.е. корни характеристического уравнения
:
,
,
,
.
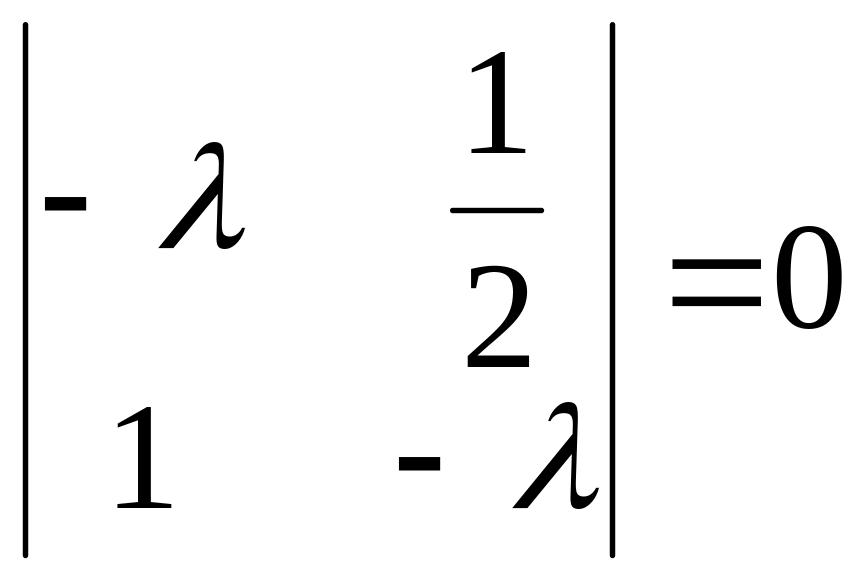Таким образом
,
и условие
выполнено, т.е. модель Леонтьева является
продуктивной.
2) Для нахождения
матрицы косвенных затрат продуктов
применим формулу
,
где
- так называемая матрица полных затрат
продуктов.
Последовательно находим:
;
,
,
,
,
;
;
.
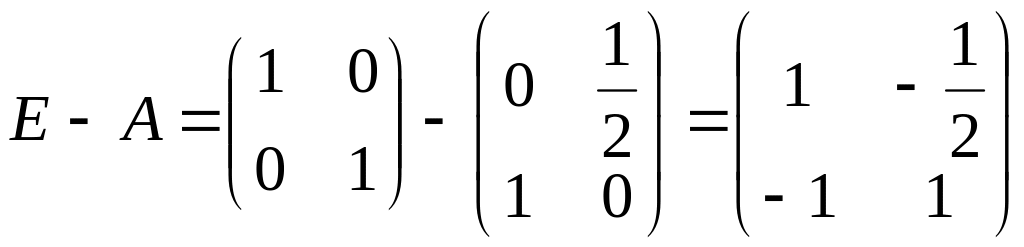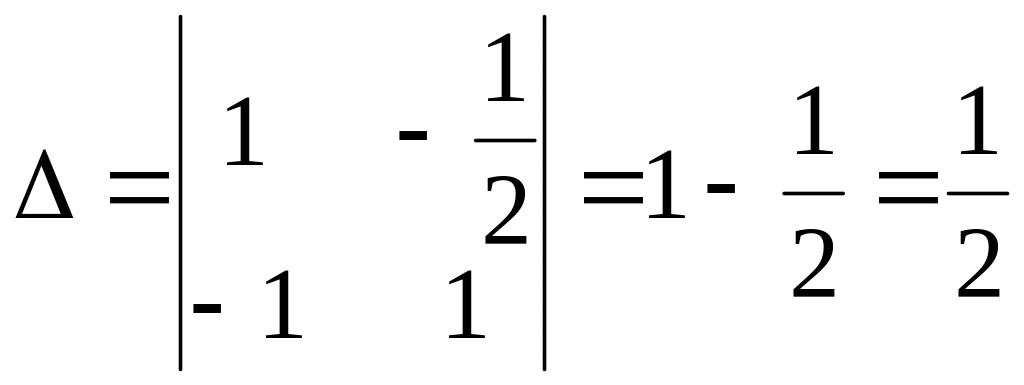В результате получаем:
(косвенные затраты
1-го продукта для чистого выпуска единицы
1-го конечного продукта);
(косвенные затраты
1-го продукта для чистого выпуска единицы
2-го конечного продукта);
(косвенные затраты
2-го продукта для чистого выпуска единицы
1-го конечного продукта);
(косвенные затраты
2-го продукта для чистого выпуска единицы
2-го конечного продукта).
Далее найдем вектор
косвенных потребностей в труде
для чистого выпуска единицы соответствующего
конечного продукта. Применим формулу
,
где
- вектор (строка) полных потребностей в
труде.
Последовательно находим:
,
.
Следовательно,
(косвенные затраты
труда для чистого выпуска единицы 1-го
конечного продукта);
(косвенные затраты
труда для чистого выпуска единицы 2-го
конечного продукта);
3) Для нахождения
нормализованного вектора равновесных
цен на продукты
и соответствующей ему ставки заработной
платы
применим следующие формулы:
,
,
,
где
,
координаты вектора полных потребностей
в труде.
Получаем:
;
,
.
4) Вектор валового выпуска продуктов найдем по формуле
:
.
Таким образом,
(количество
продукта, выпускаемое 1-ой отраслью);
(количество
продукта, выпускаемое 2-ой отраслью).
Суммарная потребность
в труде для производства заданного
конечного продукта
(трудоемкость производства) выражается
скалярной величиной
.
Рекомендуемая литература
1. Малыхин В.И. Финансовая математика: Учеб. пособие для вузов. – 2-е изд., перераб и доп. – М.: ЮНИТИ – ДАНА, 2003. – 237 с.
2. Колемаев В.А. Математическая экономика: Учебник для вузов.– М.: ЮНИТИ, 1998. –240 с.
3. Исследование операций в экономике: Учеб. пособие для вузов/ Под ред. проф. Н.Ш. Кремера.– М.: Банки и биржи, ЮНИТИ, 1999. – 407 с.
4. Исследование операций: основы теории и экономические приложения: Учеб. пособие.– Екатеринбург: Изд-во Урал.гос.проф.-пед.ун-та, 1996,–112 с.
5. Методические указания для выполнения контрольной работы по дисциплине "Математическое программирование" для студентов заочного обучения. – Екатеринбург, 2003.–27 с.
6. Габасов Р., Кириллова Ф.М. Методы оптимизации. -Мн.: Изд-во БГУ, 1975.– 280 с.
7.Ланкастер К. Математическая экономика.–М.: Сов. радио, 1972.
8. Методические указания для выполнения контрольной работы по дисциплине "Математическое моделирование экономических систем" для студентов заочного обучения. – Екатеринбург, 2003. –27 с.