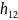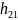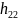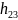- •Экзаменационные вопросы.
- •Задачи к экзамену
- •Имеются следующие данные об оценке интеллекта iq и отношении к автомобилям по выборке 190 старшекурсниц в пригородном вуЗе.
- •Порядковые шкалы. Проверка гипотезы однородности двух независимых выборок с помощью ранговых критериев (критерий числа инверсий, критерий суммы рангов).
Экзаменационные вопросы.
Основные математические структуры. Поля и кольца.
Примеры полей и колец.
Изоморфизм полей и колец.
Случайные величины и их функции распределения.
Закон распределения дискретной случайной величины. Плотность распределения непрерывной случайной величины, ее свойства.
Математическое ожидание случайной величины и его свойства.
Дисперсия случайной величины и ее свойства.
Как задается нормальное распределение? Укажите основные свойства и характеристики одномерного нормального распределения. Чем объясняется особая роль нормального распределения в статистике?
Параметры нормального распределения, их смысл.
Основной смысл центральной предельной теоремы (ЦПТ) и закона больших чисел(ЗБЧ).
Понятие асимптотической нормальности.
Система двух случайных величин. Двумерная нормальная случайная величина.
Условные законы распределения,
Условные математические ожидания и дисперсии.
Независимые случайные величины.
Понятие корреляционной зависимости случайных величин.
Функция регрессии. Линейная функция регрессии и коэффициент корреляции.
Коэффициент регрессии и его связь с коэффициентом корреляции
Регрессионный анализ. Общая задача регрессии. Что представляет собой регрессионная зависимость (регрессия) между случайными переменными? Определите дисперсию вдоль линии регрессии и «остаточную» дисперсию.
Понятия генеральной совокупности и случайной выборки.
Репрезентативность выборки.
Основные задачи математической статистики.
Задача статистического оценивания. Точечные статистические (выборочные) оценки и их свойства.
Понятие об интервальных оценках параметров распределения на примере получения доверительного интервала для математического ожидания нормально распределенной генеральной совокупности с известным стандартным отклонением σ.
Что такое статистическая гипотеза и статистический критерий? В чем суть процедуры проверки статистической гипотезы? Простая и сложная гипотезы. Общая методика проверки простых статистических гипотез. Понятия о критериях проверки.
Определите понятия критического значения, вероятностей ошибок первого и второго рода, уровня значимости и мощности критерия.
Основные задачи применения математики в психологии. Измерения в психологических и социологических исследованиях. Определите основные психологические шкалы: наименований, порядка, интервалов, отношений, и приведите примеры. Как соотносятся эти шкалы между собой? Какие способы описания выборочных данных и выборочные характеристики используются при измерениях в шкалах наименований, порядка и интервалов?
Критерий согласия
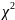 .
.
29. Критерии проверки гипотез, основанные на рангах.
30. Анализ однофакторных моделей. Критерий Краскела-Уоллиса.
Задачи к экзамену
Найти среднее значение и выборочную дисперсию по данным выборкам
Вариант1 |
|
|
|
1 |
20 |
2 |
15 |
3 |
10 |
4 |
5 |
По случайной выборке 25 детей были получены значения IQ Кульмана, при которых
 =113,64
и sx=12,40.
Используя критерий Стьюдента
=113,64
и sx=12,40.
Используя критерий Стьюдента
 =
=
,
проверить гипотезу H0
:Математическое
ожидание
 для IQ
равно 100. Какие допущения относительно
распределения генеральной совокупности
необходимо сделать, чтобы использовать
указанный критерий?
для IQ
равно 100. Какие допущения относительно
распределения генеральной совокупности
необходимо сделать, чтобы использовать
указанный критерий?
Как использовать квантили стандартных статистических распределений: хи-квадрат, Стьюдента и Фишера для вычисления границ доверительных интервалов и критических значений для критериев проверки гипотез. Приведите примеры критериев, использующих указанные распределения.
Номиинальные шкалы. Проверка гипотезы о заданном законе распределения на примере следующей задачи:
В результате опроса 100 избирателей получилось следующее распределение голосов между кандидатами А ,B и C:
A |
B |
C |
35 |
27 |
38 |
Используя критерий 2 Пирсона
 =
=
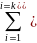
с уровнем значимости =0.05 проверить гипотезу H0 о том, что распределение вероятностей для числа голосов будет следующим:p(A)=3/8, p(B)=1/4, p(C)=3/8.
Номиинальные шкалы. Проверка гипотезы об однородности двух признаков на примере следующей задачи:
В результате опроса в двух выборках по 100 избирателей в каждой получилось следующее распределение голосов между кандидатами А ,B и C:
A |
B |
C |
35 |
27 |
38 |
34 |
26 |
40 |
Используя критерий 2 Пирсона
=
,
где

с уровнем значимости =0.05 проверить гипотезу H0 об однородности этих выборок.
Номинальные шкалы. Проверка гипотезы независимости в таблице сопряженности признаков.
Дайте описание таблицы сопряженности признаков. Расскажите о вычислении статистики «хи-квадрат» для проверки гипотезы независимости на примере решения следующей задачи:
Проводились диагностические исследования умственного развития детей одинакового возраста, обучающихся в сельских и городских школах. В эксперименте участвовало 100 человек из городских и 100 - из сельских школ. Числа h0j детей с нормальными, заниженными и завышенными уровнями умственного развития приведены в таблице.
Тип школы i |
Уровень умственного развития |
|
||
|
1-заниженный |
2-нормальный |
3-завышенный |
hi0 |
1-городская |
25= |
50= |
25= |
100 |
2-сельская |
52= |
41= |
7= |
100 |
h0j |
77 |
91 |
32 |
200 |
Проверить с помощью критерия 2
 =
n(
=
n(
, являются ли независимыми уровень умственного развития учеников и тип школы при уровне значимости 5%.